Презентация на тему: Двугранный угол. Угол между плоскостями3
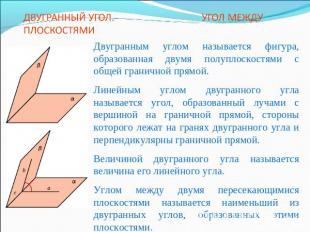
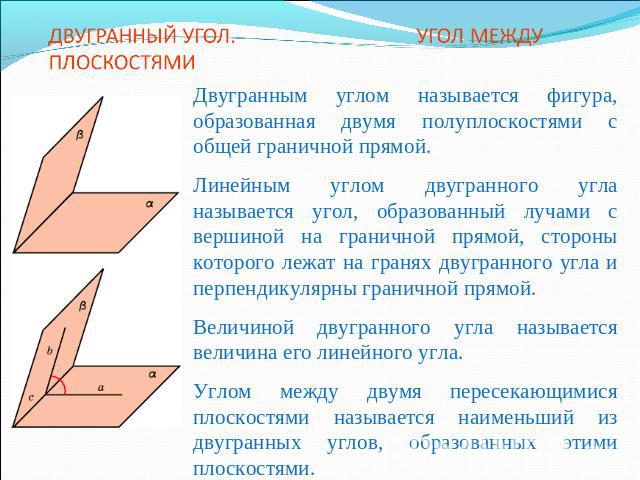
ДВУГРАННЫЙ УГОЛ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИДвугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой.Величиной двугранного угла называется величина его линейного угла.Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

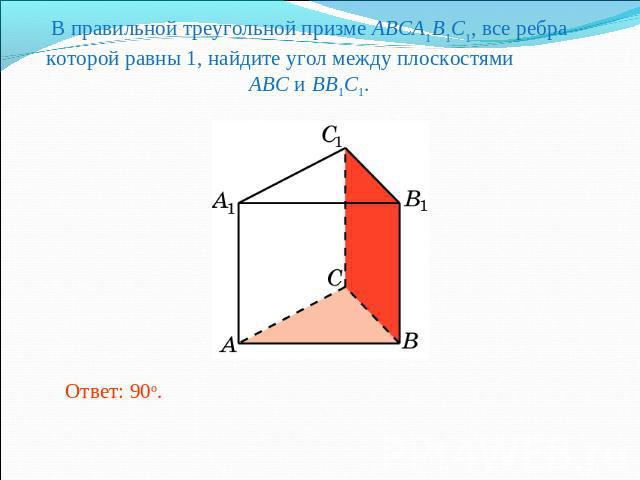
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между плоскостями ABC и BB1C1.

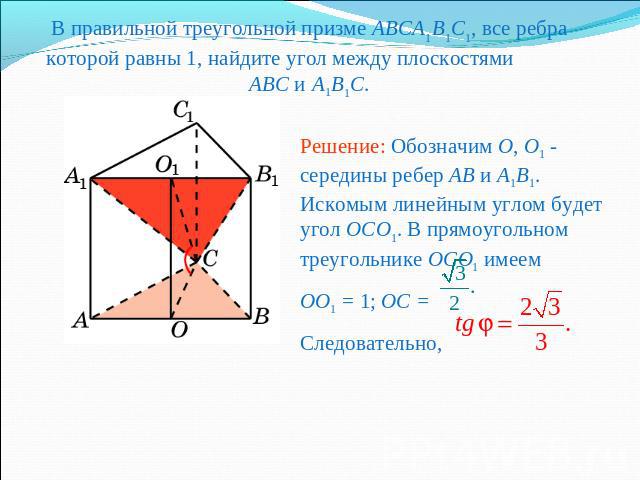
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между плоскостями ABC и A1B1C.Решение: Обозначим O, O1 - середины ребер AB и A1B1. Искомым линейным углом будет угол OCO1. В прямоугольном треугольнике OCO1 имеемOO1 = 1; OC = Следовательно,

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между плоскостями ABC и ACB1.Решение: Обозначим O - середину ребра AC. Искомым линейным углом будет угол BOB1. В прямоугольном треугольнике BOB1 имеемBB1 = 1; BO = Следовательно,
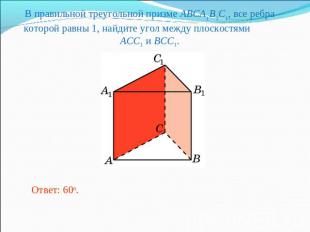
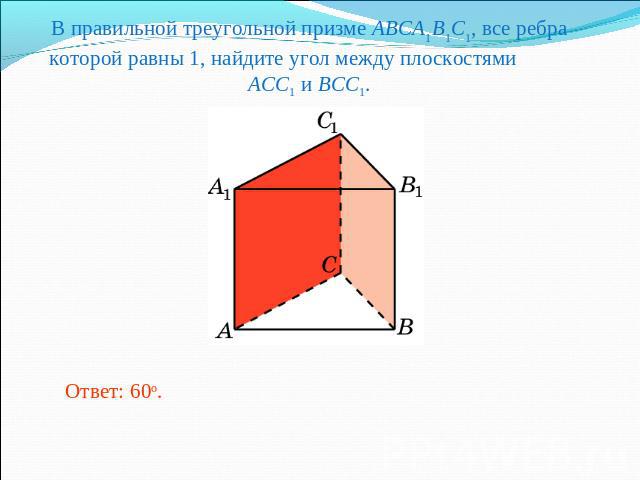
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между плоскостями ACC1 и BCC1.

В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между плоскостями ACB1 и A1C1B.Решение: Данные плоскости пересекаются по прямой DE. Обозначим G середину DE и F середину AC. Угол BGF будет искомым. В треугольнике BGF имеемBF = ; BG = FG = По теореме косинусов, имеем