Презентация на тему: Свойства равнобедренного треугольника

Свойства равнобедренного треугольника

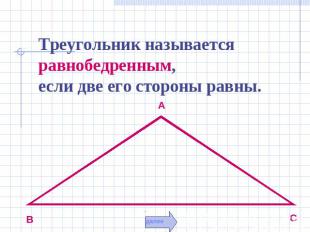
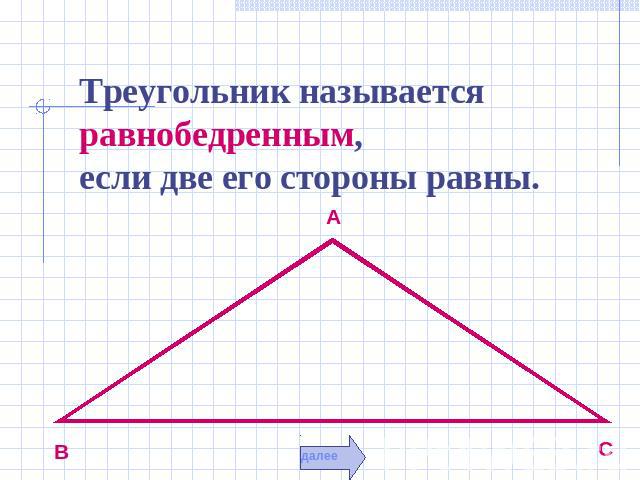
Треугольник называется равнобедренным, если две его стороны равны.

Треугольник Треугольник - самая простая замкнутая прямолинейная фигура. Это одна из первых, свойства которой человек узнал еще в глубокой древности. Эта фигура всегда имела широкое применение в практической жизни: в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей, изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах.

Треугольник Древняя Греция. Учение о треугольниках развивалось в ионийской школе, основанной в VII в. до н. э. Фалесом, и в школе Пифагора. Фалес доказал, что треугольник определяется одной стороной и двумя прилежащими к ней углами. Учение о треугольниках было затем полностью изложено в первой книге “Начал” Евклида. Среди “определений ”, которыми начинается эта книга, имеются и следующие: “Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны.” “Равнобедренный – фигура, имеющая только две равные стороны.” “Разносторонний – фигура, имеющая три неравные стороны.” Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь равносторонние, затем равнобедренные и, наконец, разносторонние треугольники.

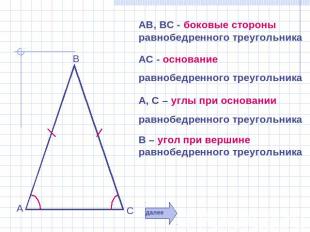
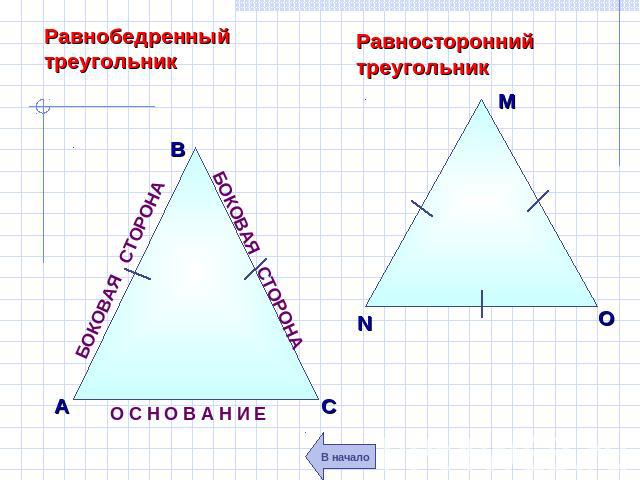
АВ, ВС - боковые стороны равнобедренного треугольника АС - основание равнобедренного треугольника А, С – углы при основании равнобедренного треугольника В – угол при вершине равнобедренного треугольника

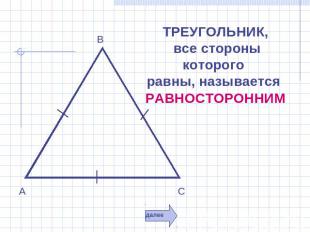
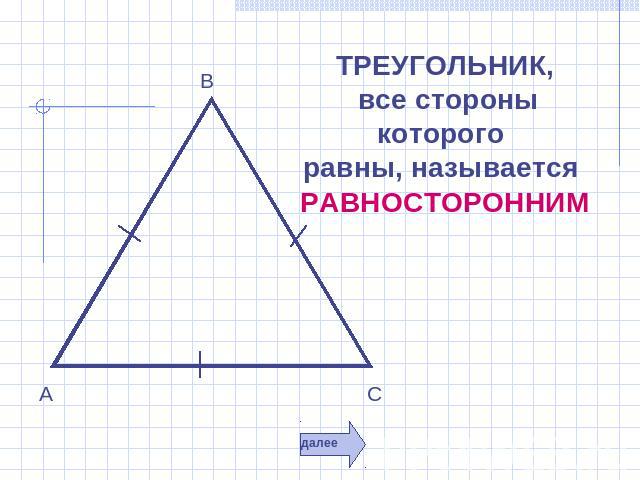
ТРЕУГОЛЬНИК, все стороны которого равны, называется РАВНОСТОРОННИМ

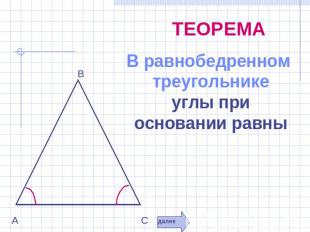
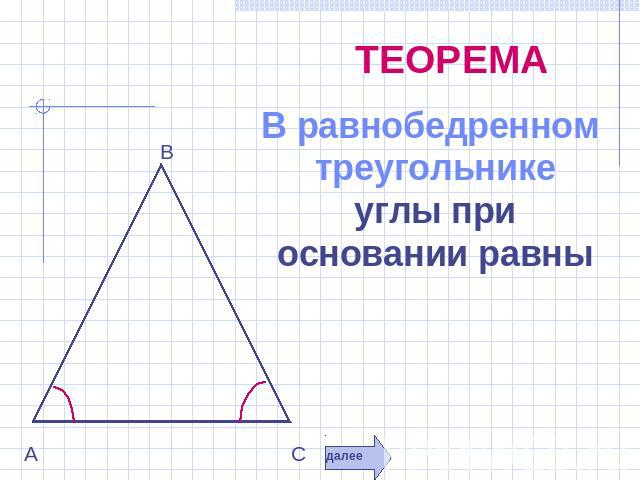
ТЕОРЕМА В равнобедренном треугольнике углы при основании равны

О равнобедренном треугольнике Равнобедренный треугольник обладает рядом геометрических свойств, которые привлекли к себе внимание еще в древности. В задачах на треугольники, содержащихся в папирусе Ахмеса, на первый план выступают равнобедренный и прямоугольный треугольники. На практике часто применялось свойство медианы равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой. Термин “медиана” происходит от латинского слова mediana- “средняя” (линия). То, что углы при основании равнобедренного треугольника равны, было известно еще древним вавилонянам 4000 лет назад.

Фалес Милетский Фалес из Милета, главного города Ионни, считается родоначальником греческой философии и науки. Как философ, он учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее в конце концов опять превращается. Историческое значение философской деятельности Фалеса заключается в том, что им был сделан решающий шаг от мифологического мировоззрения к научному материалистическому представлению о мире.

Историческая справка Фалес Милетский Почти все философы Древней Греции тщательно занимались математикой, и в частности, геометрией. Фалесу Милетскому Прокл приписывает открытие или доказательство теорем о том, что: углы при основании равнобедренного треугольника равны, диаметр делит круг пополам, вертикальные углы равны и др. Эти положения были частично известны еще вавилонянам и египтянам. Однако в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае. Родоначальник греческой философии и науки Открыл и доказал множество теорем

Историческая справка Фалес Милетский При помощи общих доказательств, с постепенным переходом от одной истины к другой, греческие математики создали геометрию как науку. Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионнийской школы, основателем которой и был Фалес.

Историческая справка Фалес Милетский Фалес сделал ряд открытий в области астрономии: установил время равнодействий и солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и и.п. Особенную славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Фалес был не только философом и ученым, но также государственным и общественным деятелем. Вот почему он был причислен к группе “семи мудрецов” древности.

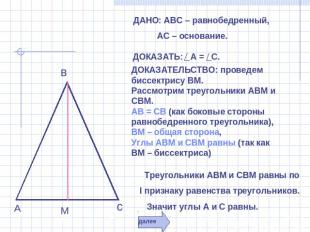
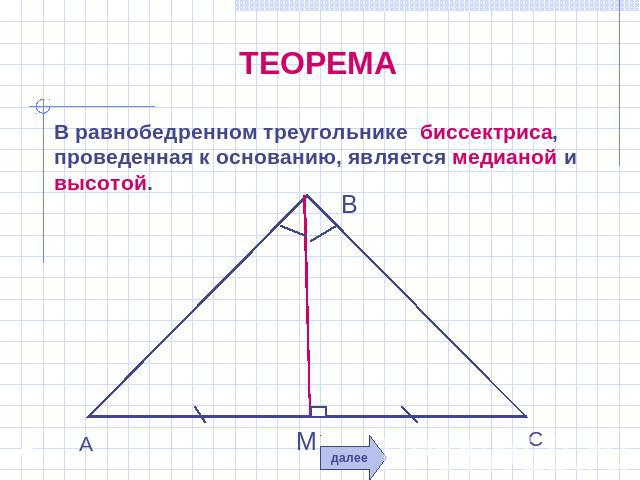
ДАНО: АВС – равнобедренный, АС – основание. ДОКАЗАТЬ: А = С. ДОКАЗАТЕЛЬСТВО: проведем биссектрису ВМ. Рассмотрим треугольники АВМ и СВМ.АВ = СВ (как боковые стороны равнобедренного треугольника),ВМ – общая сторона, Углы АВМ и СВМ равны (так как ВМ – биссектриса) Треугольники АВМ и СВМ равны по I признаку равенства треугольников. Значит углы А и С равны.

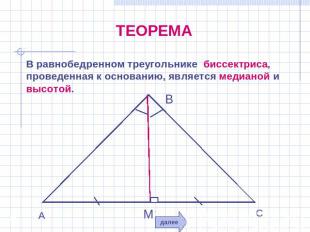
ТЕОРЕМА В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

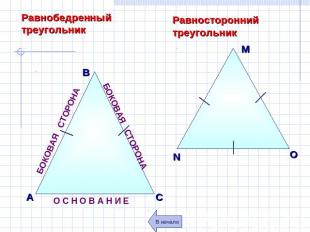
Равнобедренный треугольник Равносторонний треугольник