Презентация на тему: Двугранный угол. Угол между плоскостями
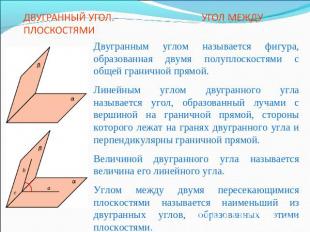
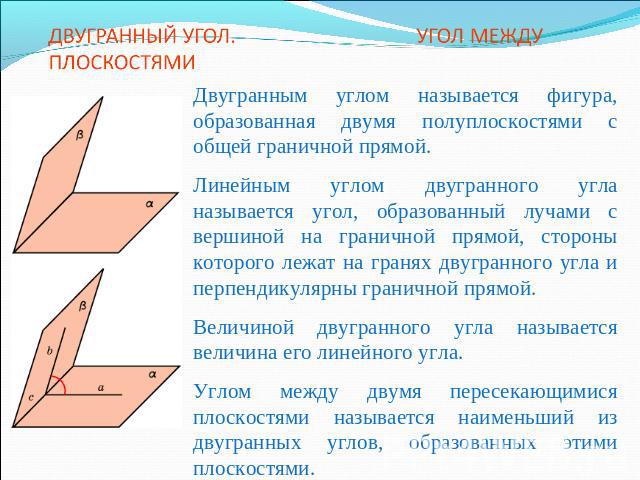
ДВУГРАННЫЙ УГОЛ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИДвугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой.Величиной двугранного угла называется величина его линейного угла.Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

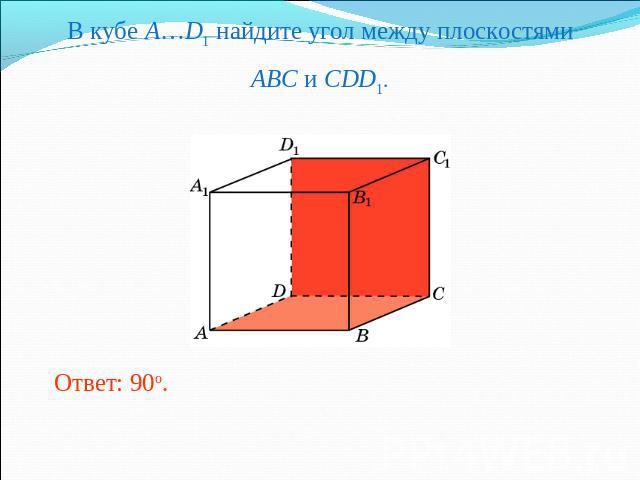
В кубе A…D1 найдите угол между плоскостямиABC и CDD1. Ответ: 90o.
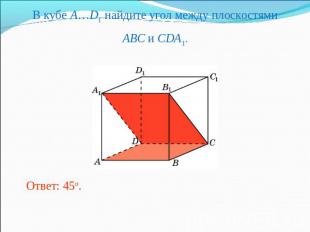
В кубе A…D1 найдите угол между плоскостямиABC и CDA1.Ответ: 45o.

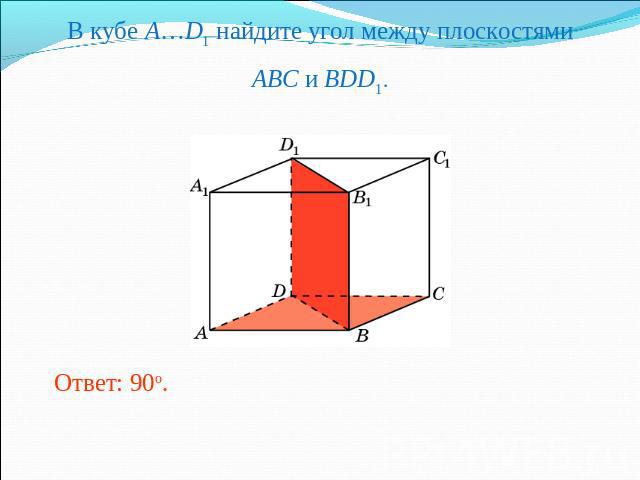
В кубе A…D1 найдите угол между плоскостямиABC и BDD1.Ответ: 90o.

В кубе A…D1 найдите угол между плоскостямиABC и BC1D.Решение: Обозначим O середину BD. Искомым линейным углом будет угол COC1. В прямоугольном треугольнике COC1 имеемCC1 = 1; CO = Следовательно,

В кубе A…D1 найдите угол между плоскостямиABC и AB1D1.Решение: Плоскость AB1D1 параллельна плоскости BC1D. Из предыдущей задачи следует, что
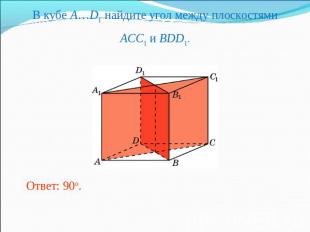
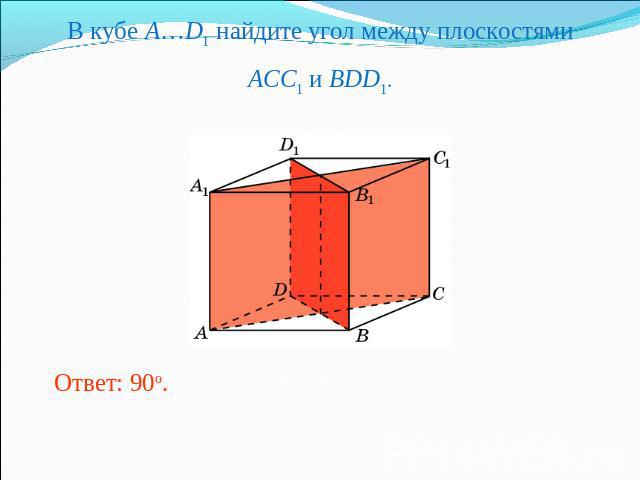
В кубе A…D1 найдите угол между плоскостямиACC1 и BDD1.

В кубе A…D1 найдите угол между плоскостямиABC1 и BB1D1. Решение: Заметим, что плоскость равностороннего треугольника ACB1 перпендикулярна диагонали BD1, которая проходит через центр O этого треугольника. Искомым линейным углом будет угол B1OE, который равен 60o.

В кубе A…D1 найдите угол между плоскостямиBC1D1 и BA1D.Решение: Заметим, что плоскость равностороннего треугольника BDA1 перпендикулярна диагонали AC1, которая проходит через центр этого треугольника. Следовательно, данные плоскости перпендикулярны. Искомый угол равен 90o.

В кубе A…D1 найдите угол между плоскостямиBC1D и BA1D.Решение: Пусть O – середина BD. Искомый угол равен углу A1OC1. Имеем Используя теорему косинусов, получим