Презентация на тему: Двугранный угол 10 класс

ДВУГРАННЫЙ УГОЛ Учитель математики ГОУ СОШ №10 Еременко М.А.

Основные задачи урока: Ввести понятие двугранного угла и его линейного угла Рассмотреть задачи на применение этих понятий
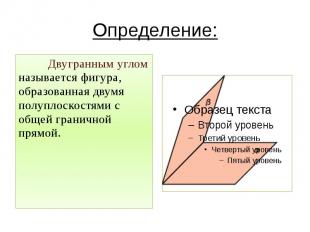
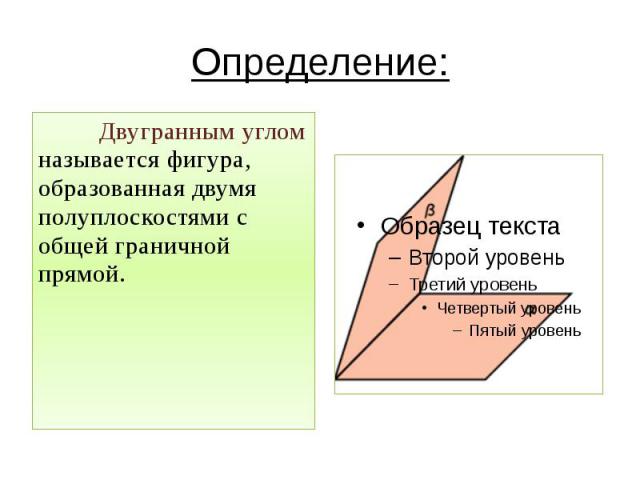
Определение: Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой.
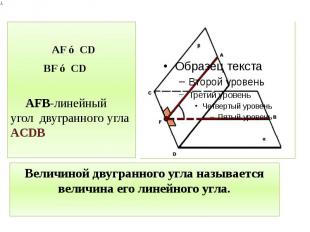
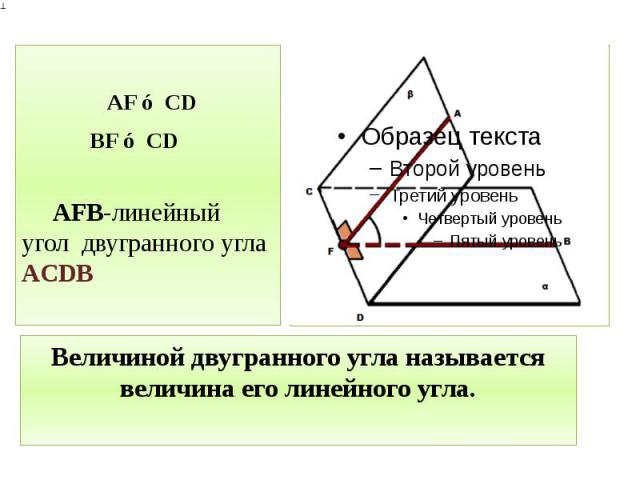
Величиной двугранного угла называется величина его линейного угла. AF ⊥ CD BF ⊥ CD AFB-линейный угол двугранного угла ACDВ
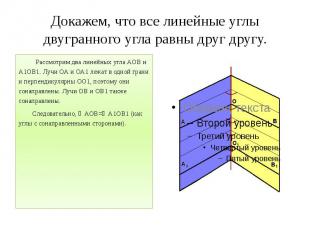
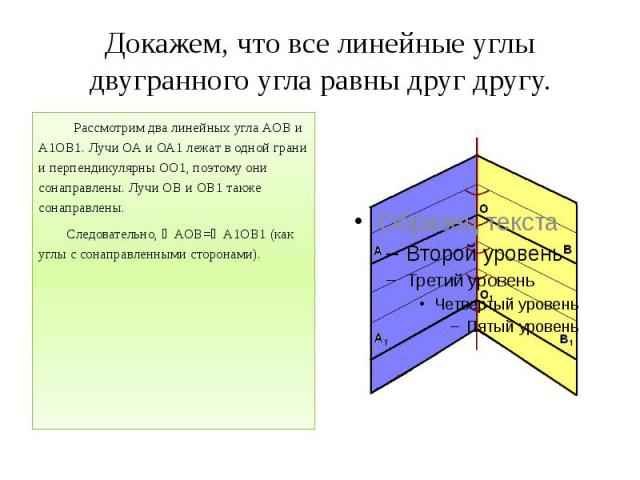
Докажем, что все линейные углы двугранного угла равны друг другу. Рассмотрим два линейных угла АОВ и А1ОВ1. Лучи ОА и ОА1 лежат в одной грани и перпендикулярны ОО1, поэтому они сонаправлены. Лучи ОВ и ОВ1 также сонаправлены. Следовательно, ∠АОВ=∠А1ОВ1 (как углы с сонаправленными сторонами).
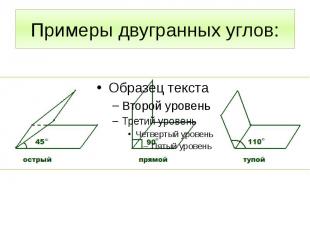
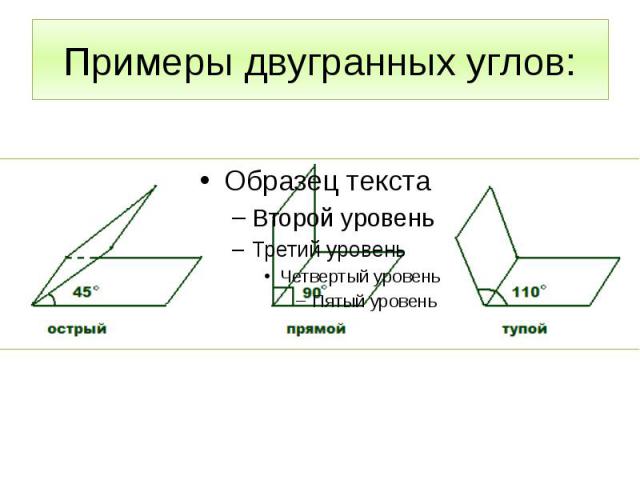
Примеры двугранных углов:
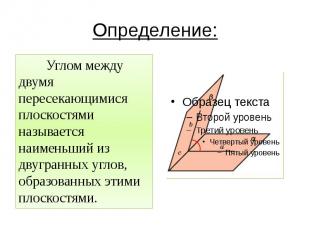
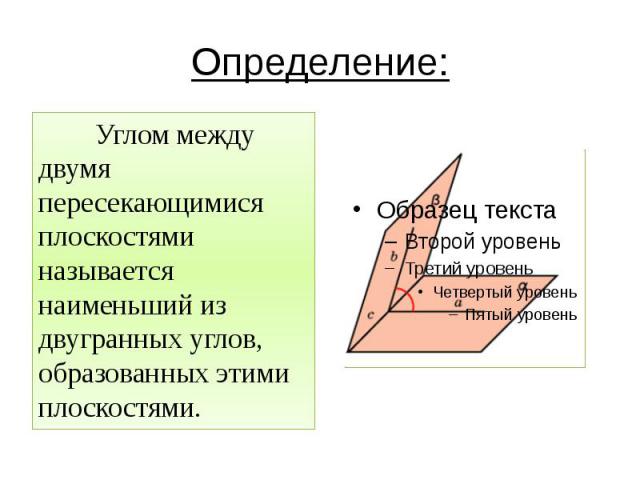
Определение: Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
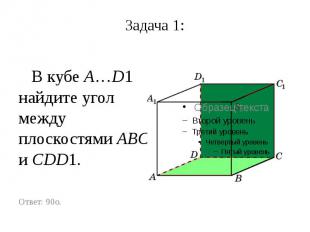
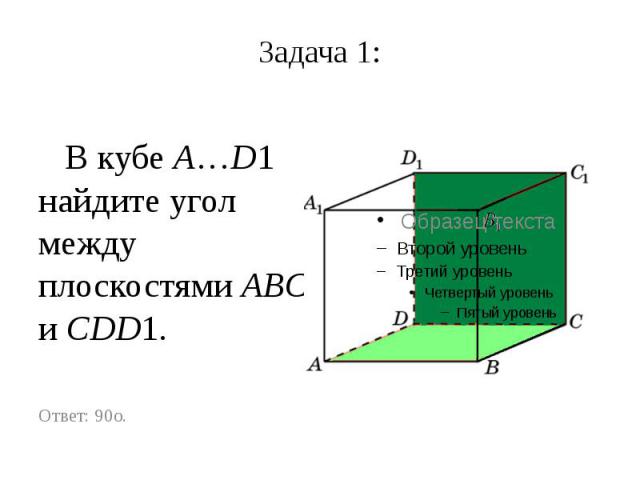
Задача 1: В кубе A…D1 найдите угол между плоскостями ABC и CDD1.
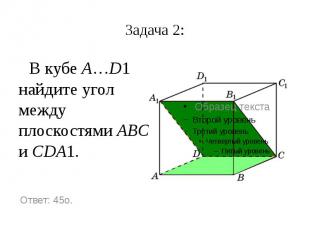
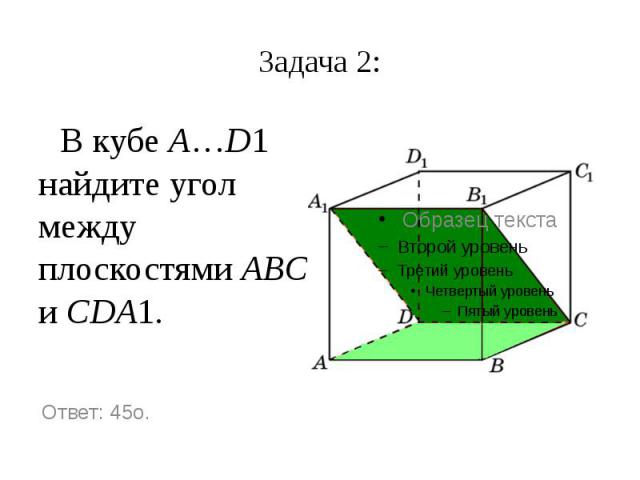
Задача 2: В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
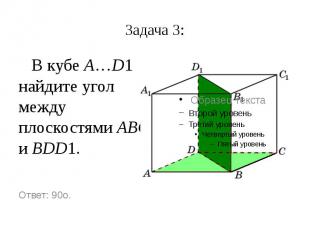
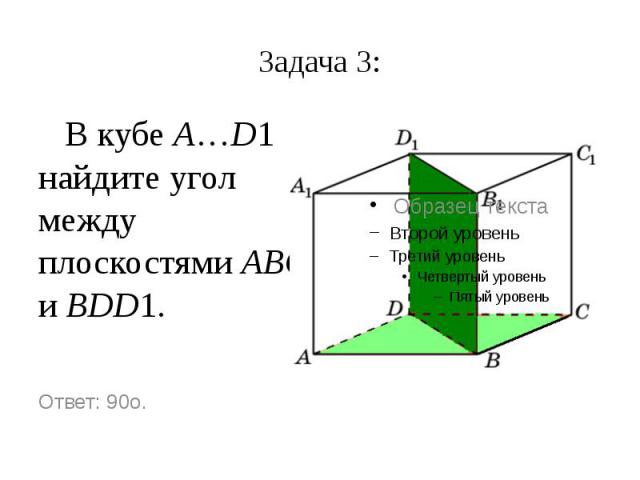
Задача 3: В кубе A…D1 найдите угол между плоскостями ABC и BDD1.

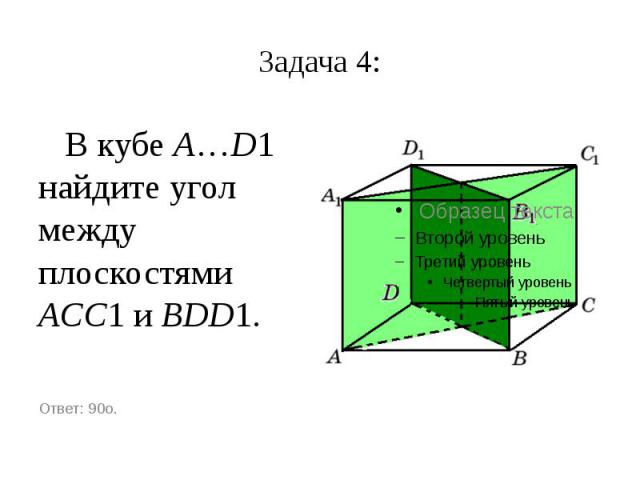
Задача 4: В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
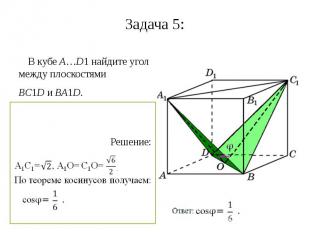
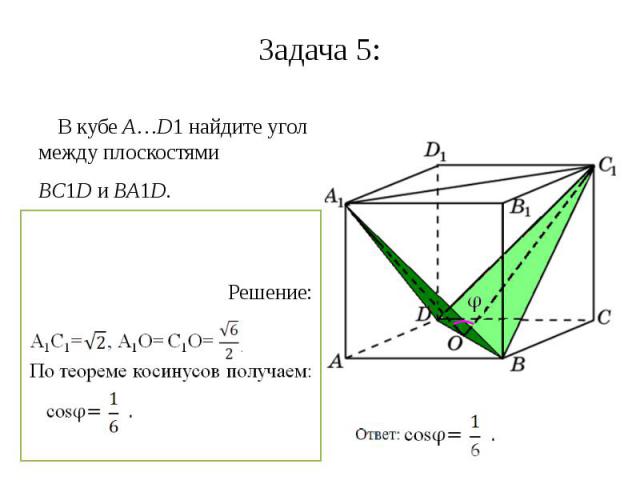
Задача 5: В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.

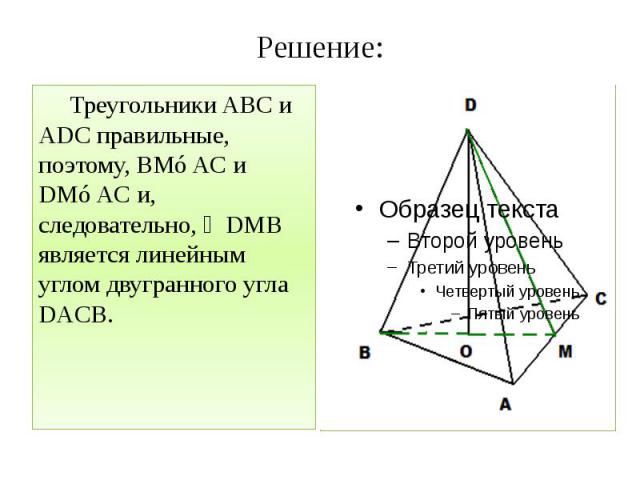
Задача 6: В тетраэдре DABC все ребра равны, точка М – середина ребра АС. Докажите, что ∠DMB – линейный угол двугранного угла BACD.
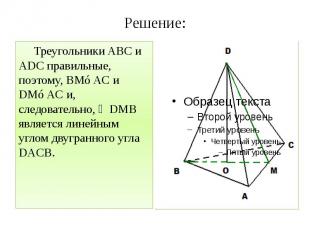
Решение: Треугольники ABC и ADC правильные, поэтому, BM⊥AC и DM⊥AC и, следовательно, ∠DMB является линейным углом двугранного угла DACB.

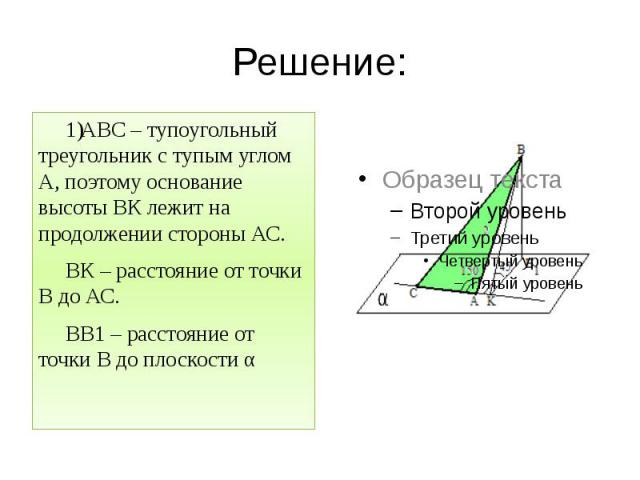
Задача 7: Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ1 равен 450.
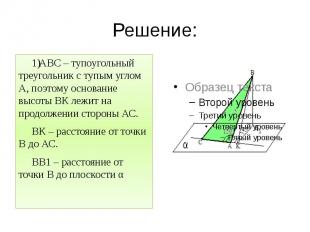
Решение: АВС – тупоугольный треугольник с тупым углом А, поэтому основание высоты ВК лежит на продолжении стороны АС. ВК – расстояние от точки В до АС. ВВ1 – расстояние от точки В до плоскости α
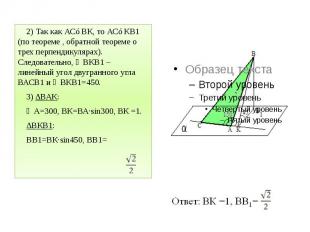
2) Так как АС⊥ВК, то АС⊥КВ1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ1 – линейный угол двугранного угла ВАСВ1 и ∠ВКВ1=450. 2) Так как АС⊥ВК, то АС⊥КВ1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ1 – линейный угол двугранного угла ВАСВ1 и ∠ВКВ1=450. 3) ∆ВАК: ∠А=300, ВК=ВА·sin300, ВК =1. ∆ВКВ1: ВВ1=ВК·sin450, ВВ1=

Домашнее задание: Параграф 3, п.22, №167, 169, с.57, вопросы 7-10.