Презентация на тему: Двугранный угол. Угол между плоскостями4
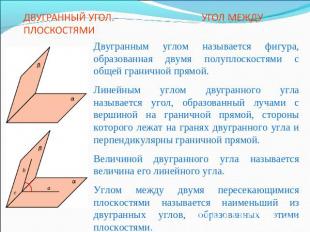
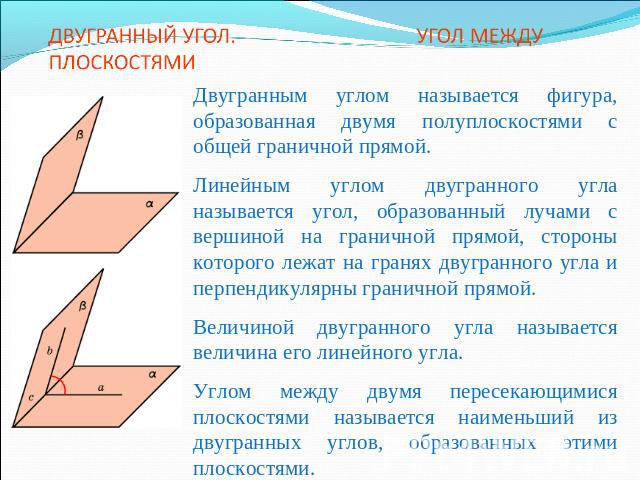
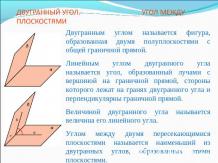
ДВУГРАННЫЙ УГОЛ. УГОЛ МЕЖДУ ПЛОСКОСТЯМИДвугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой.Величиной двугранного угла называется величина его линейного угла.Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
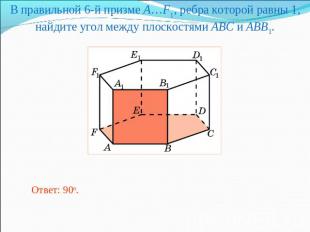
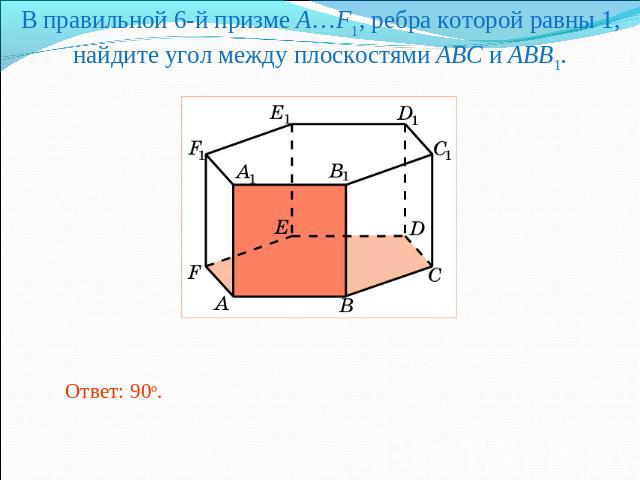
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и ABB1.

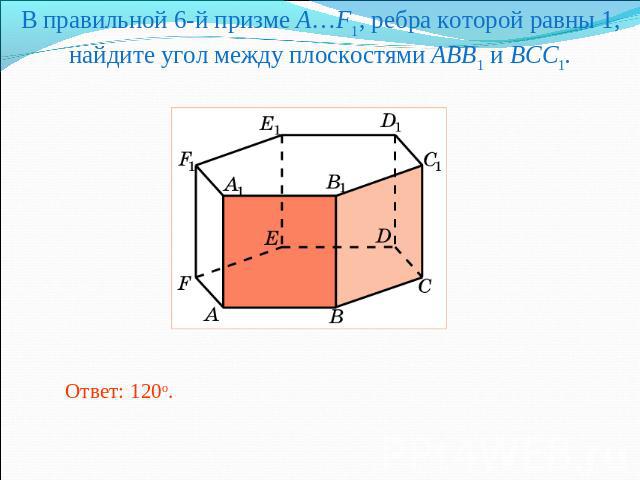
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABB1 и BCC1.
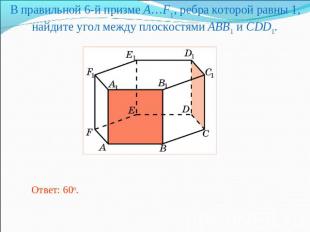
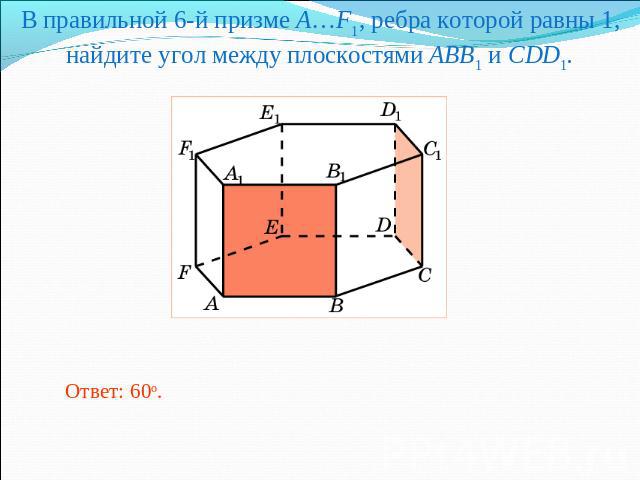
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABB1 и CDD1.
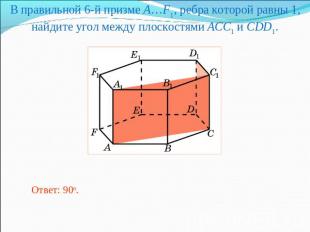
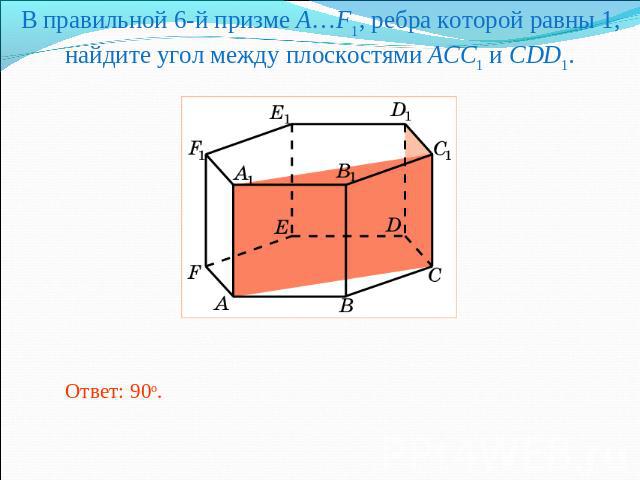
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ACC1 и CDD1.
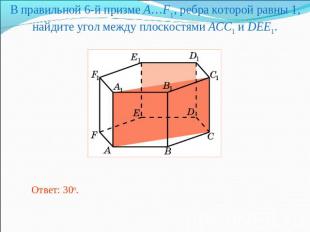
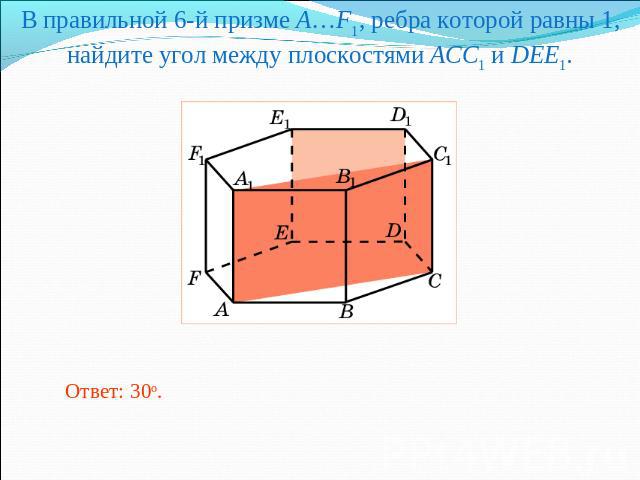
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ACC1 и DEE1.
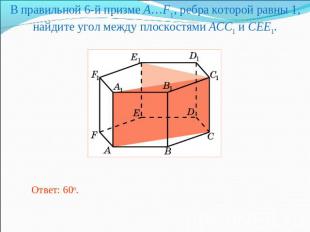
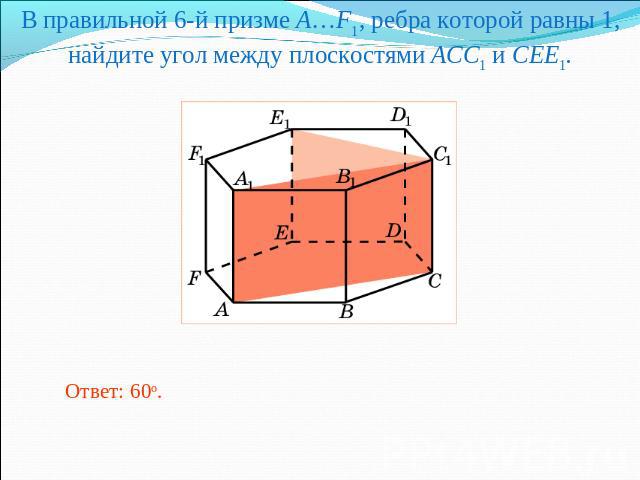
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ACC1 и CEE1.

В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и BCD1.Решение: Искомый угол равен углу O1GO, где O, O1 – центры оснований призмы, G – середина BC. В прямоугольном треугольнике O1GO имеем: OO1 = 1, OG = . Следовательно,

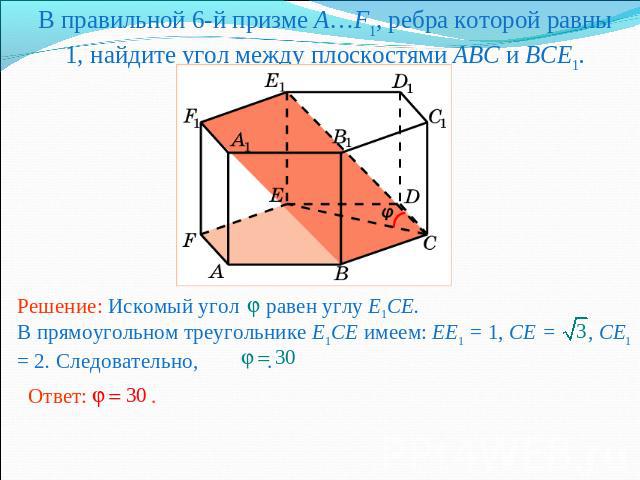
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и BCE1.Решение: Искомый угол равен углу E1CE.В прямоугольном треугольнике E1CE имеем: EE1 = 1, CE = , CE1 = 2. Следовательно, .

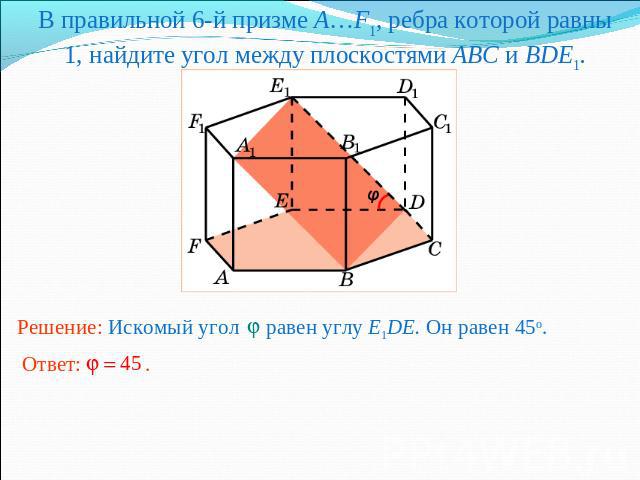
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и BDE1.Решение: Искомый угол равен углу E1DE. Он равен 45о.

В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и BDF1.Решение: Искомый угол равен углу F1GF, где G – середина BD. В прямоугольном треугольнике F1GF имеем: FF1 = 1, FG = Следовательно,

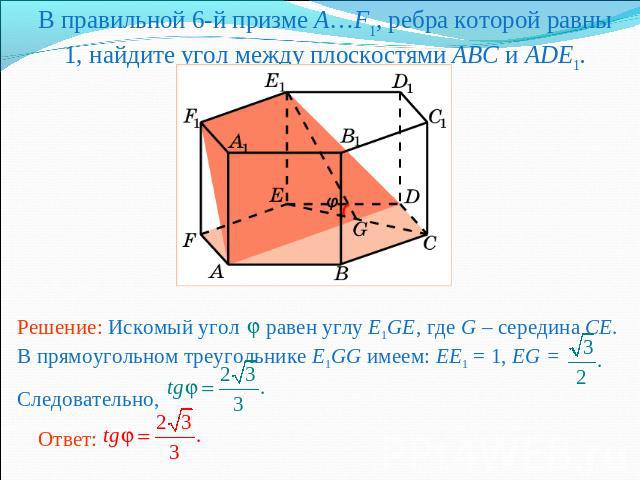
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABC и ADE1.Решение: Искомый угол равен углу E1GE, где G – середина CE. В прямоугольном треугольнике E1GG имеем: EE1 = 1, EG = Следовательно,

В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями CDE1 и AFE1.Решение: Пусть O, O1 – центры оснований призмы, P, Q – середины ребер AF и CD. Искомый угол равен углу PO1Q. В треугольнике PO1Q имеем: PO1 = QO1 = , PQ = Из теоремы косинусов получаем

В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями CDF1 и AFD1.Решение: Пусть O – центр призмы, G, G1 – середины ребер CD и C1D1. Искомый угол равен углу GOG1. В треугольнике GOG1 имеем: GG1 = GO = G1O = 1. Следовательно, = 60о.

В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между плоскостями BCD1 и AFE1.Решение: Пусть O, O1 – центры боковой грани и верхнего основания призмы. Искомый угол равен углу A1GB1, где G – середина OO1. В треугольнике A1GB1 имеем: A1B1 = 1, A1G = B1G = Из теоремы косинусов получаем