Презентация на тему: Расстояние между прямыми в пространстве

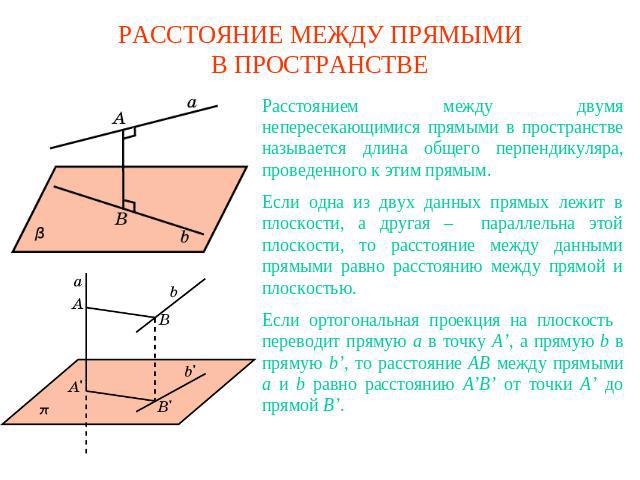
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИВ ПРОСТРАНСТВЕРасстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым. Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.Если ортогональная проекция на плоскость переводит прямую a в точку A’, а прямую b в прямую b’, то расстояние AB между прямыми a и b равно расстоянию A’B’ от точки A’ до прямой B’.
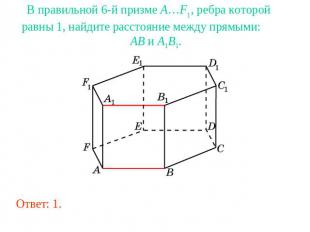
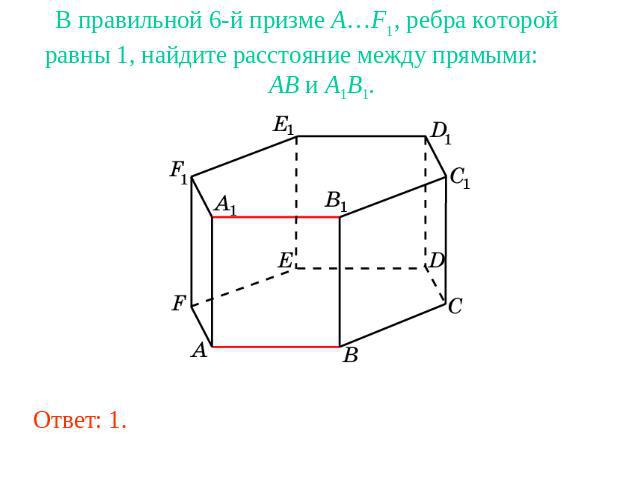
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB и A1B1.
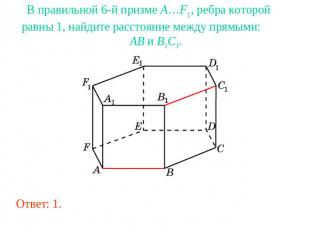
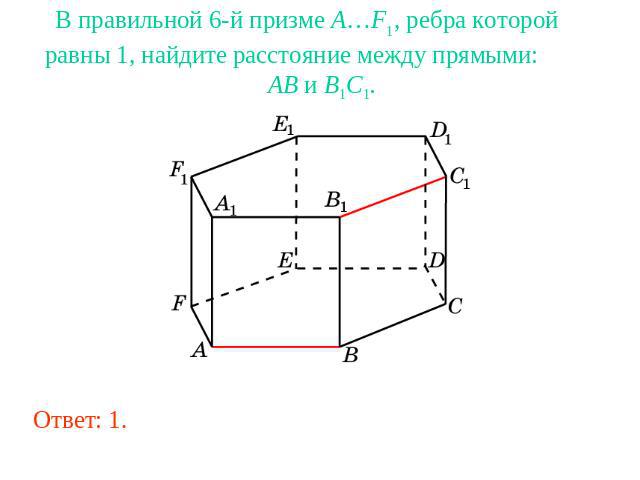
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB и B1C1.
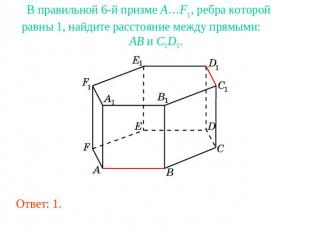
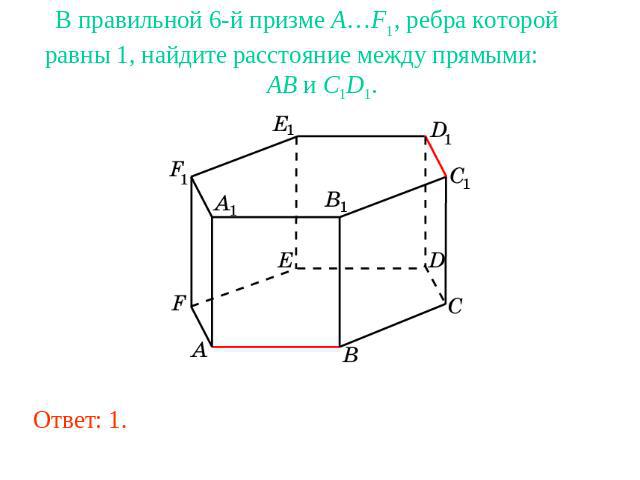
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB и C1D1.
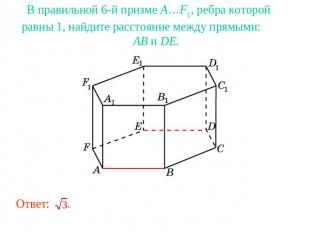
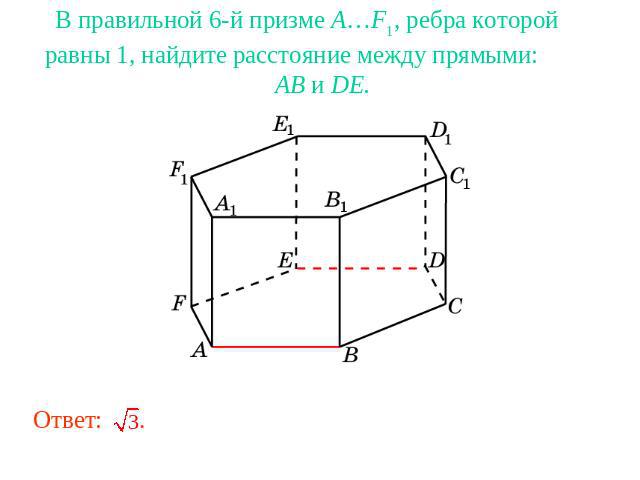
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB и DE.
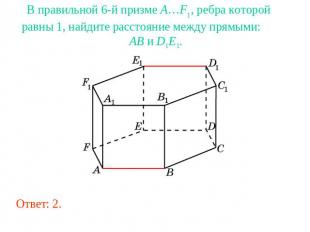
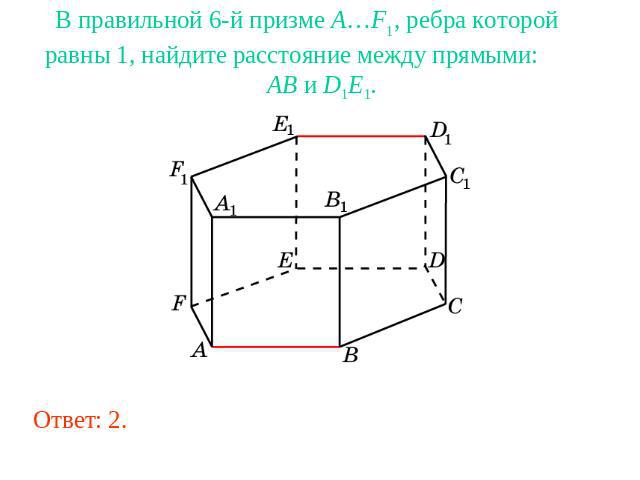
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB и D1E1.
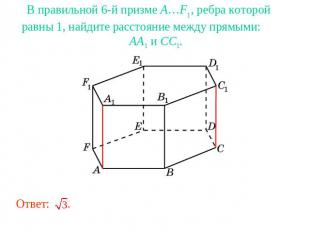
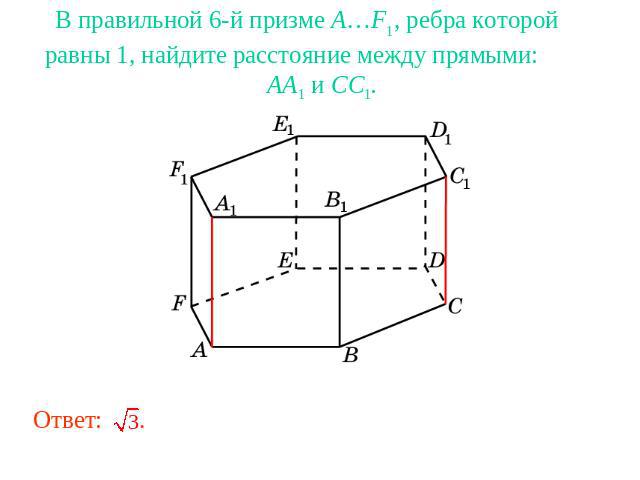
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CC1.
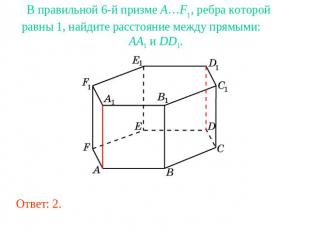
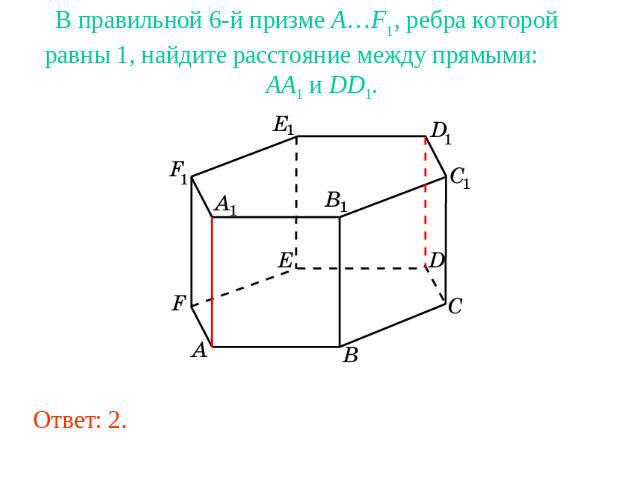
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и DD1.
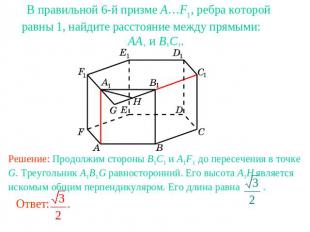
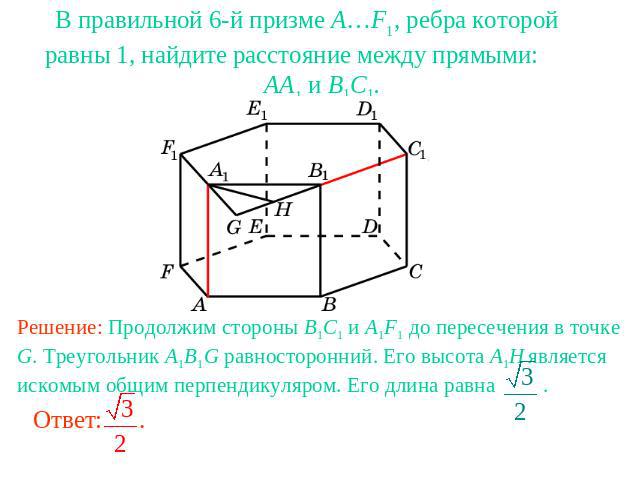
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и B1C1.Решение: Продолжим стороны B1C1 и A1F1 до пересечения в точке G. Треугольник A1B1G равносторонний. Его высота A1H является искомым общим перпендикуляром. Его длина равна .
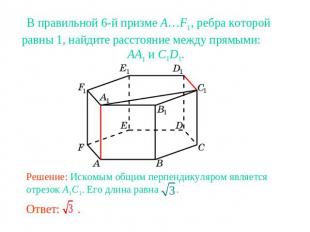
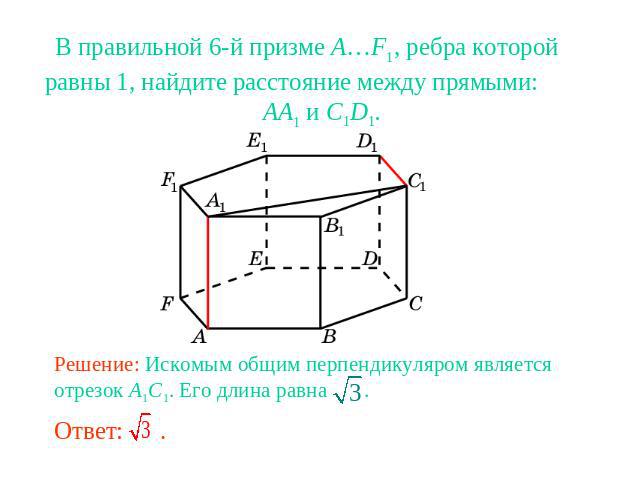
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и C1D1.Решение: Искомым общим перпендикуляром является отрезок A1C1. Его длина равна .
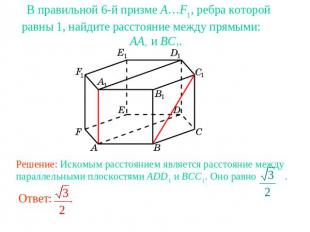
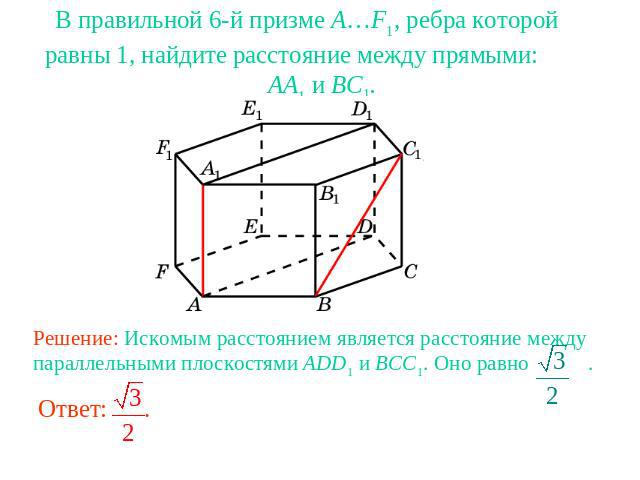
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BC1.Решение: Искомым расстоянием является расстояние между параллельными плоскостями ADD1 и BCC1. Оно равно .

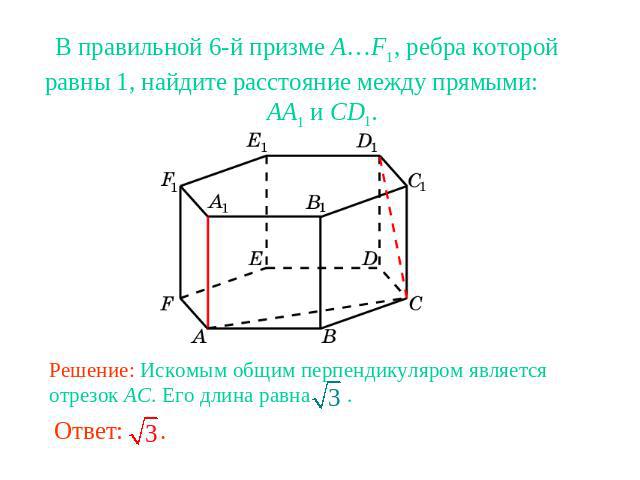
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CD1.Решение: Искомым общим перпендикуляром является отрезок AC. Его длина равна .
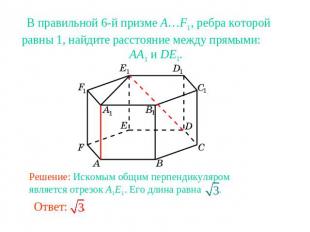
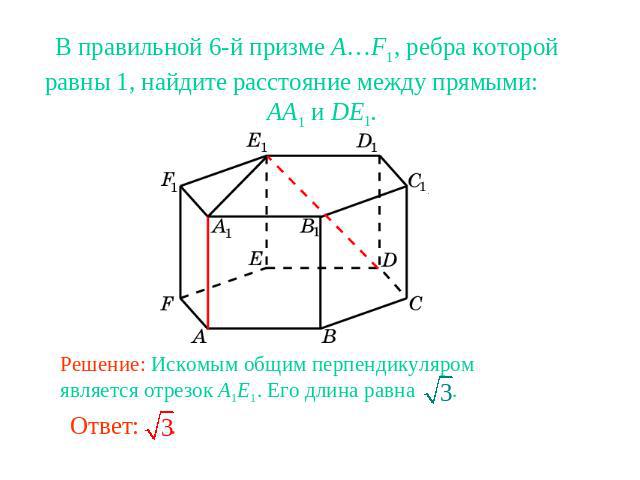
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и DE1.Решение: Искомым общим перпендикуляром является отрезок A1E1. Его длина равна .
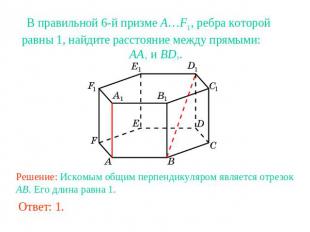
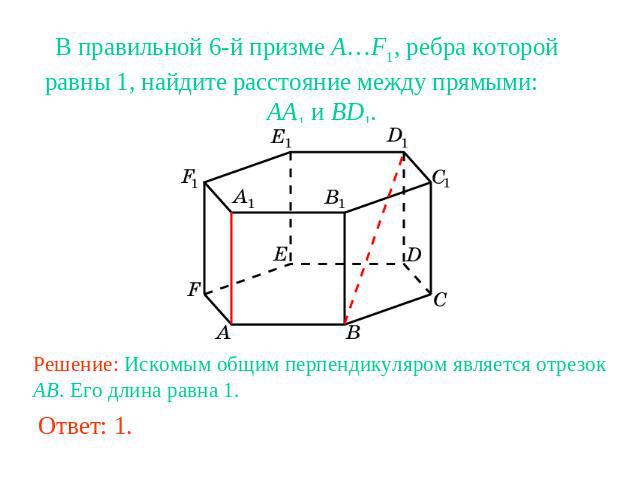
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BD1.Решение: Искомым общим перпендикуляром является отрезок AB. Его длина равна 1.
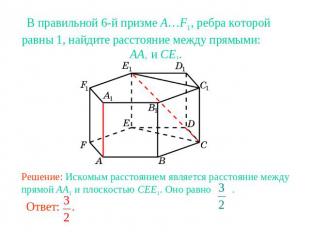
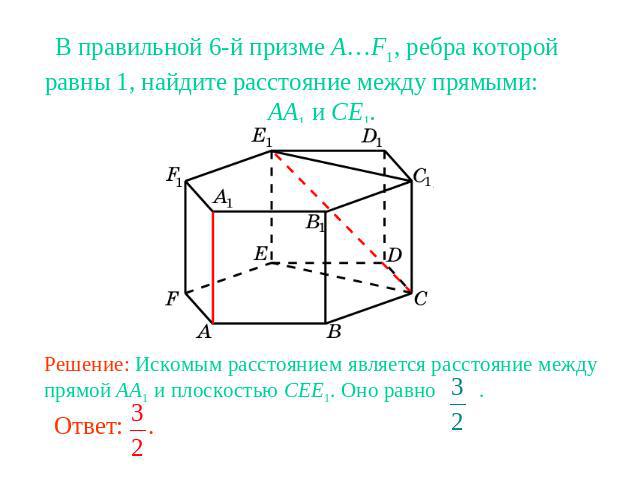
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CE1.Решение: Искомым расстоянием является расстояние между прямой AA1 и плоскостью CEE1. Оно равно .
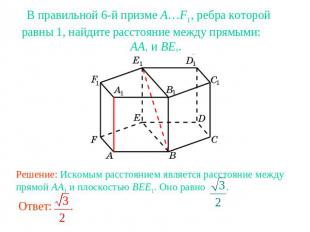
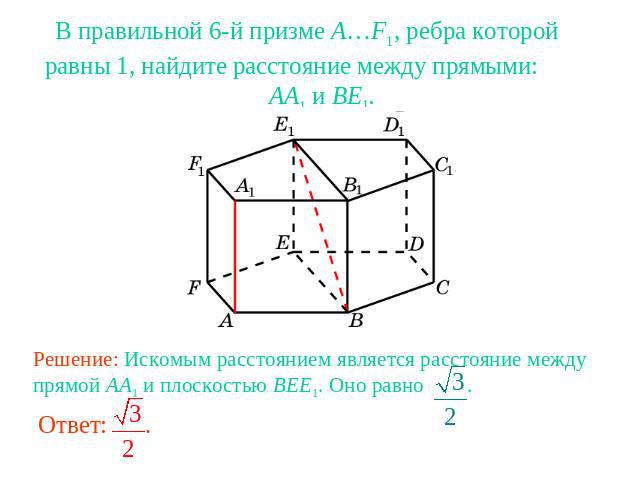
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BE1.Решение: Искомым расстоянием является расстояние между прямой AA1 и плоскостью BEE1. Оно равно .
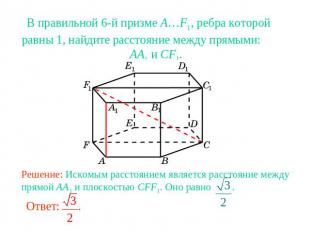
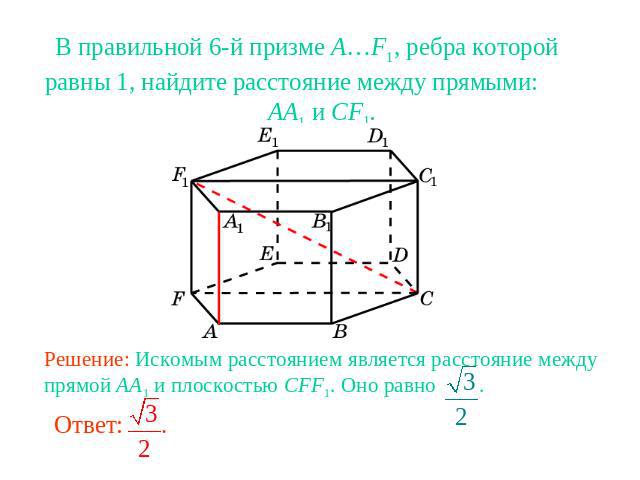
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CF1.Решение: Искомым расстоянием является расстояние между прямой AA1 и плоскостью CFF1. Оно равно .
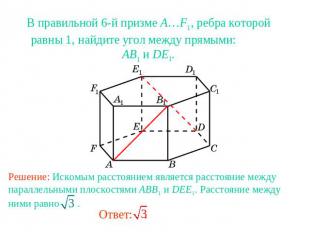
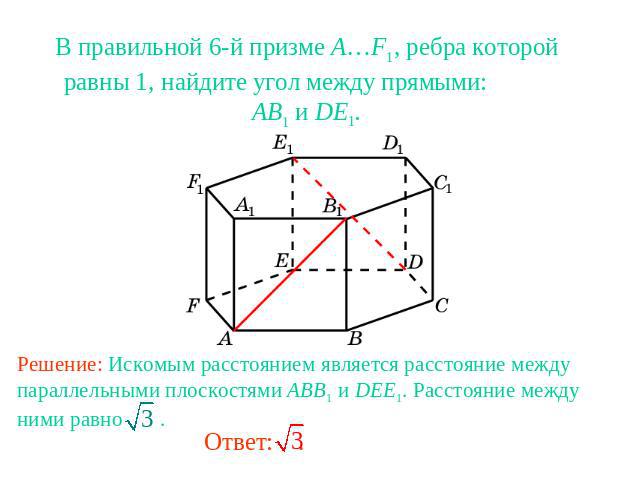
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DE1.Решение: Искомым расстоянием является расстояние между параллельными плоскостями ABB1 и DEE1. Расстояние между ними равно .
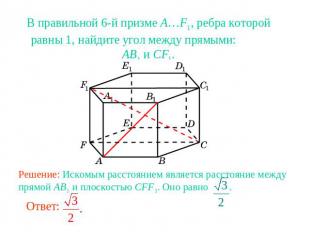
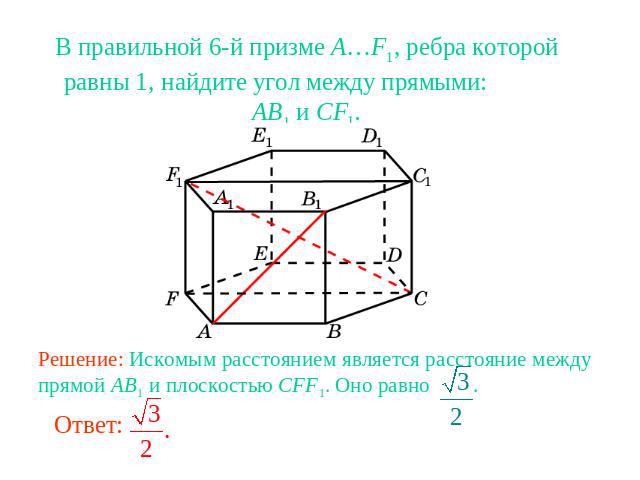
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CF1.Решение: Искомым расстоянием является расстояние между прямой AB1 и плоскостью CFF1. Оно равно .

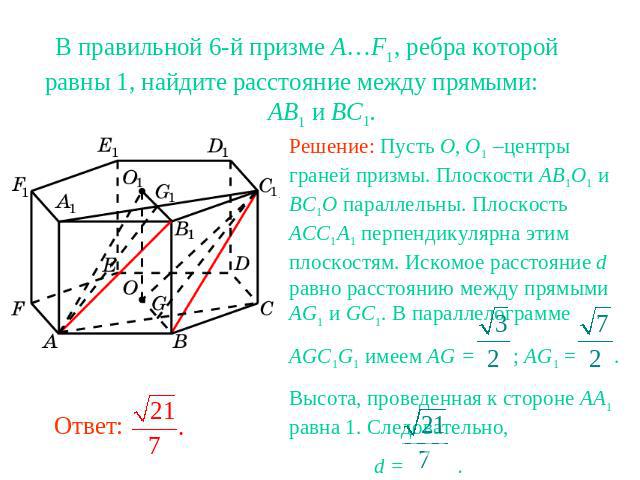
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BC1.Решение: Пусть O, O1 –центры граней призмы. Плоскости AB1O1 и BC1O параллельны. Плоскость ACC1A1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG1 и GC1. В параллелограмме AGC1G1 имеем AG = ; AG1 = . Высота, проведенная к стороне AA1 равна 1. Следовательно, d = .
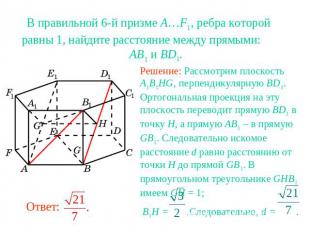
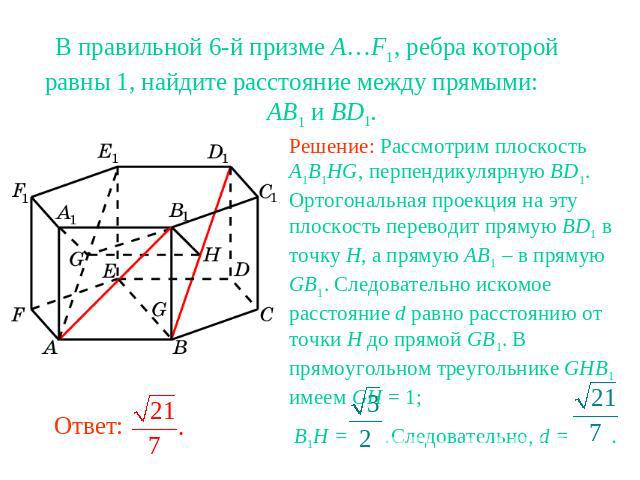
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BD1.Решение: Рассмотрим плоскость A1B1HG, перпендикулярную BD1. Ортогональная проекция на эту плоскость переводит прямую BD1 в точку H, а прямую AB1 – в прямую GB1. Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB1. В прямоугольном треугольнике GHB1 имеем GH = 1; B1H = .Следовательно, d = .
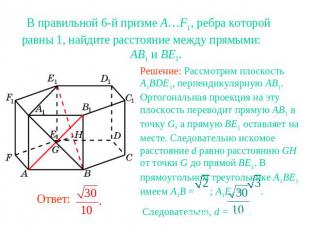
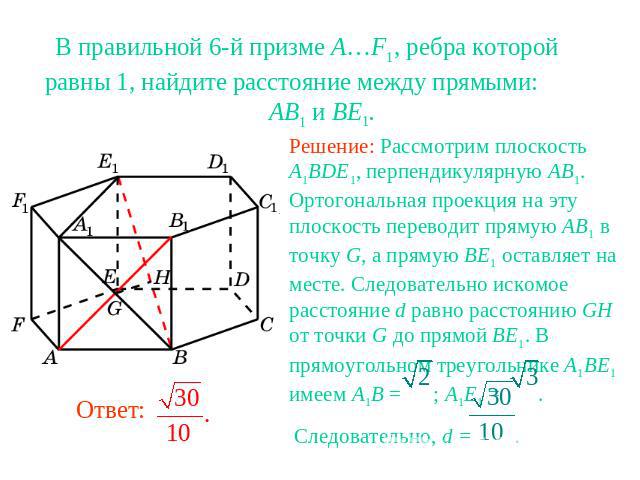
В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BE1.Решение: Рассмотрим плоскость A1BDE1, перпендикулярную AB1. Ортогональная проекция на эту плоскость переводит прямую AB1 в точку G, а прямую BE1 оставляет на месте. Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE1. В прямоугольном треугольнике A1BE1 имеем A1B = ; A1E1 = . Следовательно, d = .