Презентация на тему: Двугранный угол. Признак перпендикулярности двух плоскостей

Двугранный угол.Признак перпендикулярности двух плоскостей

Двугранный угол. Определение: Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Прямая a - ребро, полуплоскости, образующие двугранный угол называют гранями

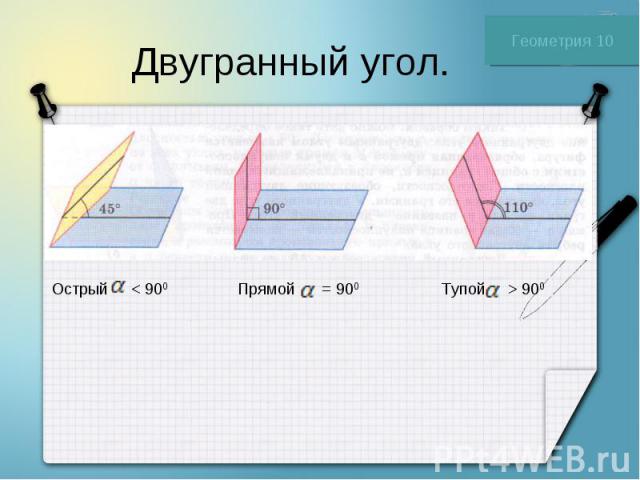
Двугранный угол.

Двугранный угол.

Признак перпендикулярности двух плоскостей Верно ли, что угол АВС линейный угол двугранного угла, если АВ и АС перпендикулярны к его ребру?Верно ли, что угол ВАС линейный угол двугранного угла, если АВ и АС лежат в гранях двугранного угла?Верно ли, что угол ВАС линейный угол двугранного угла, если АВ и АС перпендикулярны к его ребру, а точки В и С лежат на гранях двугранного угла?4.Линейный угол двугранного угла равен 800. Найдётся ли в одной из граней угла прямая перпендикулярная другой грани?5.Угол АВС линейный угол двугранного угла с ребром a, Перпендикулярна ли прямая a плоскости АВС?6.Верно ли, что все прямые, перпендикулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости?

Признак перпендикулярности двух плоскостей Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.

Признак перпендикулярности двух плоскостей Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит

Признак перпендикулярности двух плоскостей При решении задач используют следующие утверждения Следствие: Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. Перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.

Самостоятельно 1. ABCD – тетраэдр, DC=8 см, CB=6 см, AD перпендикулярен плоскости АВС,угол DCB равен 900, угол DBA равен 450. Найдите AD.2. МABC – тетраэдр, МA перпендикулярен плоскости АВС, МC=4 см, CB =6 см,Угол CAB равен 1200, AC=AB.Найти МA, угол МBC

Домашнее задание:П. 23№ 167, 170 – двугранный угол № 173, 174 – перпендикулярность плоскостей П. 24,25 № 168, 175