Презентация на тему: Расстояние от точки до плоскости в пространстве

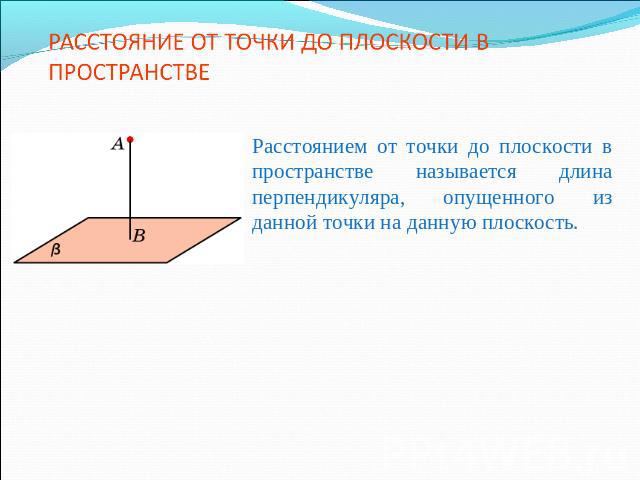
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ В ПРОСТРАНСТВЕ Расстоянием от точки до плоскости в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость.

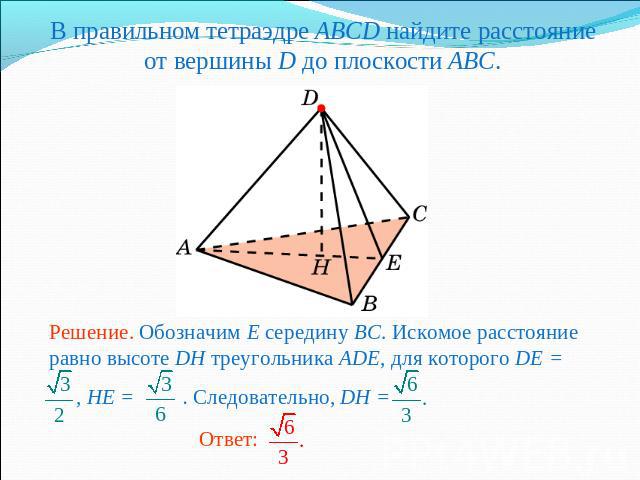
В правильном тетраэдре ABCD найдите расстояние от вершины D до плоскости ABC. Решение. Обозначим E середину BC. Искомое расстояние равно высоте DH треугольника ADE, для которого DE = , HE = . Следовательно, DH =
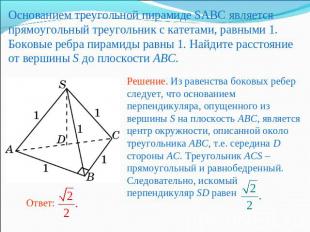
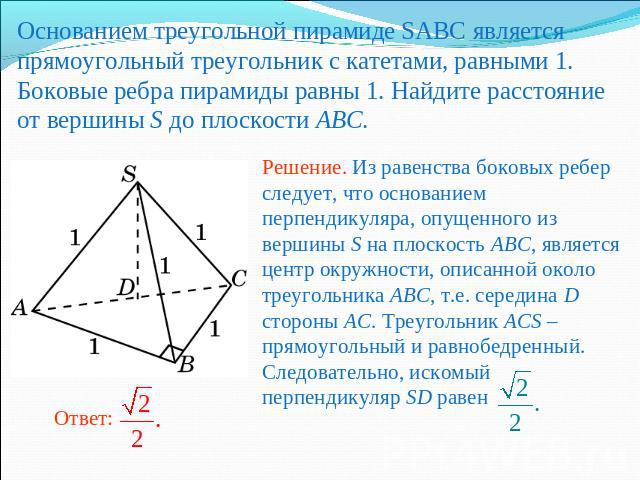
Основанием треугольной пирамиде SABC является прямоугольный треугольник с катетами, равными 1. Боковые ребра пирамиды равны 1. Найдите расстояние от вершины S до плоскости ABC.Решение. Из равенства боковых ребер следует, что основанием перпендикуляра, опущенного из вершины S на плоскость ABC, является центр окружности, описанной около треугольника ABC, т.е. середина D стороны AC. Треугольник ACS – прямоугольный и равнобедренный. Следовательно, искомый перпендикуляр SD равен
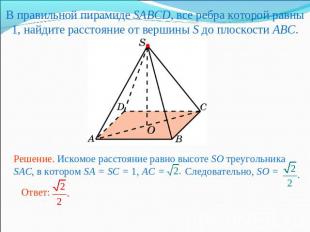
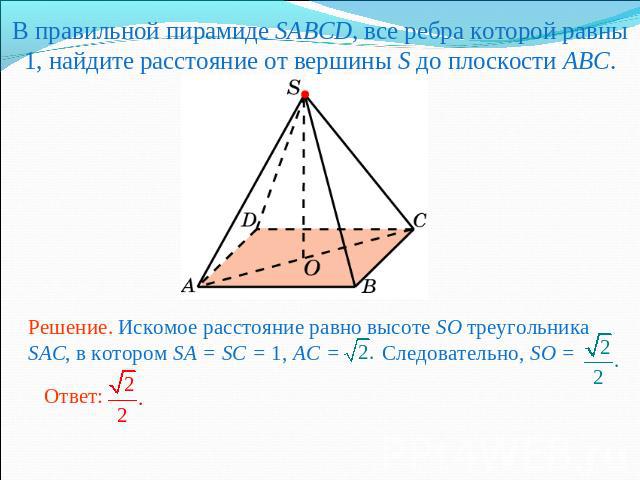
В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от вершины S до плоскости ABC.Решение. Искомое расстояние равно высоте SO треугольника SAC, в котором SA = SC = 1, AC = Следовательно, SO =

В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SBC.Решение. Обозначим E, F – середины ребер AD, BC. Искомое расстояние равно высоте EH треугольника SEF, в котором SE = SF = , EF = 1. Откуда, EH =
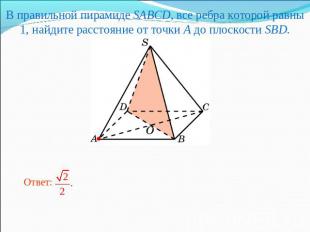
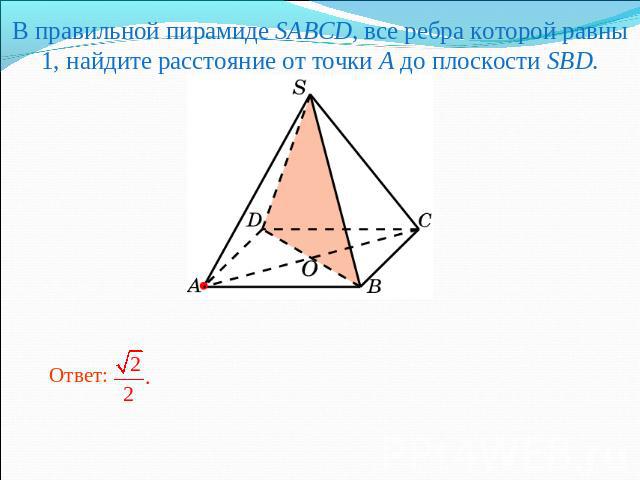
В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки A до плоскости SBD.
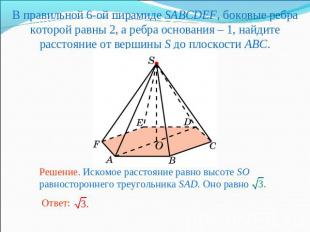
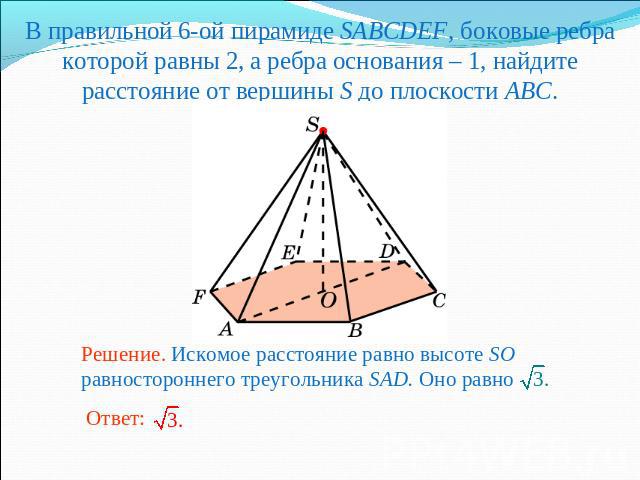
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от вершины S до плоскости ABC.Решение. Искомое расстояние равно высоте SO равностороннего треугольника SAD. Оно равно

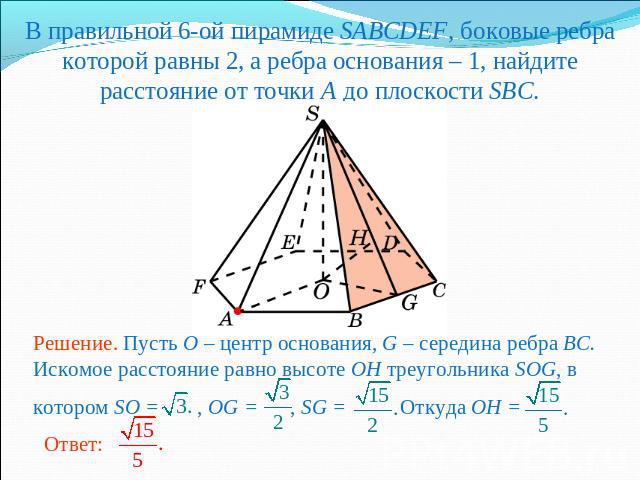
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBC.Решение. Пусть O – центр основания, G – середина ребра BC. Искомое расстояние равно высоте OH треугольника SOG, в котором SO = , OG = , SG = Откуда OH =

В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SCD.Решение. Пусть P, Q – середины ребер AF, CD. Искомое расстояние равно высоте PH треугольника SPQ, в котором PQ = SO = , SP = SQ = . Откуда PH =

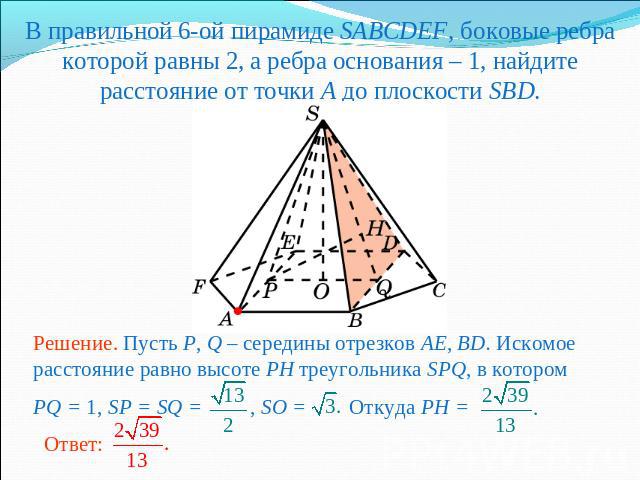
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBD.Решение. Пусть P, Q – середины отрезков AE, BD. Искомое расстояние равно высоте PH треугольника SPQ, в котором PQ = 1, SP = SQ = , SO = Откуда PH =

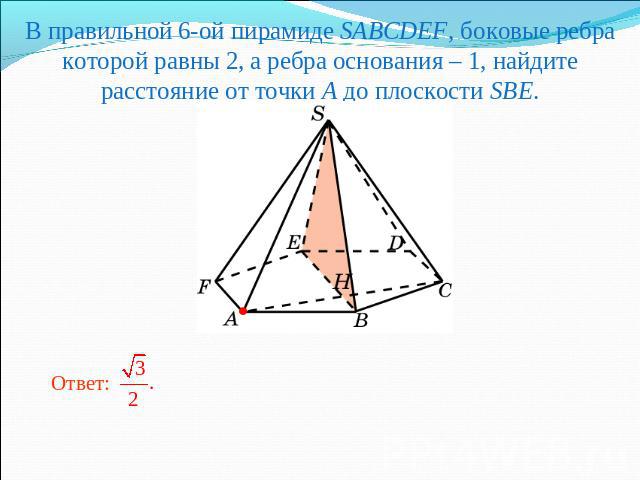
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SBE.

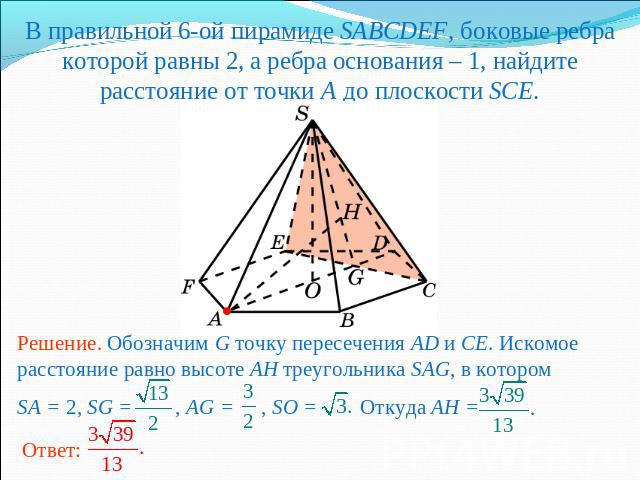
В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от точки A до плоскости SCE.Решение. Обозначим G точку пересечения AD и CE. Искомое расстояние равно высоте AH треугольника SAG, в которомSA = 2, SG = , AG = , SO = Откуда AH =