Презентация на тему: Расстояние от точки до плоскости

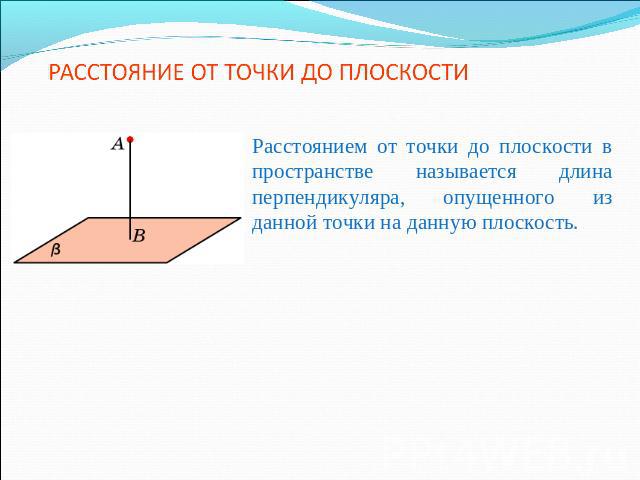
РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ Расстоянием от точки до плоскости в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость.

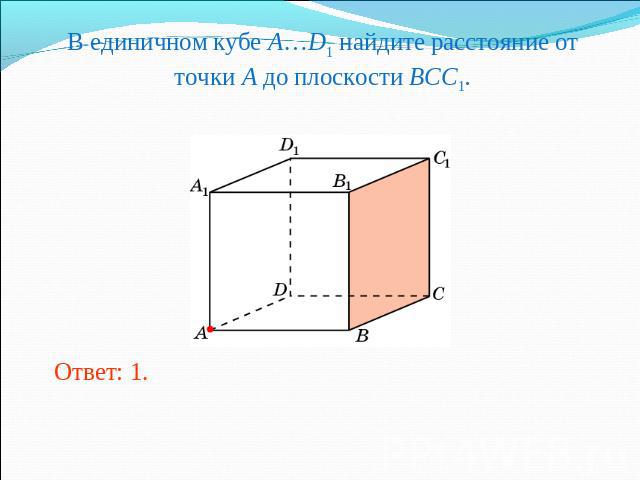
В единичном кубе A…D1 найдите расстояние от точки A до плоскости BCC1.

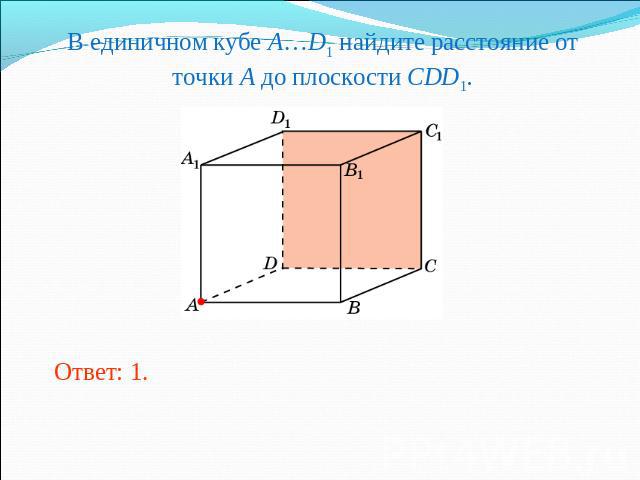
В единичном кубе A…D1 найдите расстояние от точки A до плоскости CDD1.
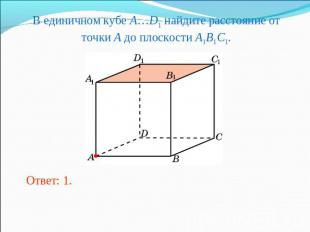
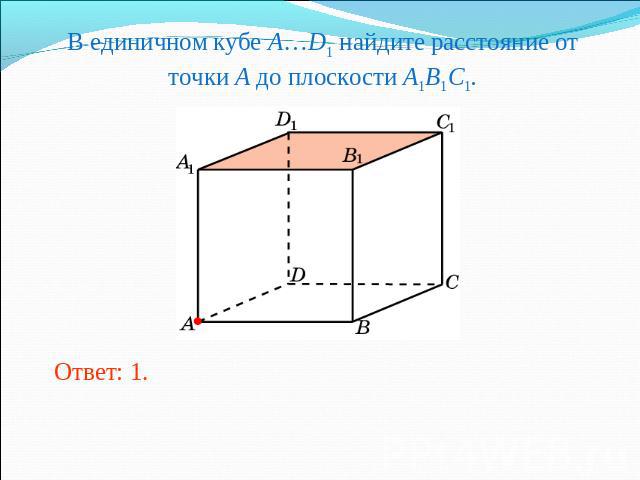
В единичном кубе A…D1 найдите расстояние от точки A до плоскости A1B1C1.
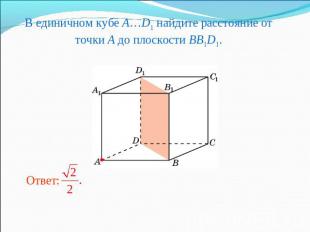
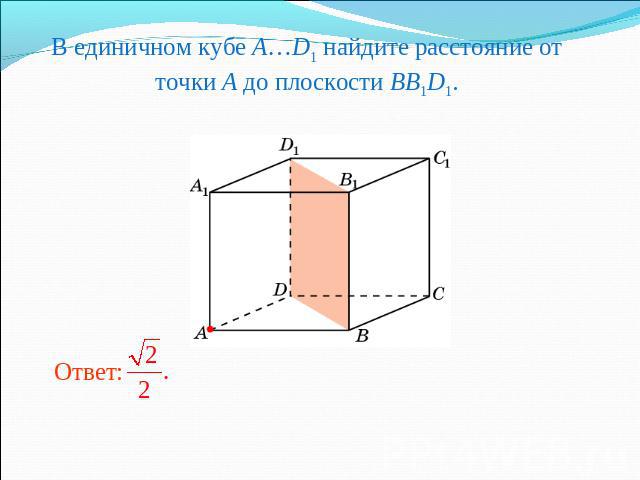
В единичном кубе A…D1 найдите расстояние от точки A до плоскости BB1D1.

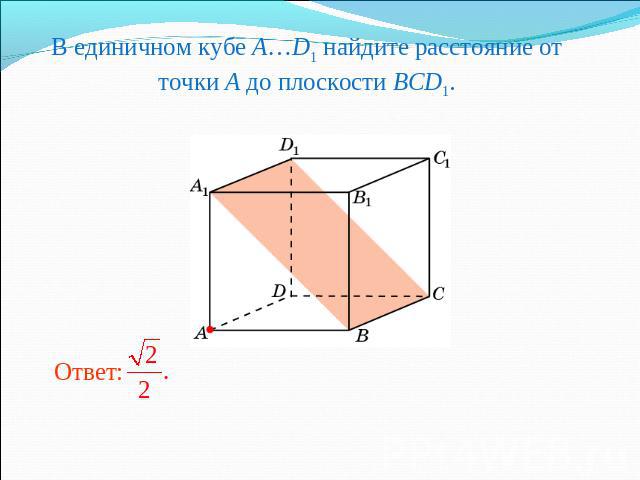
В единичном кубе A…D1 найдите расстояние от точки A до плоскости BCD1.

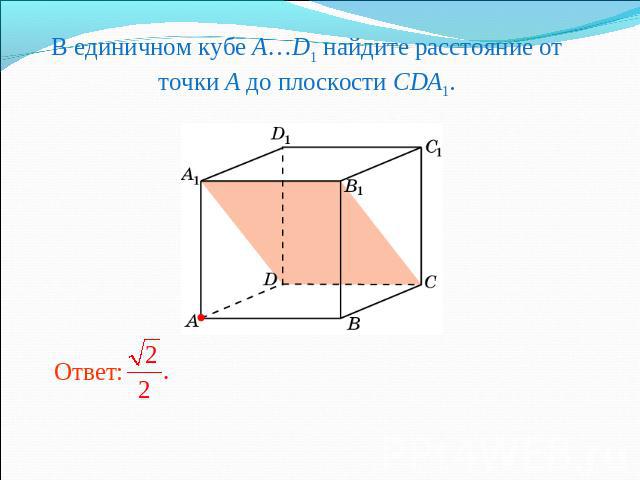
В единичном кубе A…D1 найдите расстояние от точки A до плоскости CDA1.

В единичном кубе A…D1 найдите расстояние от точки A до плоскости BDA1. Решение: Диагональ AC1 куба перпендикулярна плоскости BDA1. Обозначим O - центр грани ABCD, E - точка пересечения AC1 и плоскости BDA1. Длина отрезка AE будет искомым расстоянием. В прямоугольном треугольнике AOA1 имеемAA1 = 1; AO = ; OA1 = .Следовательно, AE =

В единичном кубе A…D1 найдите расстояние от точки A до плоскости CB1D1. Решение: Плоскость CB1D1 параллельна плоскости BDA1, и отстоит от вершины C1 на расстояние (см. предыдущую задачу). Учитывая, что длина диагонали куба равна , получим, что искомое расстояние AF равно .

В единичном кубе A…D1 найдите расстояние от точки A до плоскости BC1D. Решение: Обозначим O и O1 – центры граней куба. Прямая AO1 параллельна плоскости BC1D и, следовательно, расстояние от точки A до плоскости BC1D равно расстоянию от точки O1 до этой плоскости, т.е. высоте O1E треугольника OO1C1. ИмеемOO1 = 1; O1C = ; OC1 = .Следовательно, O1E =

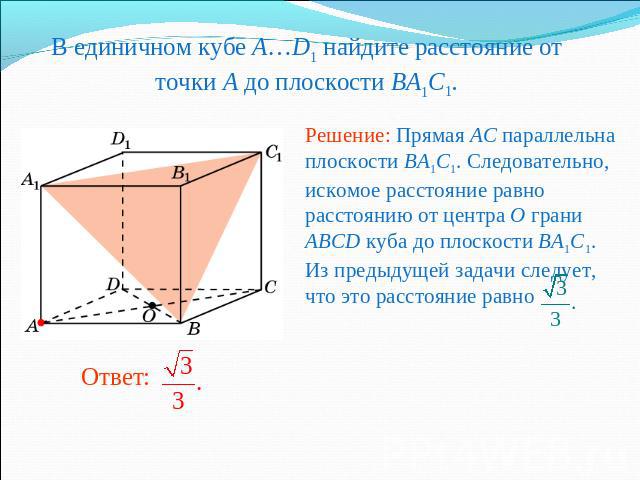
В единичном кубе A…D1 найдите расстояние от точки A до плоскости BA1C1.Решение: Прямая AC параллельна плоскости BA1C1. Следовательно, искомое расстояние равно расстоянию от центра O грани ABCD куба до плоскости BA1C1. Из предыдущей задачи следует, что это расстояние равно