Презентация на тему: Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)

Методы решениягеометрических задачЕГЭ, задание С2 (Расстояние от точки до плоскости)Подготовил: учитель математики МОУ «СОШ №10 с. Солдато-Александровского» Кобзев Д.А.
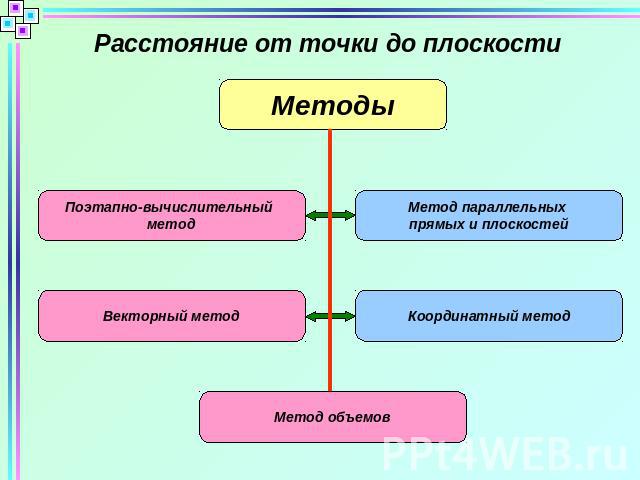
Расстояние от точки до плоскостиМетодыПоэтапно-вычислительный Метод параллельных Векторный методКоординатный методМетод объемов

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости А1В1С.

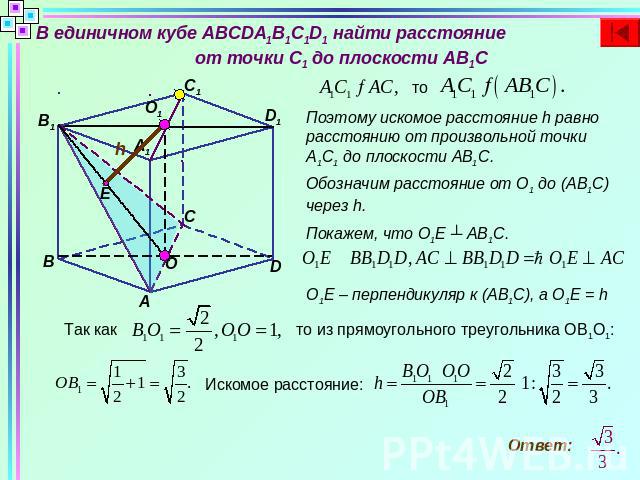
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки C1 до плоскости AB1CПоэтому искомое расстояние h равно расстоянию от произвольной точки А1С1 до плоскости АВ1С.Обозначим расстояние от О1 до (АВ1С) через h.

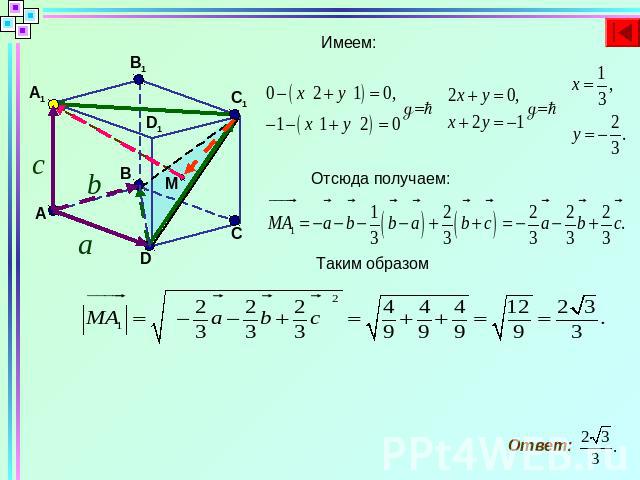
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1
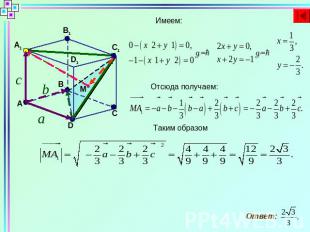
Имеем:
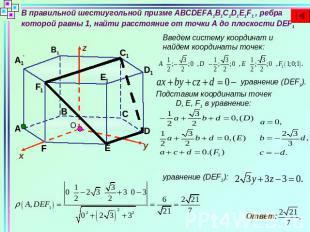
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости DEF1

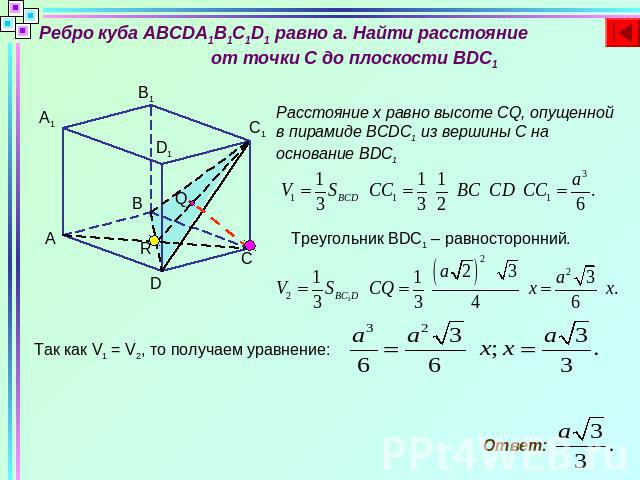
Ребро куба ABCDA1B1C1D1 равно а. Найти расстояние от точки C до плоскости BDC1Расстояние х равно высоте CQ, опущенной в пирамиде BCDC1 из вершины С на основание BDC1