Презентация на тему: Площадь

Геометрияглава 6 Площадь Подготовил Рокицкий Максим ученик 9 класса СПб лицей 488 (учитель Курышова Н.Е.)

Содержание Единица измеренияСвойства площадейПлощадь прямоугольникаПлощадь параллелограммаПлощадь треугольникаПлощадь трапецииТеорема ПифагораТеорема, обратная теореме Пифагора

Единица измерения Основная единица измерения – м2 (мм2, см2, км2, ар, га) 1 мм2 = 0,01 см21 см2 = 0,0001 м21 км2 = 1000000 м21 ар = 100 м21 гектар = 10000 м21 акр = 4046,8564224 м2 1 см x 1 см = 1 см2

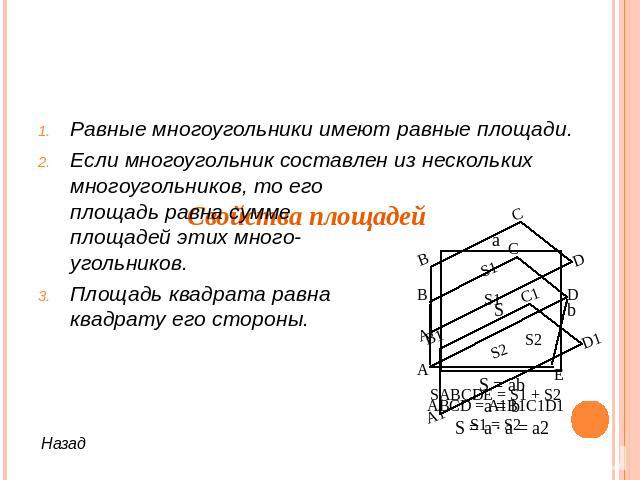
Равные многоугольники имеют равные площади.Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих много-угольников.Площадь квадрата равнаквадрату его стороны.

Дано: прямоугольник со сторонами a и b.Доказать: S = ab.Доказательство:(a + b)2 = S + S + a2 + b2а2 + 2ab +b2 = 2S + a2 + b2S = ab. Теорема доказана.

Задача: Найти площадь прямоугольника со сторонами 4 и 2.Дано: прямоугольник со сторонами a и b,a = 4 см, b = 2 см.Найти: S.Решение:S = abS = 4 см ∙ 2 см = 8 см2Ответ: S = 8 см2

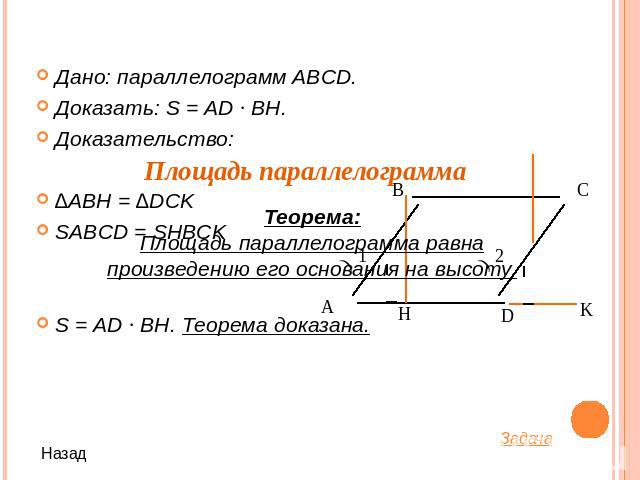
Дано: параллелограмм ABCD.Доказать: S = AD ∙ BH.Доказательство:∆ABH = ∆DCKSABCD = SHBCKS = AD ∙ BH. Теорема доказана.
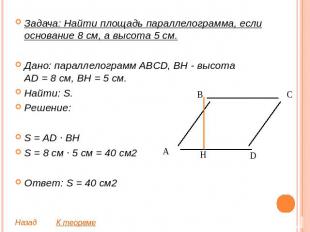
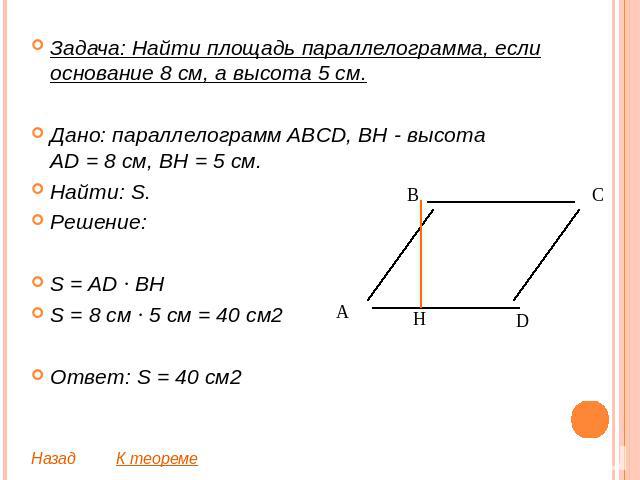
Задача: Найти площадь параллелограмма, если основание 8 см, а высота 5 см.Дано: параллелограмм ABCD, BH - высотаAD = 8 см, BH = 5 см.Найти: S.Решение:S = AD ∙ BHS = 8 см ∙ 5 см = 40 см2Ответ: S = 40 см2

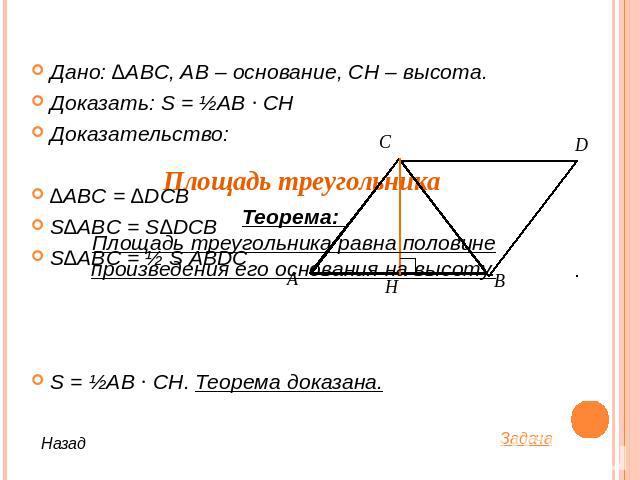
Дано: ∆ABC, AB – основание, CH – высота. Доказать: S = ½AB ∙ CHДоказательство:∆ABC = ∆DCBS∆ABC = S∆DCBS∆ABC = ½ S ABDCS = ½AB ∙ CH. Теорема доказана.
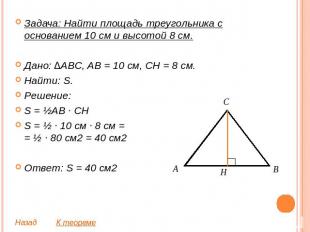
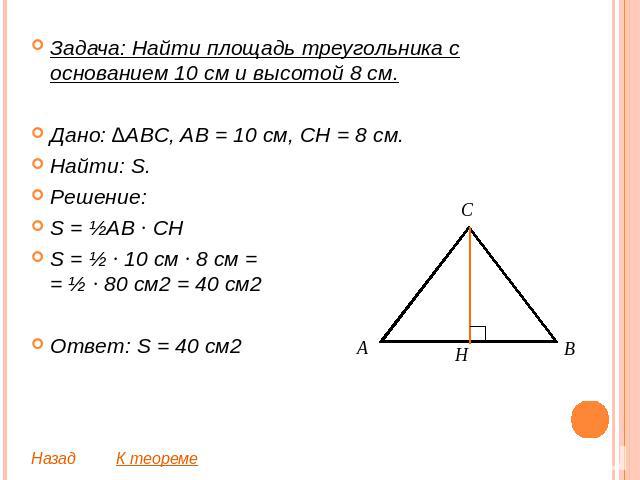
Задача: Найти площадь треугольника с основанием 10 см и высотой 8 см.Дано: ∆ABC, AB = 10 см, CH = 8 см. Найти: S.Решение:S = ½AB ∙ CHS = ½ ∙ 10 см ∙ 8 см == ½ ∙ 80 см2 = 40 см2Ответ: S = 40 см2

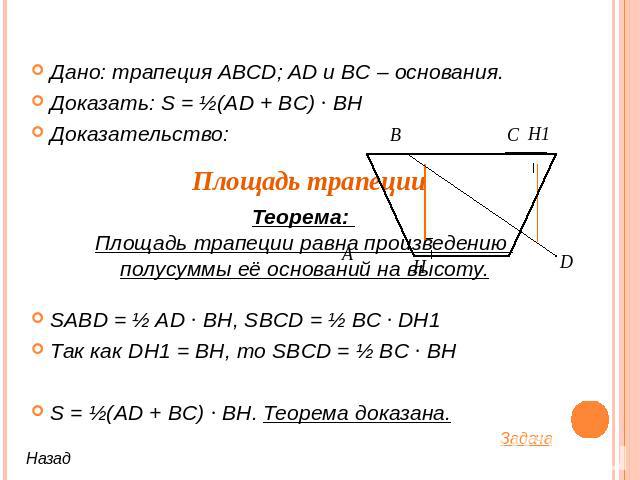
Дано: трапеция ABCD; AD и BC – основания.Доказать: S = ½(AD + BC) ∙ BHДоказательство:SABD = ½ AD ∙ BH, SBCD = ½ BC ∙ DH1 Так как DH1 = BH, то SBCD = ½ BC ∙ BHS = ½(AD + BC) ∙ BH. Теорема доказана. Теорема: Площадь трапеции равна произведению полусуммы её оснований на высоту.
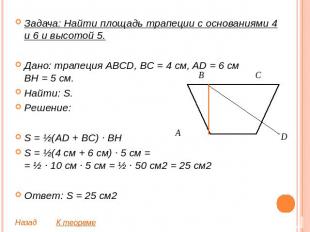
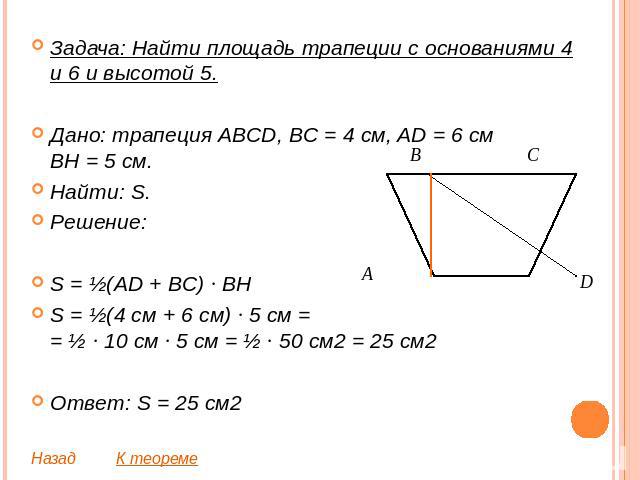
Задача: Найти площадь трапеции с основаниями 4 и 6 и высотой 5.Дано: трапеция ABCD, BC = 4 см, AD = 6 смBH = 5 см.Найти: S.Решение:S = ½(AD + BC) ∙ BHS = ½(4 см + 6 см) ∙ 5 см == ½ ∙ 10 см ∙ 5 см = ½ ∙ 50 см2 = 25 см2Ответ: S = 25 см2

Дано: a, b, c – стороны прямоугольного треугольникаДоказать: с2 = a2 + b2Доказательство:S = 4 ∙ ½ ab + c2 (a + b)2 = 2ab + c2с2 = a2 + b2. Теорема доказана.

Задача: Найти гипотенузу прямоугольного треугольника с катетами 4 и 3.Дано: ∆ABC, AC = 3 см, BC = 4 см, C – прямой.Найти: AB.Решение:AB2 = AC2 + BC2AB2 = 32 + 42 = 9 + 16 = 25AB = = 5 Ответ: AB = 5 см

Дано: ∆ABC; AB2 = AC2 + BC2Доказать: С – прямой уголДоказательство:A1C1 = AC, B1C1 = BCA1B12 = AC2 + BC2A1B12 = AB2, A1B1 = ABТеорема доказана.