Презентация на тему: Площадь 8 КЛАСС

Урок геометрии в 8 классе по теме «площадЬ» Сравнение математических фигур и величин служит материалом для игр и обучения мудростиПесталоцци И.Г. Учитель ГБОУ СОШ №380 Емелина Елена Георгиевна

Формулы площадей прямоугольного треугольника треугольника параллелограмма ромба, квадрата квадрата прямоугольника трапеции

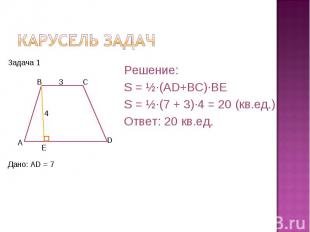
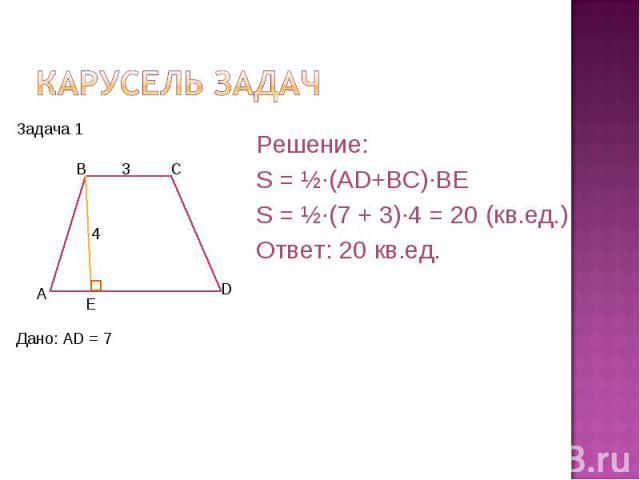
Карусель задач Решение:S = ½·(AD+BC)·BES = ½·(7 + 3)·4 = 20 (кв.ед.)Ответ: 20 кв.ед.

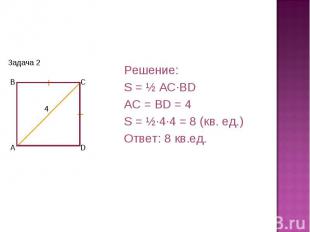
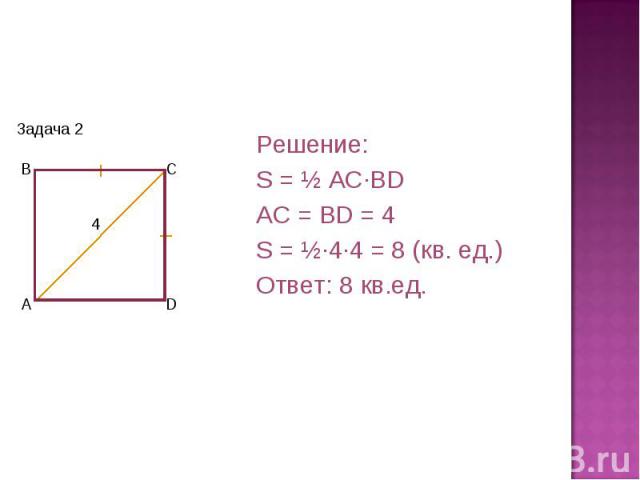
Решение:S = ½ AC·BDAC = BD = 4S = ½·4·4 = 8 (кв. ед.)Ответ: 8 кв.ед.

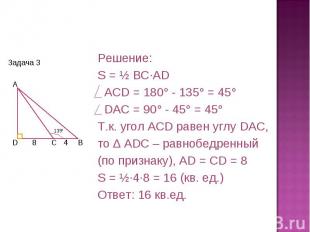
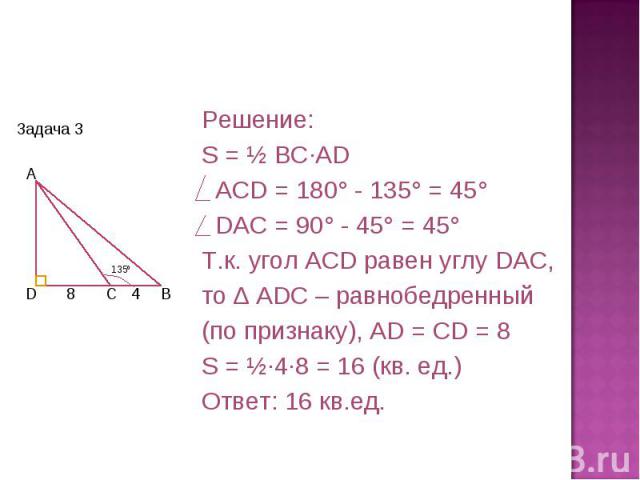
Решение:S = ½ BC·AD ACD = 180° - 135° = 45° DAC = 90° - 45° = 45° Т.к. угол ACD равен углу DAC,то ∆ ADC – равнобедренный(по признаку), AD = CD = 8 S = ½·4·8 = 16 (кв. ед.)Ответ: 16 кв.ед.

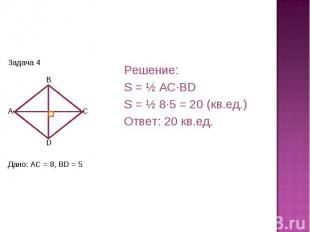
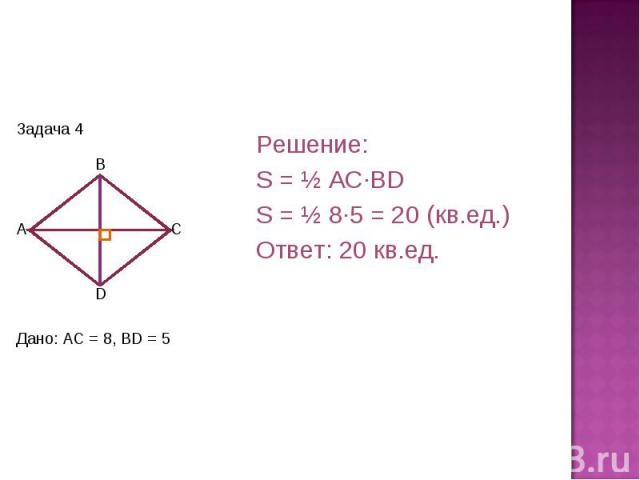
Решение:S = ½ AC·BDS = ½ 8·5 = 20 (кв.ед.)Ответ: 20 кв.ед. Дано: AC = 8, BD = 5

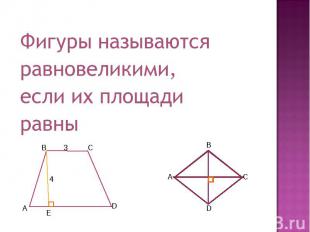
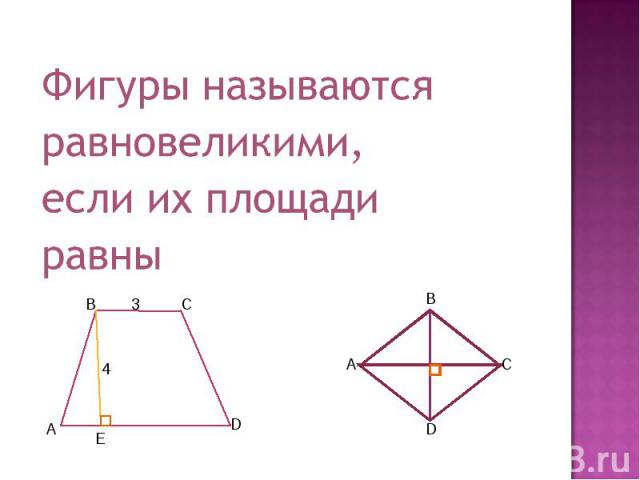
Фигуры называютсяравновеликими,если их площадиравны

Практическая работа. План. 1. Определить вид многоугольника 2. Выбрать соответствующую формулу 3. Сделать необходимые измерения 4. Вычислить площадь

Практическая работа Прямоугольный треугольникa = 5 смb = 13 смS = ½ abS = ½·5·13 = 32,5 (см2) Прямоугольная трапецияa = 5 смb = 8 смh = 8 см S = ½(a+b)hS = ½(5+8)·8 = 52 (см2) Сумма площадей 4-х фигур:S общ = 32,5 + 32,5 + 52 + 52 = 169 (см2)

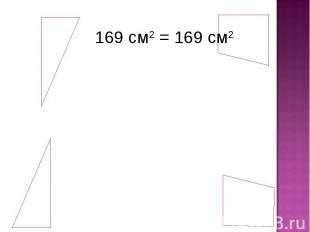
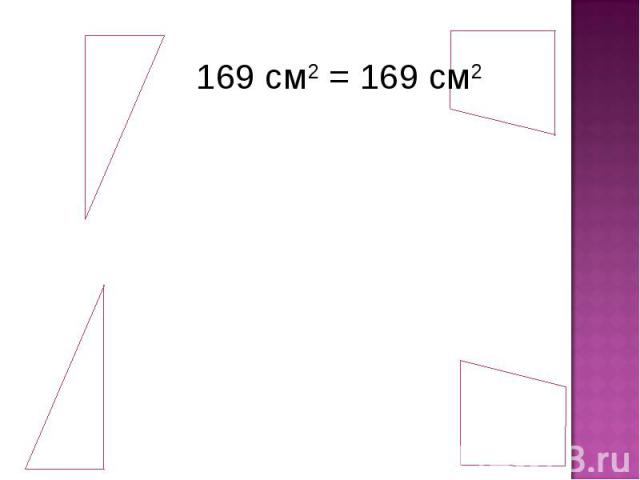
169 см2 = 169 см2

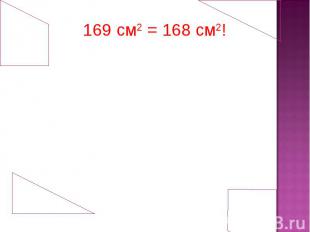
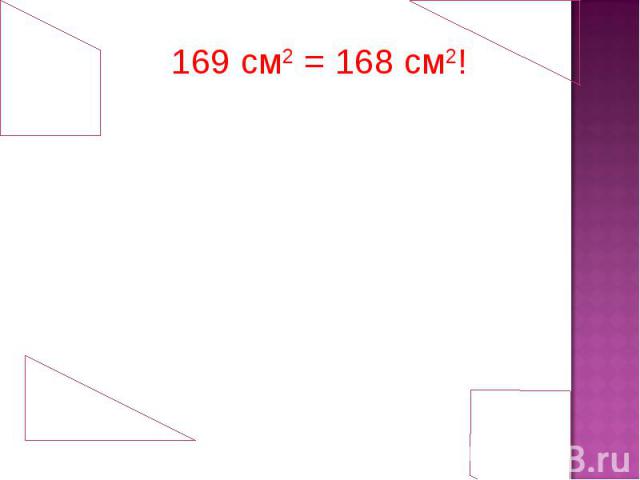
169 см2 = 168 см2!

СОфизм Софизм (от греч. σόφισμα, «мастерство, умение, хитрая выдумка, уловка») — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным.

ДОМАШHЕЕ ЗАДАНИЕ По планированию учителя.

Спасибо за внимание и сотрудничество!