Презентация на тему: Пирамида, вписанная в конус

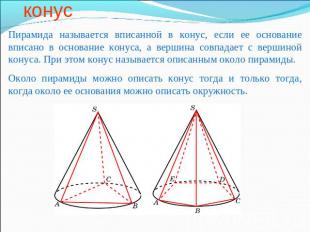
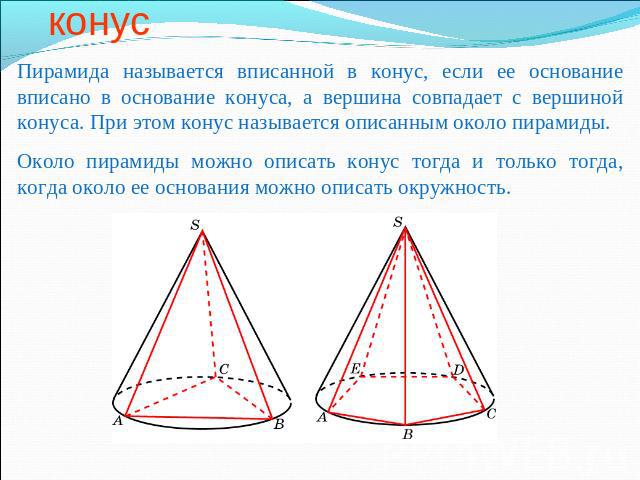
Пирамида, вписанная в конус Пирамида называется вписанной в конус, если ее основание вписано в основание конуса, а вершина совпадает с вершиной конуса. При этом конус называется описанным около пирамиды.Около пирамиды можно описать конус тогда и только тогда, когда около ее основания можно описать окружность.

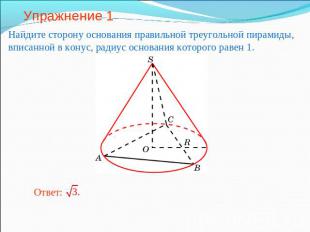
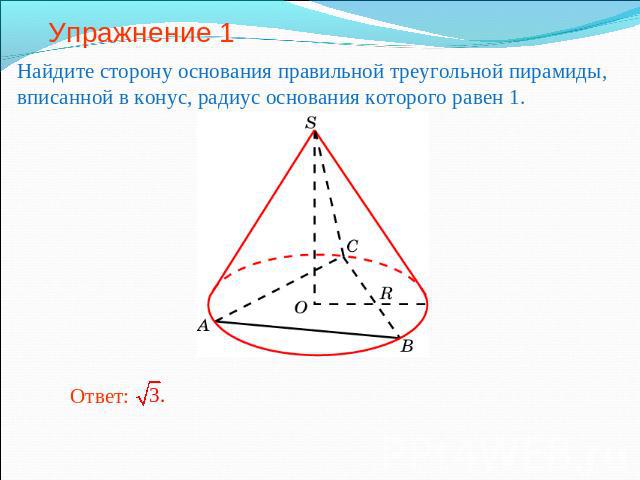
Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

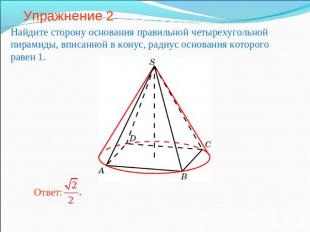
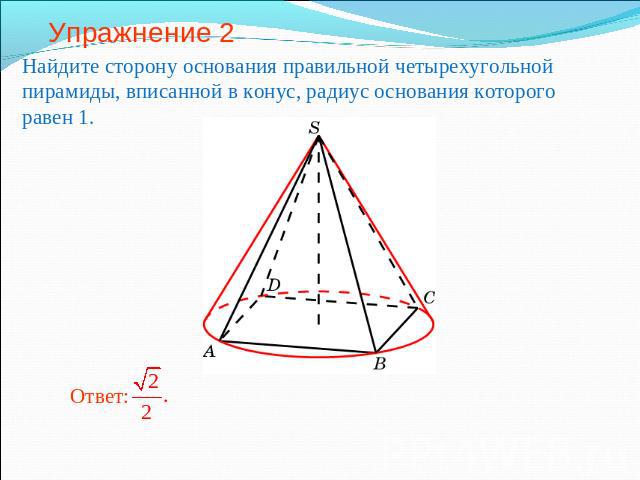
Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

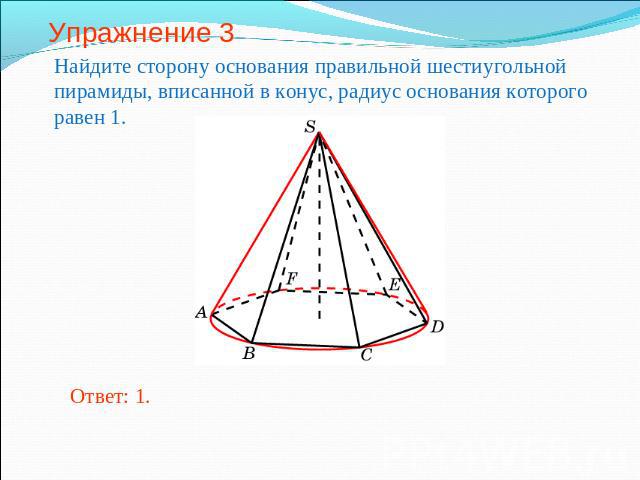
Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, вписанной в конус, радиус основания которого равен 1.

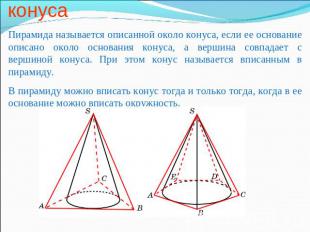
Пирамида, описанная около конуса Пирамида называется описанной около конуса, если ее основание описано около основания конуса, а вершина совпадает с вершиной конуса. При этом конус называется вписанным в пирамиду. В пирамиду можно вписать конус тогда и только тогда, когда в ее основание можно вписать окружность.

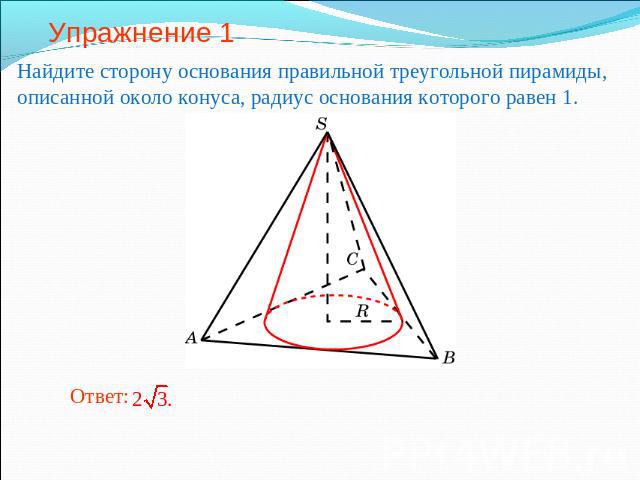
Упражнение 1 Найдите сторону основания правильной треугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

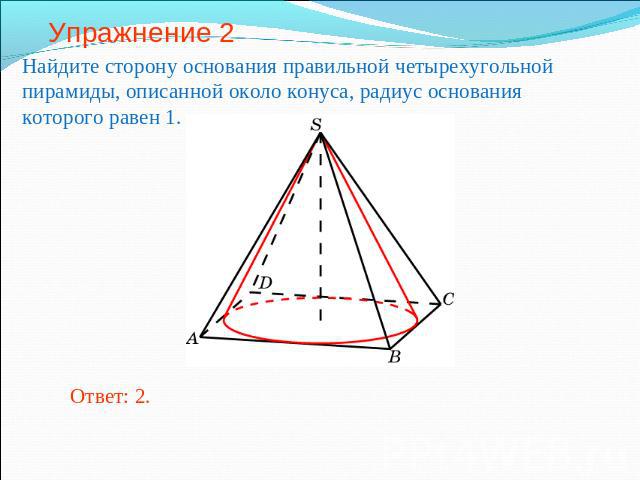
Упражнение 2 Найдите сторону основания правильной четырехугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

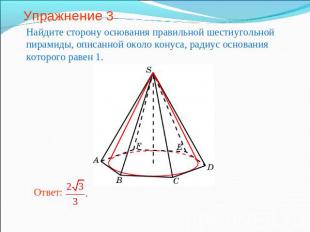
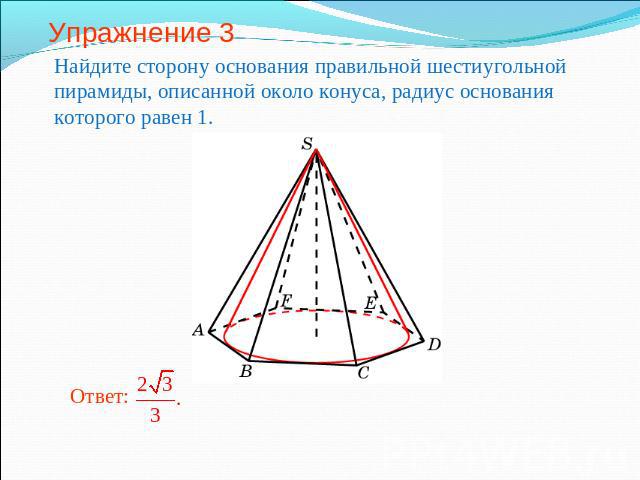
Упражнение 3 Найдите сторону основания правильной шестиугольной пирамиды, описанной около конуса, радиус основания которого равен 1.

Сфера, вписанная в конус Сфера называется вписанной в конус, если она касается его основания и боковой поверхности (касается каждой образующей). При этом конус называется описанным около сферы.В любой конус (прямой, круговой) можно вписать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.Напомним, что радиус r окружности, вписанный в треугольник, находится по формулегде S – площадь, p – полупериметр треугольника.

Упражнение 1 В конус, радиус основания которого равен 1, а образующая равна 2, вписана сфера. Найдите ее радиус.Решение. Треугольник SAB равносторонний. Высота SH равна Площадь S равна Полупериметр p равен 3. По формуле r = S/p получаем

Упражнение 2 В конус, радиус основания которого равен 2, вписана сфера радиуса 1. Найдите высоту конуса.Решение. Обозначим h высоту SH конуса. Из формулы r = S/p имеем: где r = 1, a = FG = 4, p =Решая уравнение находим

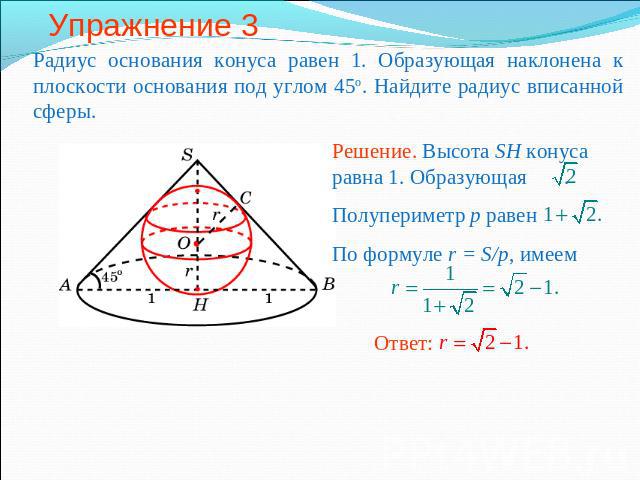
Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус вписанной сферы.Решение. Высота SH конуса равна 1. Образующая .Полупериметр p равенПо формуле r = S/p, имеем

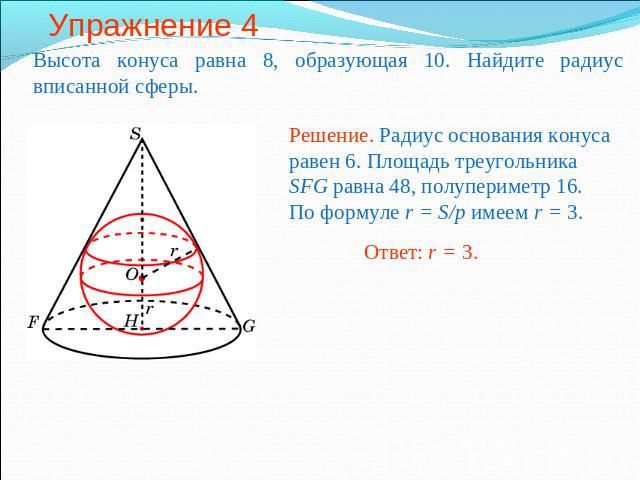
Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус вписанной сферы.Решение. Радиус основания конуса равен 6. Площадь треугольника SFG равна 48, полупериметр 16. По формуле r = S/p имеем r = 3.

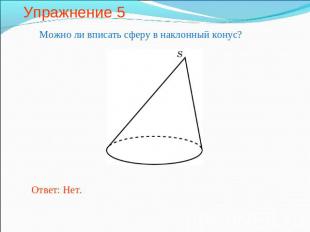
Упражнение 5 Можно ли вписать сферу в наклонный конус?

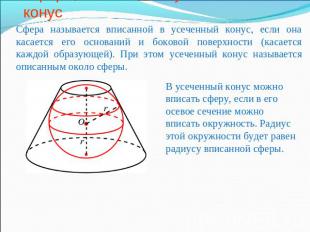
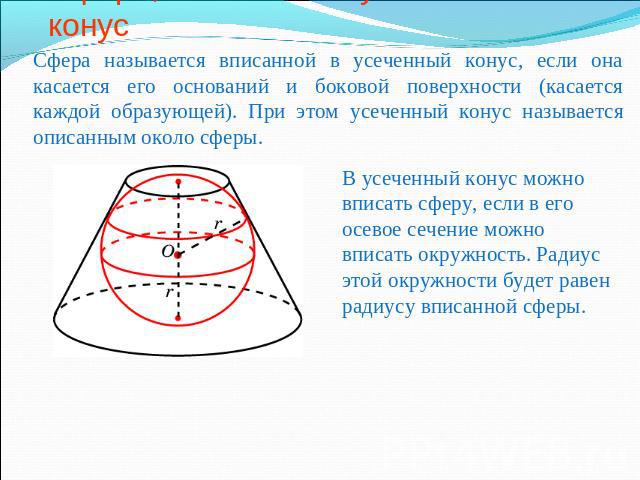
Сфера, вписанная в усеченный конус Сфера называется вписанной в усеченный конус, если она касается его оснований и боковой поверхности (касается каждой образующей). При этом усеченный конус называется описанным около сферы.В усеченный конус можно вписать сферу, если в его осевое сечение можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.

Упражнение 1В усеченный конус, радиусы оснований которого равны 2 и 1, вписана сфера. Найдите радиус сферы и высоту усеченного конуса.Решение. Имеем: A1B = A1O1= 2, A2B = A2O2= 1. Следовательно, A1A2 = 3, A1C = 1.

Упражнение 2 В усеченный конус, радиус одного основания которого равен 2, вписана сфера радиуса 1. Найдите радиус второго основания.Решение. Пусть A1O1= 2. Обозначим r = A2O2. Имеем: A1A2 = 2+r, A1C = 2 – r. По теореме Пифагора, имеет место равенство из которого следует, что выполняется равенство Решая полученное уравнение относительно r, находим

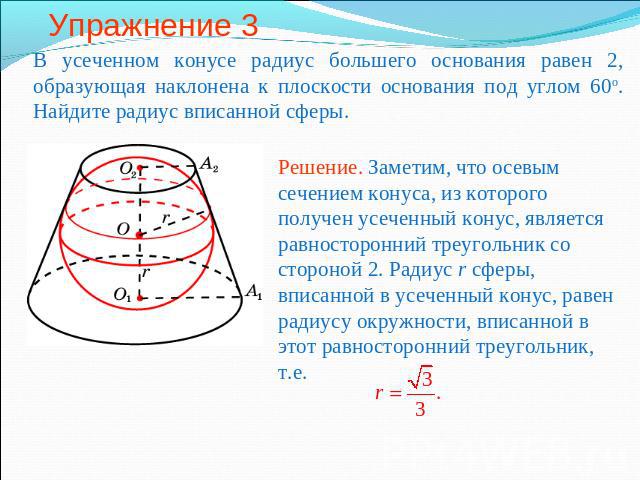
Упражнение 3 В усеченном конусе радиус большего основания равен 2, образующая наклонена к плоскости основания под углом 60о. Найдите радиус вписанной сферы.Решение. Заметим, что осевым сечением конуса, из которого получен усеченный конус, является равносторонний треугольник со стороной 2. Радиус r сферы, вписанной в усеченный конус, равен радиусу окружности, вписанной в этот равносторонний треугольник, т.е.

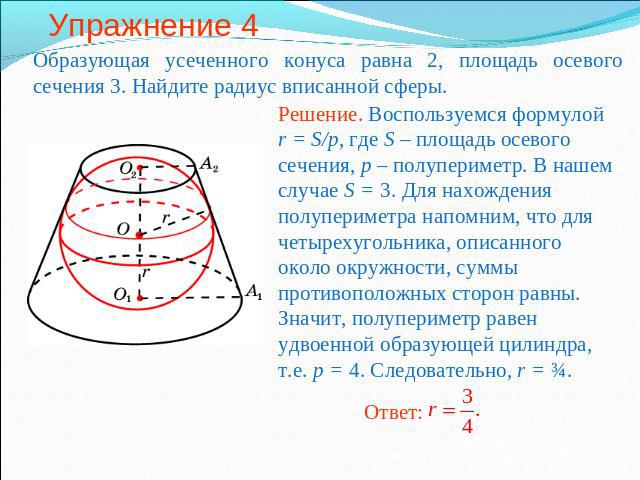
Упражнение 4 Образующая усеченного конуса равна 2, площадь осевого сечения 3. Найдите радиус вписанной сферы.Решение. Воспользуемся формулой r = S/p, где S – площадь осевого сечения, p – полупериметр. В нашем случае S = 3. Для нахождения полупериметра напомним, что для четырехугольника, описанного около окружности, суммы противоположных сторон равны. Значит, полупериметр равен удвоенной образующей цилиндра, т.е. p = 4. Следовательно, r = ¾.

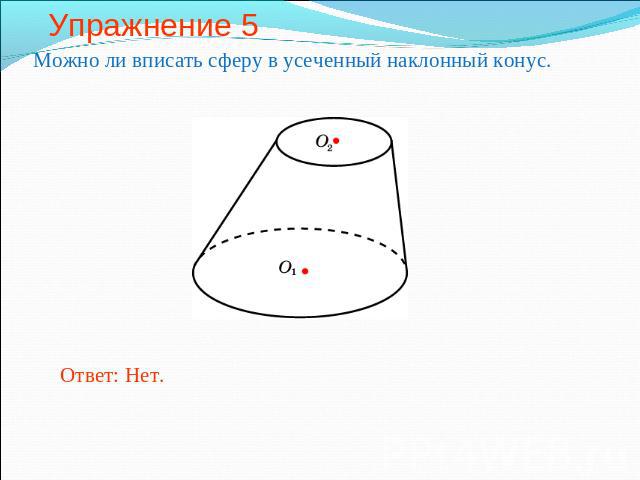
Упражнение 5 Можно ли вписать сферу в усеченный наклонный конус.

Сфера, описанная около конуса Сфера называется описанной около конуса, если вершина и окружность основания конуса лежат на сфере. При этом конус называется вписанным в сферу. Около любого конуса (прямого, кругового) можно описать сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.Напомним, что радиус R окружности, описанной около треугольника, находится по формулегде S – площадь, a, b, c – стороны треугольника.

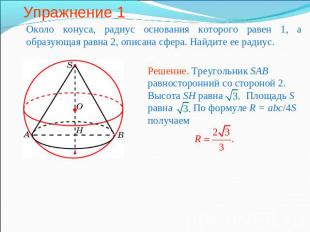
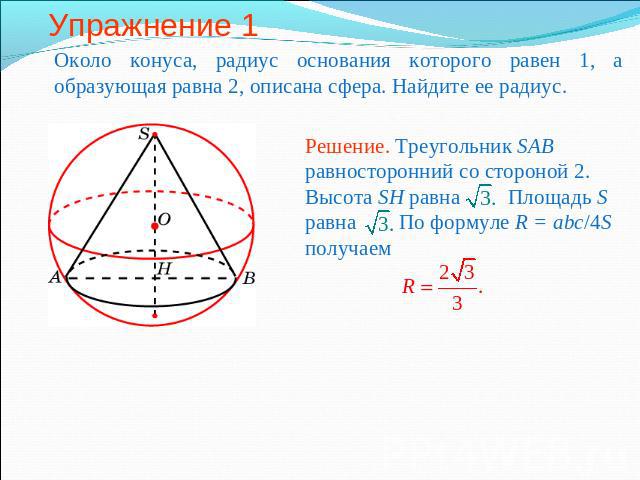
Упражнение 1 Около конуса, радиус основания которого равен 1, а образующая равна 2, описана сфера. Найдите ее радиус.Решение. Треугольник SAB равносторонний со стороной 2. Высота SH равна Площадь S равна По формуле R = abc/4S получаем

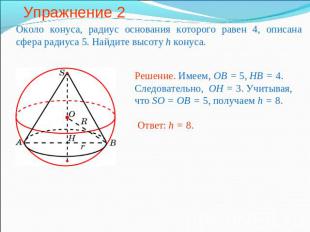
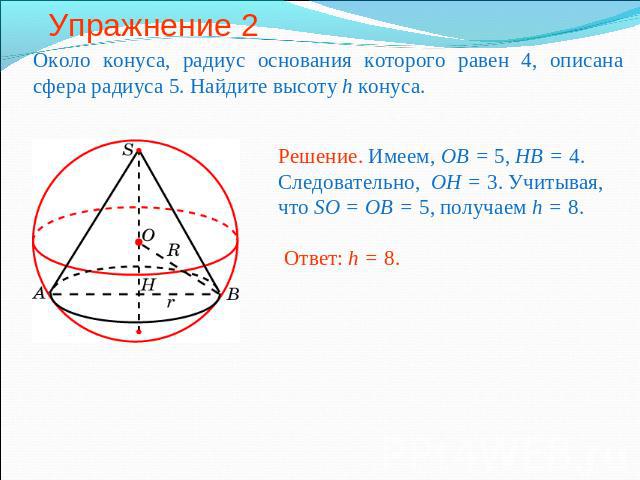
Упражнение 2 Около конуса, радиус основания которого равен 4, описана сфера радиуса 5. Найдите высоту h конуса.Решение. Имеем, OB = 5, HB = 4. Следовательно, OH = 3. Учитывая, что SO = OB = 5, получаем h = 8.

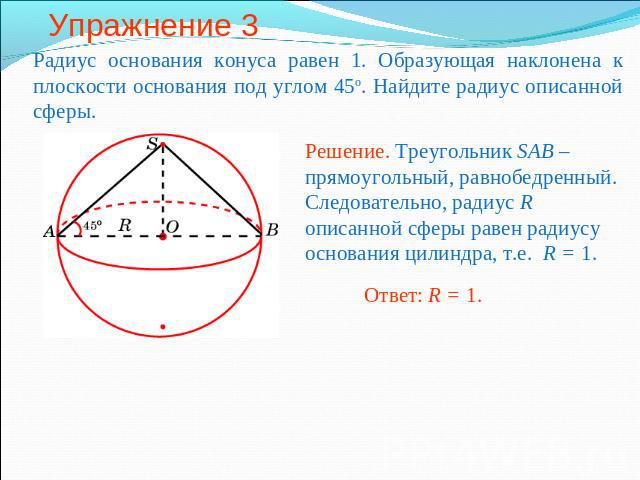
Упражнение 3 Радиус основания конуса равен 1. Образующая наклонена к плоскости основания под углом 45о. Найдите радиус описанной сферы.Решение. Треугольник SAB – прямоугольный, равнобедренный. Следовательно, радиус R описанной сферы равен радиусу основания цилиндра, т.е. R = 1.

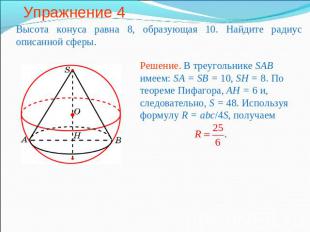
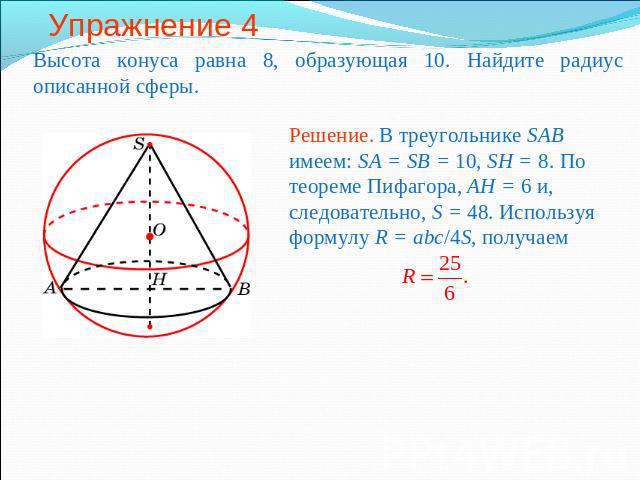
Упражнение 4 Высота конуса равна 8, образующая 10. Найдите радиус описанной сферы.Решение. В треугольнике SAB имеем: SA = SB = 10, SH = 8. По теореме Пифагора, AH = 6 и, следовательно, S = 48. Используя формулу R = abc/4S, получаем

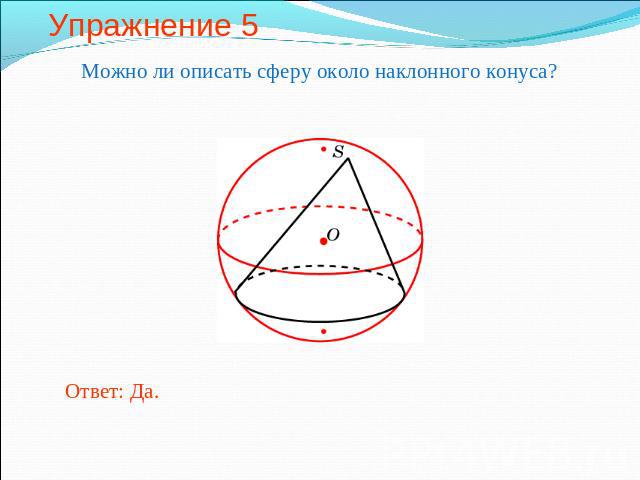
Упражнение 5 Можно ли описать сферу около наклонного конуса?

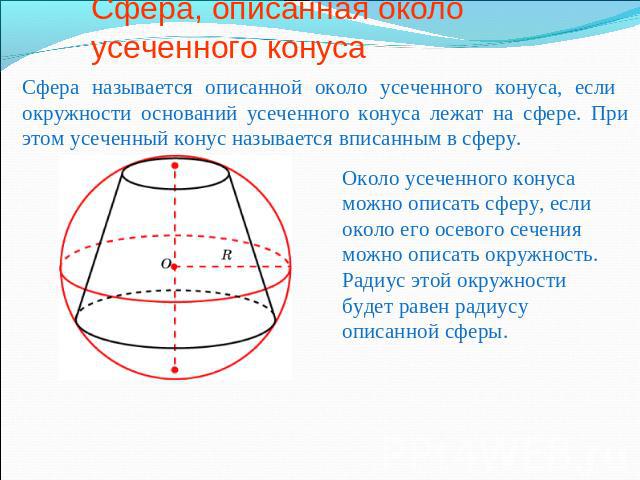
Сфера, описанная около усеченного конуса Сфера называется описанной около усеченного конуса, если окружности оснований усеченного конуса лежат на сфере. При этом усеченный конус называется вписанным в сферу.Около усеченного конуса можно описать сферу, если около его осевого сечения можно описать окружность. Радиус этой окружности будет равен радиусу описанной сферы.

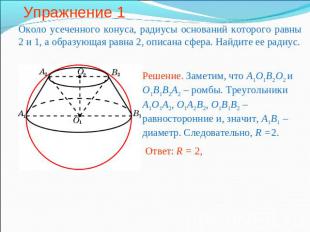
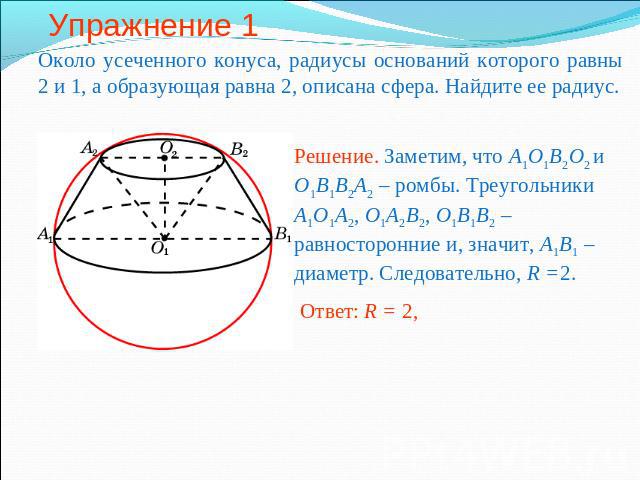
Упражнение 1 Около усеченного конуса, радиусы оснований которого равны 2 и 1, а образующая равна 2, описана сфера. Найдите ее радиус.Решение. Заметим, что A1O1B2O2 и O1B1B2A2 – ромбы. Треугольники A1O1A2, O1A2B2, O1B1B2 – равносторонние и, значит, A1B1 –диаметр. Следовательно, R =2.

Упражнение 2 Радиус меньшего основания усеченного конуса равен 1, образующая равна 2 и составляет угол 45о с плоскостью другого основания. Найдите радиус описанной сферы.Решение. Имеем A2O2 = 1, A1A2 = 2, O1O2 = , OO1 = O1C = 1. Следовательно, OO2 = 1 + и, значит,

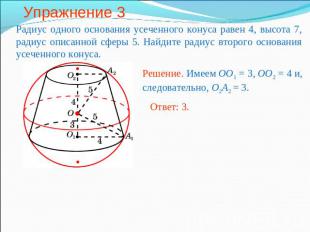
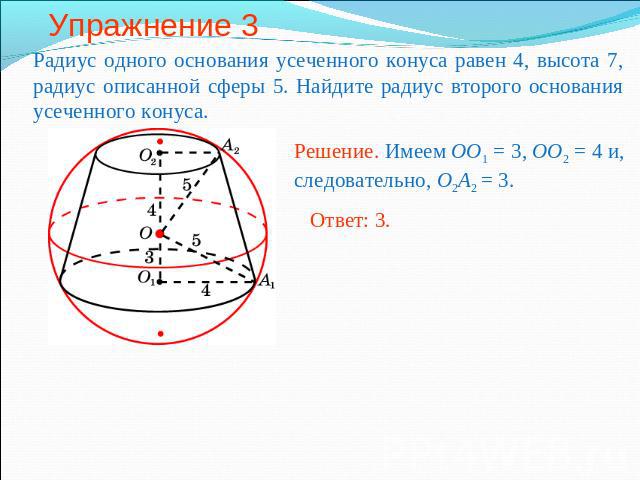
Упражнение 3 Радиус одного основания усеченного конуса равен 4, высота 7, радиус описанной сферы 5. Найдите радиус второго основания усеченного конуса. Решение. Имеем OO1 = 3, OO2 = 4 и, следовательно, O2A2 = 3.

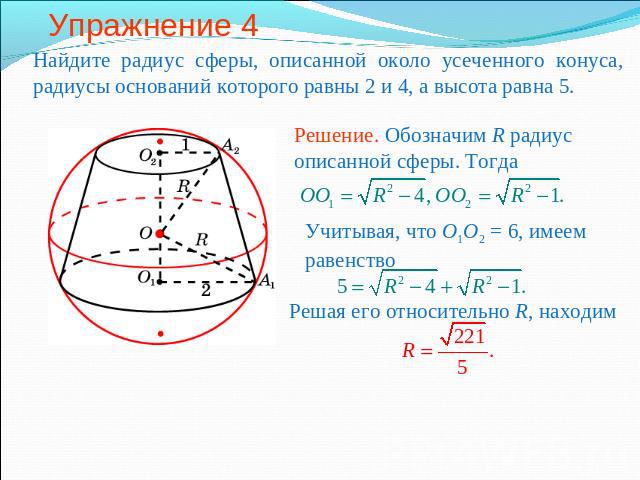
Упражнение 4 Найдите радиус сферы, описанной около усеченного конуса, радиусы оснований которого равны 2 и 4, а высота равна 5. Решение. Обозначим R радиус описанной сферы. Тогда

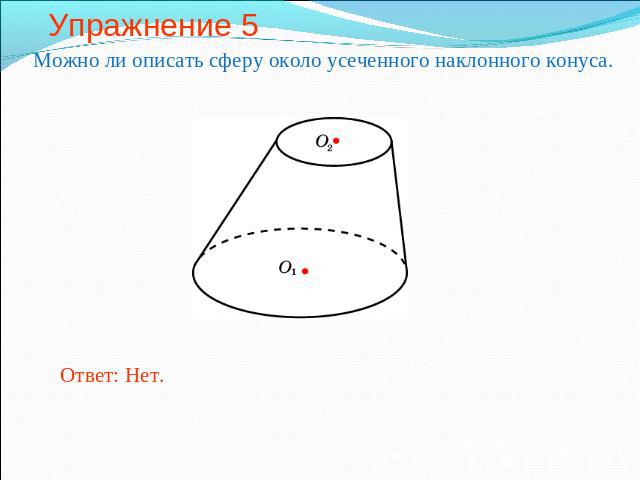
Упражнение 5 Можно ли описать сферу около усеченного наклонного конуса.