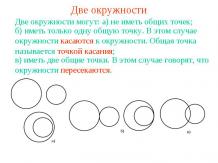
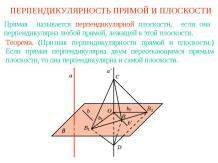
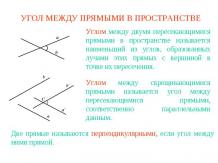
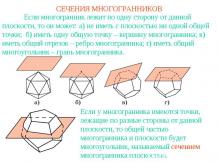
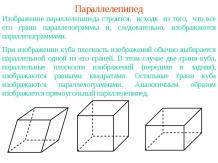
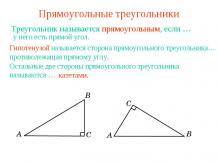
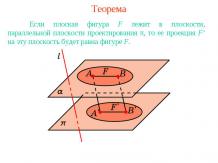
Презентация на тему: Задачи на построение

Задачи на построениеОсновными чертежными инструментами, с помощью которых производятся геометрические построения, являются линейка и циркуль.С помощью линейки через две заданные точки проводят прямую. С помощью циркуля проводят окружности с данным центром и данного радиуса. В частности, с помощью циркуля на луче от его начала можно отложить отрезок, равный данному.

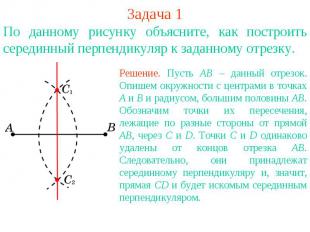
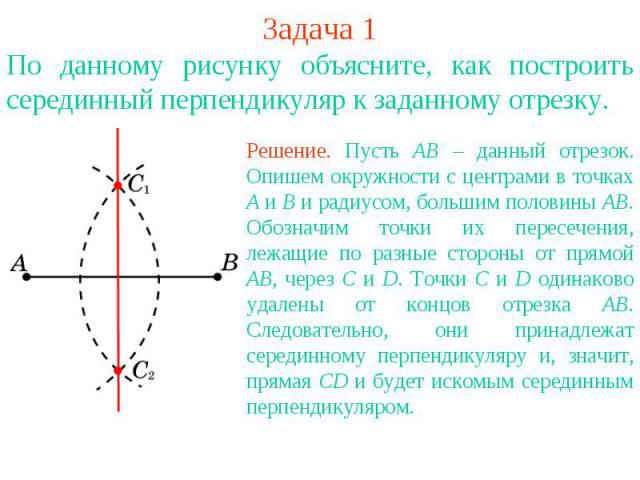
Задача 1По данному рисунку объясните, как построить серединный перпендикуляр к заданному отрезку. Решение. Пусть АВ – данный отрезок. Опишем окружности с центрами в точках А и В и радиусом, большим половины АВ. Обозначим точки их пересечения, лежащие по разные стороны от прямой АВ, через С и D. Точки С и D одинаково удалены от концов отрезка АВ. Следовательно, они принадлежат серединному перпендикуляру и, значит, прямая CD и будет искомым серединным перпендикуляром.

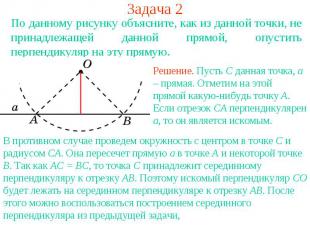
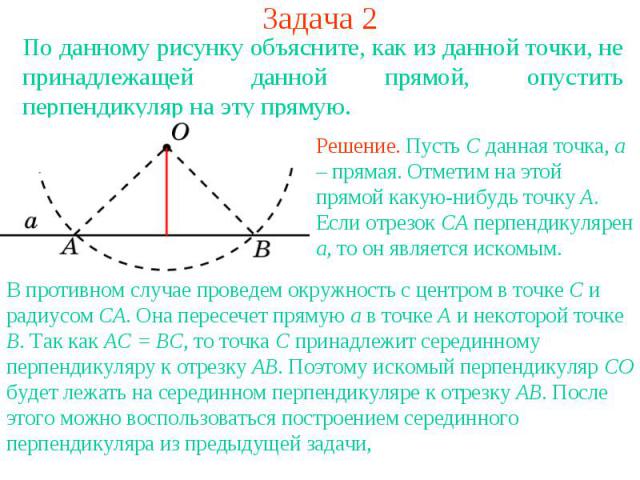
Задача 2По данному рисунку объясните, как из данной точки, не принадлежащей данной прямой, опустить перпендикуляр на эту прямую.Решение. Пусть C данная точка, a – прямая. Отметим на этой прямой какую-нибудь точку A. Если отрезок CA перпендикулярен a, то он является искомым.В противном случае проведем окружность с центром в точке C и радиусом CA. Она пересечет прямую a в точке A и некоторой точке B. Так как AC = BC, то точка C принадлежит серединному перпендикуляру к отрезку AB. Поэтому искомый перпендикуляр CO будет лежать на серединном перпендикуляре к отрезку AB. После этого можно воспользоваться построением серединного перпендикуляра из предыдущей задачи,

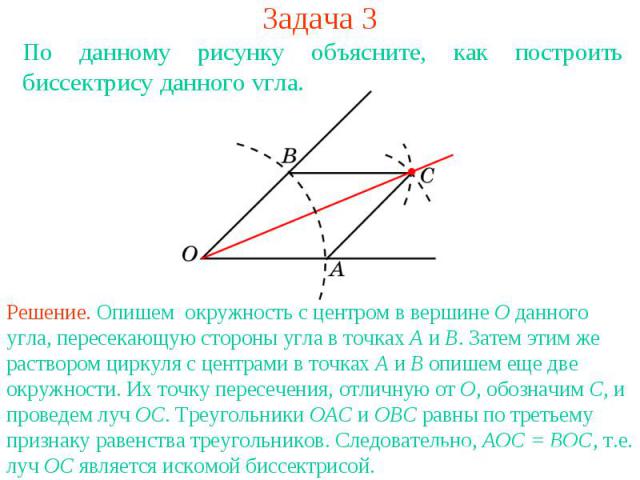
Задача 3По данному рисунку объясните, как построить биссектрису данного угла.Решение. Опишем окружность с центром в вершине О данного угла, пересекающую стороны угла в точках А и В. Затем этим же раствором циркуля с центрами в точках А и В опишем еще две окружности. Их точку пересечения, отличную от О, обозначим С, и проведем луч ОС. Треугольники ОАС и ОВС равны по третьему признаку равенства треугольников. Следовательно, AOC = BOC, т.е. луч ОС является искомой биссектрисой.

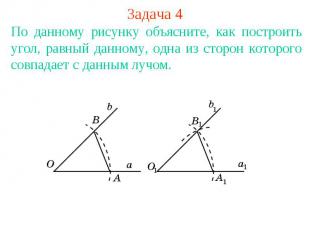
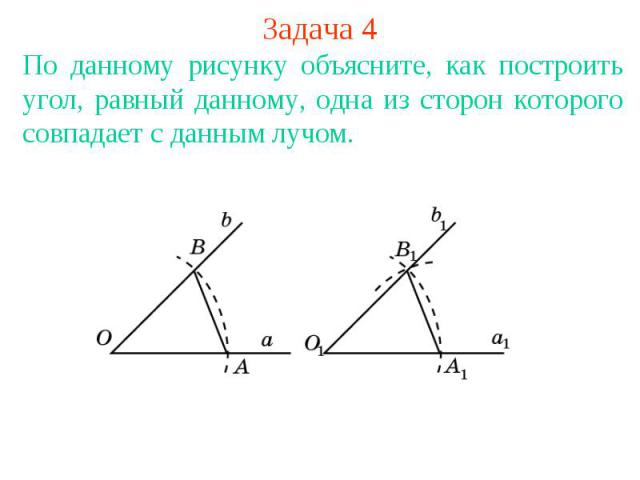
Задача 4По данному рисунку объясните, как построить угол, равный данному, одна из сторон которого совпадает с данным лучом.

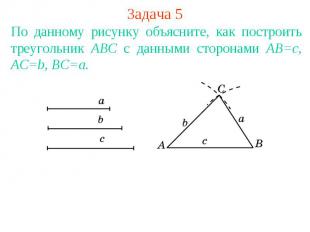
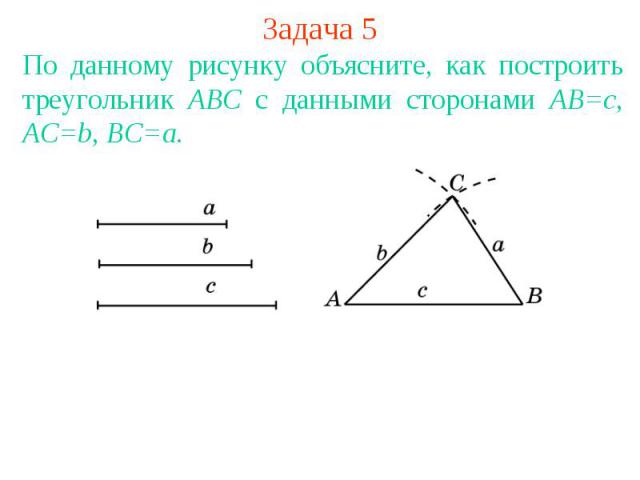
Задача 5По данному рисунку объясните, как построить треугольник АВС с данными сторонами АВ=с, АС=b, ВС=a.

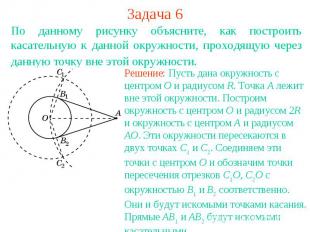
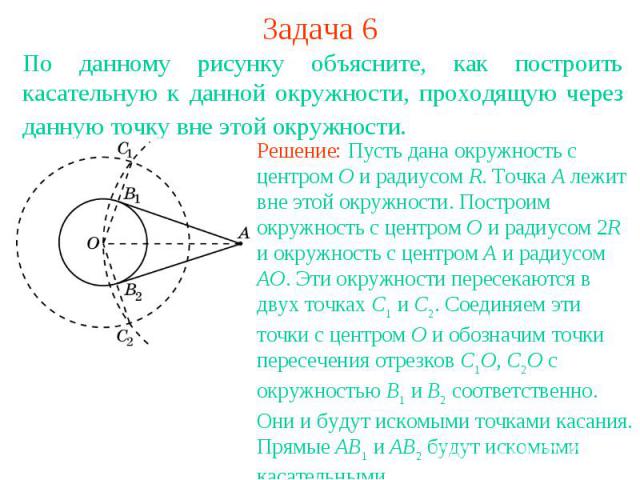
Задача 6По данному рисунку объясните, как построить касательную к данной окружности, проходящую через данную точку вне этой окружности. Решение: Пусть дана окружность с центром O и радиусом R. Точка A лежит вне этой окружности. Построим окружность с центром O и радиусом 2R и окружность с центром A и радиусом AO. Эти окружности пересекаются в двух точках C1 и C2. Соединяем эти точки с центром O и обозначим точки пересечения отрезков C1O, C2O с окружностью B1 и B2 соответственно. Они и будут искомыми точками касания. Прямые AB1 и AB2 будут искомыми касательными.

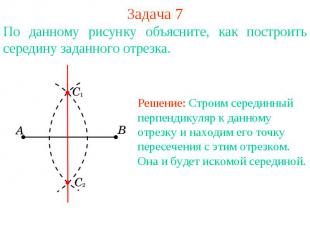
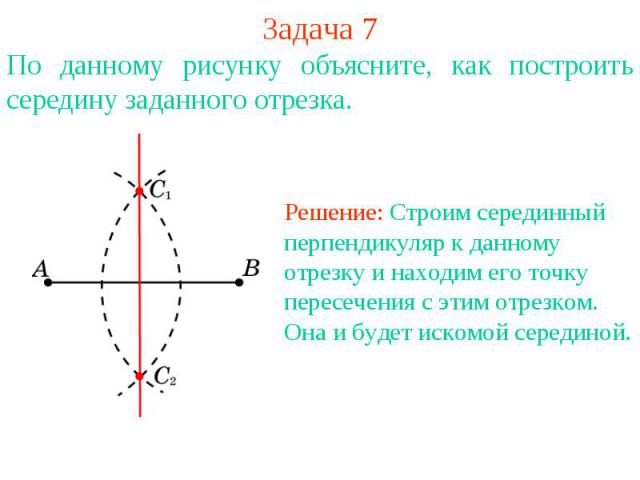
Задача 7По данному рисунку объясните, как построить середину заданного отрезка. Решение: Строим серединный перпендикуляр к данному отрезку и находим его точку пересечения с этим отрезком. Она и будет искомой серединой.