Презентация на тему: Угол между прямой и плоскостью

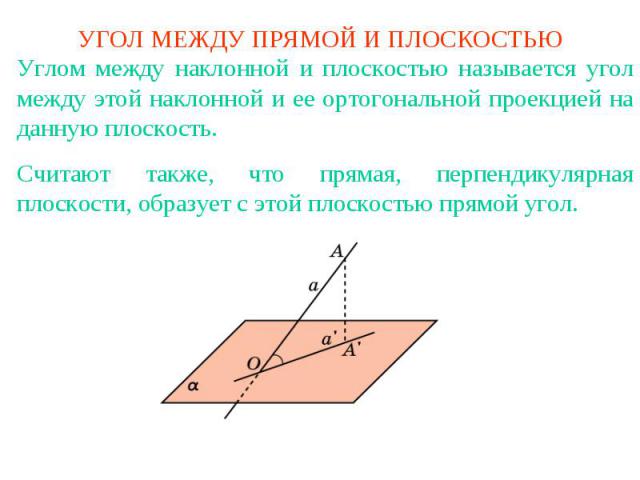
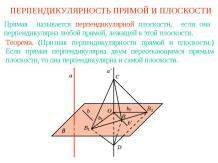
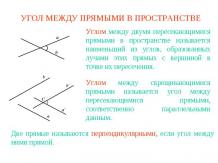
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮУглом между наклонной и плоскостью называется угол между этой наклонной и ее ортогональной проекцией на данную плоскость.Считают также, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.
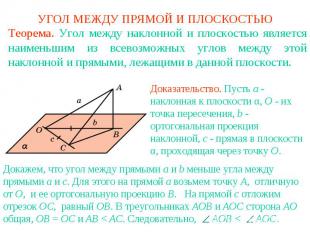
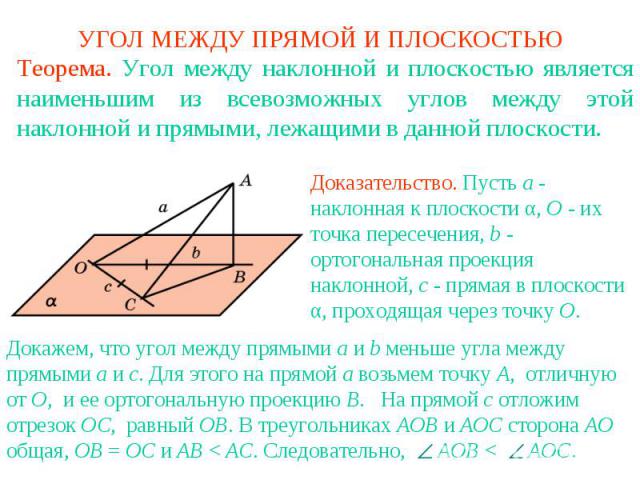
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮТеорема. Угол между наклонной и плоскостью является наименьшим из всевозможных углов между этой наклонной и прямыми, лежащими в данной плоскости.Доказательство. Пусть a - наклонная к плоскости α, О - их точка пересечения, b - ортогональная проекция наклонной, c - прямая в плоскости α, проходящая через точку О. Докажем, что угол между прямыми a и b меньше угла между прямыми a и c. Для этого на прямой a возьмем точку А, отличную от О, и ее ортогональную проекцию B. На прямой c отложим отрезок ОC, равный ОB. В треугольниках АОB и AOC сторона АО общая, ОB = OC и AB < AC. Следовательно, AOB < AOC.

Упражнение 1Прямые a и b образуют с плоскостью α равные углы. Будут ли эти прямые параллельны?

Упражнение 2Две плоскости образуют с данной прямой равные углы. Как расположены плоскости относительно друг друга?Ответ: Параллельны или пересекаются.

Упражнение 3Под каким углом к плоскости нужно провести отрезок, чтобы его ортогональная проекция на эту плоскость была вдвое меньше самого отрезка?

Упражнение 4Может ли катет равнобедренного прямоугольного треугольника образовать с плоскостью, проходящей через гипотенузу, угол в 60°? Каков наибольший угол между катетом и этой плоскостью?

Упражнение 5Одна из двух скрещивающихся прямых пересекает плоскость под углом 60°, а другая перпендикулярна этой плоскости. Найдите угол между данными скрещивающимися прямыми.

Упражнение 6В кубе найдите угол между: а) диагональю боковой грани и плоскостью основания; б) диагональю куба и плоскостью основания; в) диагональю боковой грани и диагональным сечением.

Упражнение 7Найдите угол между ребром правильного тетраэдра и не содержащей его гранью.

Упражнение 8В правильной треугольной пирамиде сторона основания равна а, а боковое ребро b. Найдите угол наклона бокового ребра к плоскости основания.

Упражнение 9Будут ли в пирамиде боковые ребра равны, если они образуют равные углы с плоскостью основания?

Упражнение 10Через сторону квадрата проведена плоскость, составляющая с диагональю квадрата угол 30°. Найдите углы, которые образуют с плоскостью стороны квадрата, наклонные к ней.

Упражнение 11Основание равнобедренного треугольника лежит в плоскости α (плоскость треугольника не совпадает с плоскостью α). Какой из углов больше: угол наклона боковой стороны к плоскости α или угол наклона высоты, опущенной на основание треугольника, к плоскости α?

Упражнение 12Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок AK, равный 3. Из точки K опущены перпендикуляры на стороны BC и CD. Перпендикуляр из точки K к стороне BC равен 6. Найдите углы, которые образуют эти перпендикуляры с плоскостью квадрата.