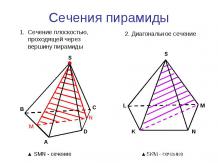
Презентация на тему: Угол между прямой и плоскостью

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ Подготовка к ЕГЭЗадания С2Учитель МОУ Бельская СОШТверской областиСильченкова С.Н.
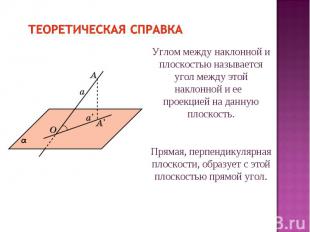
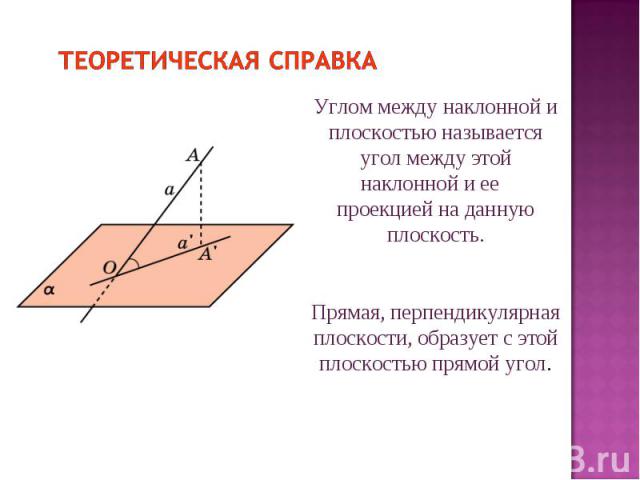
Теоретическая справка Углом между наклонной и плоскостью называется угол между этой наклонной и ее проекцией на данную плоскость. Прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол.
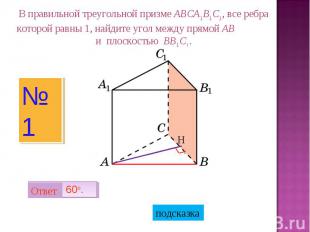
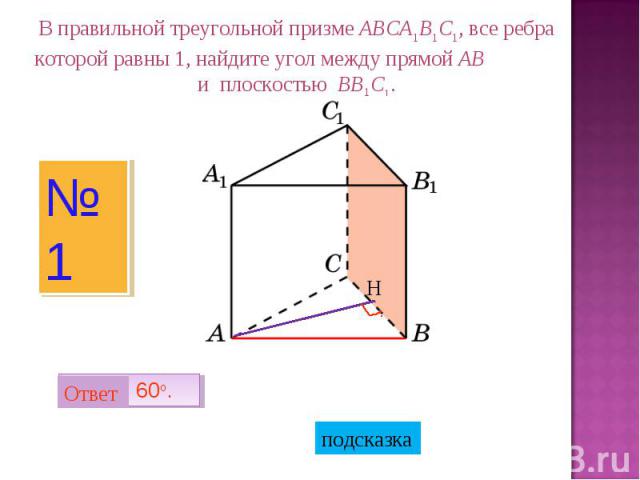
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямой AB и плоскостью BB1C1.
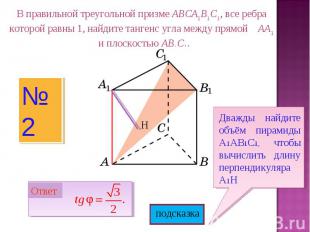
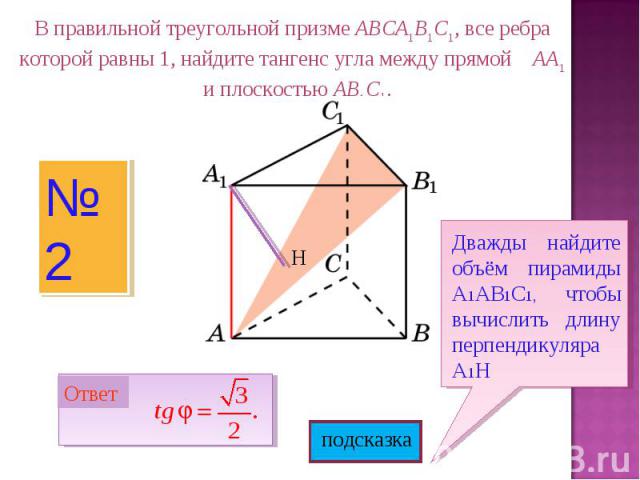
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью AB1C1.Дважды найдите объём пирамиды А1АВ1С1, чтобы вычислить длину перпендикуляра А1Н
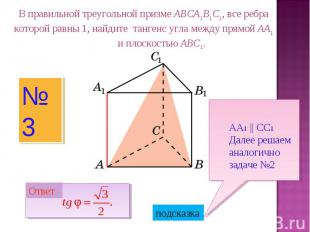
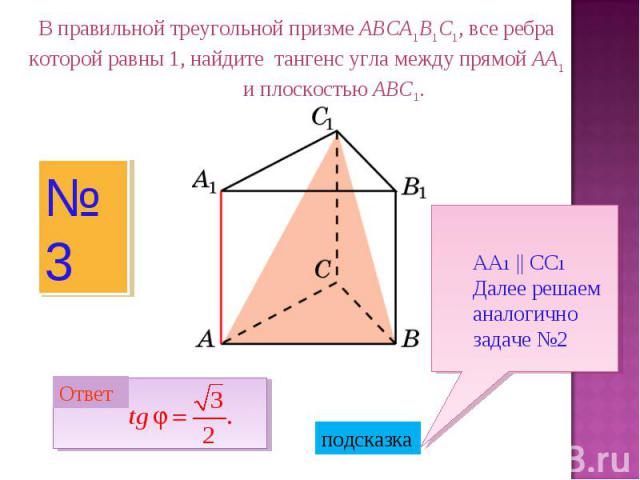
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между прямой AA1 и плоскостью ABC1.АА1 || СС1Далее решаем аналогично задаче №2
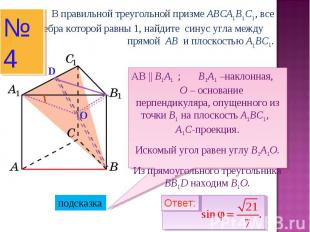
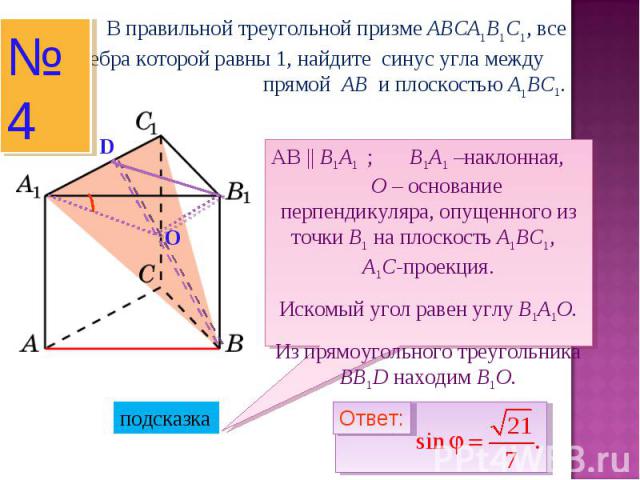
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите синус угла между прямой AB и плоскостью A1BC1.АВ || B1A1 ; B1A1 –наклонная, O – основание перпендикуляра, опущенного из точки B1 на плоскость A1BC1, A1C-проекция.Искомый угол равен углу B1A1O.Из прямоугольного треугольника BB1D находим B1O.
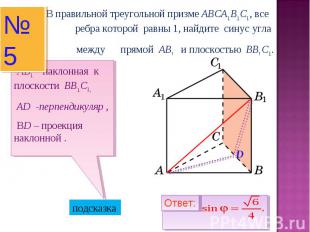
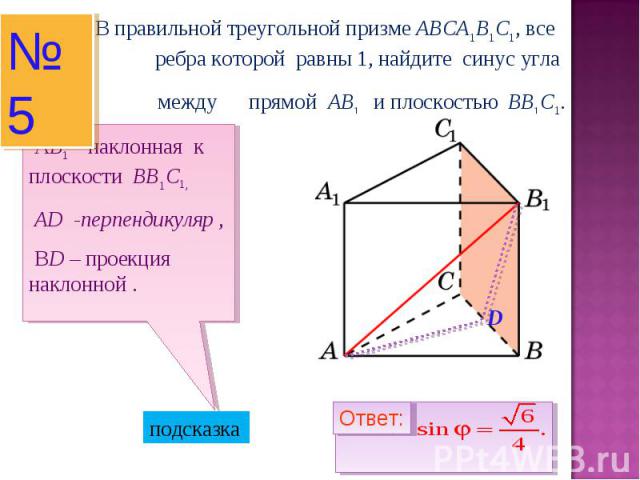
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите синус угла между прямой AB1 и плоскостью BB1C1. АB1 – наклонная к плоскости BB1C1, AD -перпендикуляр , ВD – проекция наклонной .
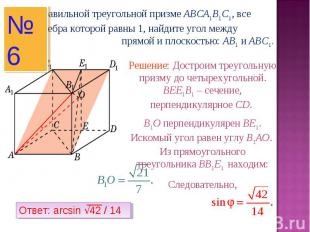
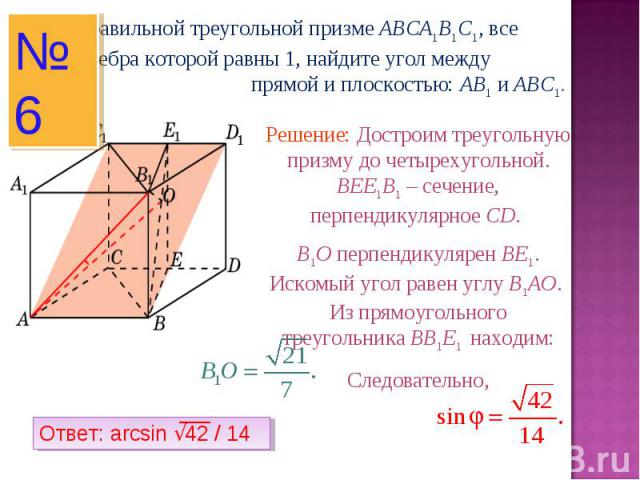
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямой и плоскостью: AB1 и ABC1.Решение: Достроим треугольную призму до четырехугольной. BEE1B1 – сечение, перпендикулярное CD. B1O перпендикулярен BE1. Искомый угол равен углу B1AO. Из прямоугольного треугольника BB1E1 находим:Следовательно,