Презентация на тему: Угол между прямыми. Угол между прямой и плоскостью

Угол между прямыми. Угол между прямой и плоскостью Геометрия, 10 класс.

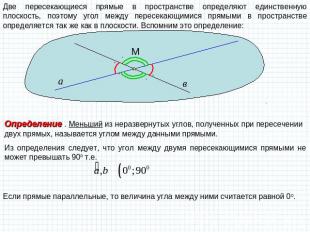
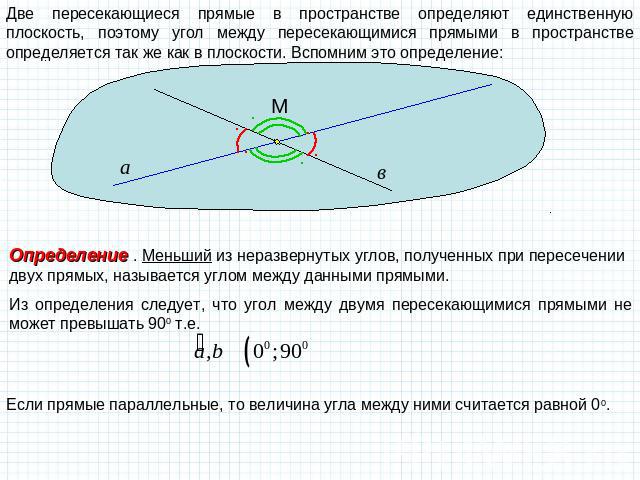
Две пересекающиеся прямые в пространстве определяют единственную плоскость, поэтому угол между пересекающимися прямыми в пространстве определяется так же как в плоскости. Вспомним это определение: Определение . Меньший из неразвернутых углов, полученных при пересечении двух прямых, называется углом между данными прямыми. Из определения следует, что угол между двумя пересекающимися прямыми не может превышать 900 т.е. Если прямые параллельные, то величина угла между ними считается равной 00.

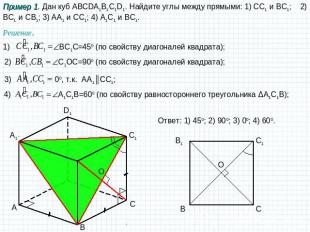
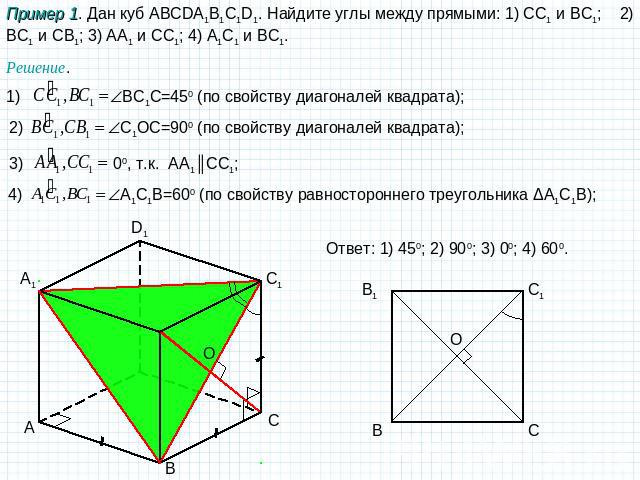
Пример 1. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1) CC1 и BC1; 2) BC1 и CB1; 3) AA1 и CC1; 4) A1C1 и BC1. Решение. 1) BC1C=450 (по свойству диагоналей квадрата); 2) C1ОC=900 (по свойству диагоналей квадрата); 3) 00, т.к. AA1║CC1; 4) A1C1B=600 (по свойству равностороннего треугольника ΔA1C1B); Ответ: 1) 450; 2) 900; 3) 00; 4) 600.

В общем случае, для нахождения угла между пересекающимися прямыми обычно рассматривают треугольник, в который входит интересующий нас угол. В прямоугольном треугольнике необходимо выразить какую-либо тригонометрическую функцию этого угла, в произвольном треугольнике – косинус данного угла (по следствию из теоремы косинусов). Далее сам угол находят с помощью обратных тригонометрических функций. Пример 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, AB=4 см, ВС=3 см, ВВ1=2 см. Найдите углы между прямыми: 1) CC1 и BC1; 2) BC1 и CB1; 3) AA1 и CC1; 3) A1C1 и BC1. Решение. 1) BC1C. Из ΔBC1C, С=900: tgBC1C=1,5 BC1C=arctg1,556018’; C1ОC. Из ΔOC1C, OC=OC1: О =1800–2· С1= = 1800–2arctg1,5 1800–112036’=67024’;(по теореме о сумме углов треугольника и свойству равнобедренного тр-ка) 3) 00, т.к. AA1║CC1; 4) A1C1B. Стороны ΔA1C1B находим из прямоугольных треугольников ΔA1C1D1, ΔAA1B , ΔCC1B по теореме Пифагора: A1C1=5 см, A1B= см, BC1= см. Теперь, по следствию из теоремы косинусов:

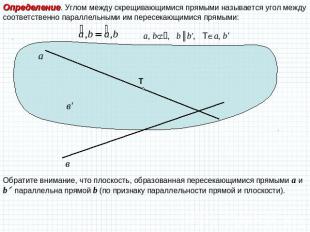
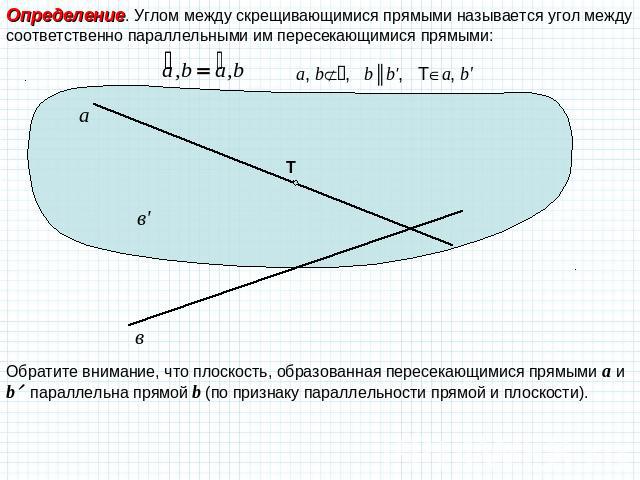
Определение. Углом между скрещивающимися прямыми называется угол между соответственно параллельными им пересекающимися прямыми: Обратите внимание, что плоскость, образованная пересекающимися прямыми a и b параллельна прямой b (по признаку параллельности прямой и плоскости).

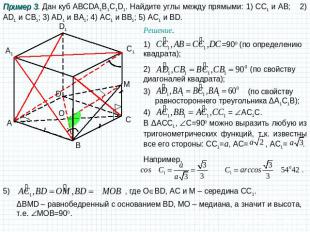
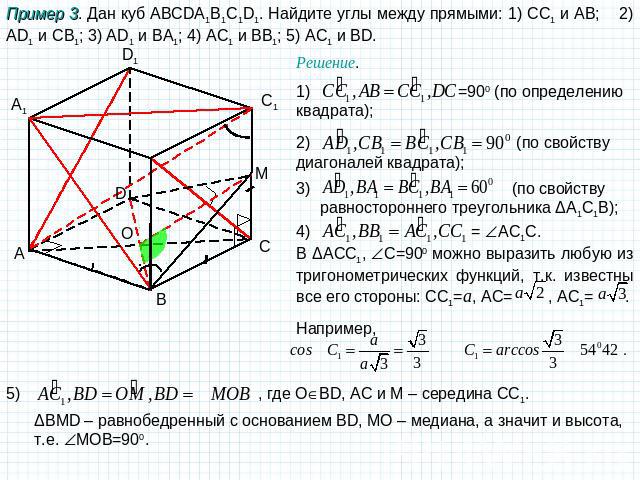
Пример 3. Дан куб ABCDA1B1C1D1. Найдите углы между прямыми: 1) CC1 и АB; 2) AD1 и CB1; 3) AD1 и BA1; 4) AC1 и BB1; 5) AC1 и BD. Решение. 1) =900 (по определению квадрата); 2) (по свойству диагоналей квадрата); 3) (по свойству равностороннего треугольника ΔA1C1B); 4) = AC1С. В ΔACC1, С=900 можно выразить любую из тригонометрических функций, т.к. известны все его стороны: СС1=а, АС= , AC1= . Например, ΔBMD – равнобедренный с основанием BD, МО – медиана, а значит и высота, т.е. MOB=900.

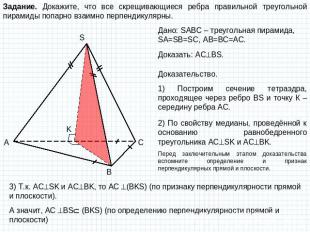
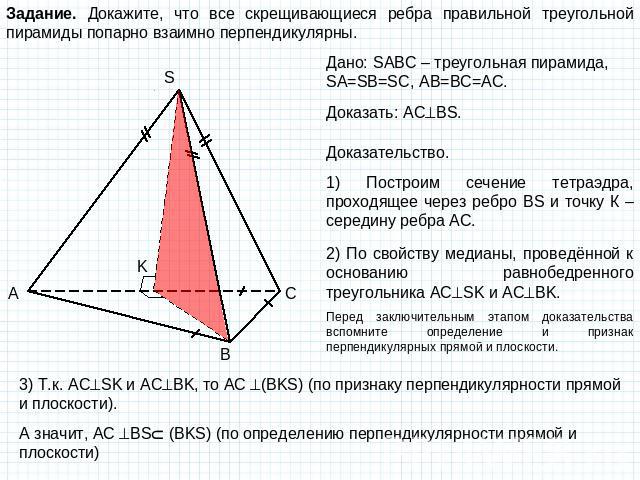
Задание. Докажите, что все скрещивающиеся ребра правильной треугольной пирамиды попарно взаимно перпендикулярны. Дано: SABC – треугольная пирамида, SA=SB=SC, AB=BC=AC. Доказать: ACBS. Доказательство. 1) Построим сечение тетраэдра, проходящее через ребро BS и точку К – середину ребра АС. 2) По свойству медианы, проведённой к основанию равнобедренного треугольника АСSK и ACBK. Перед заключительным этапом доказательства вспомните определение и признак перпендикулярных прямой и плоскости. 3) Т.к. АСSK и ACBK, то АС (BKS) (по признаку перпендикулярности прямой и плоскости). А значит, АС BS (BKS) (по определению перпендикулярности прямой и плоскости)

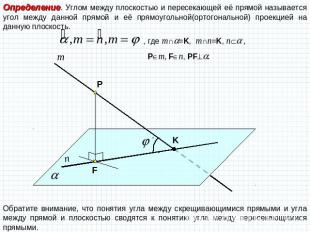
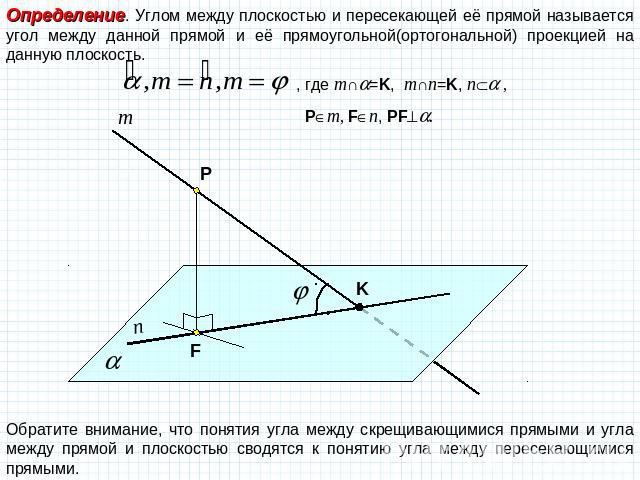
Определение. Углом между плоскостью и пересекающей её прямой называется угол между данной прямой и её прямоугольной(ортогональной) проекцией на данную плоскость. Обратите внимание, что понятия угла между скрещивающимися прямыми и угла между прямой и плоскостью сводятся к понятию угла между пересекающимися прямыми.

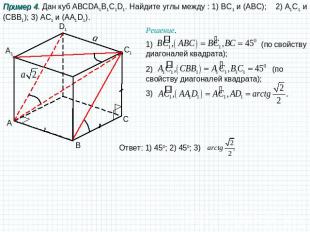
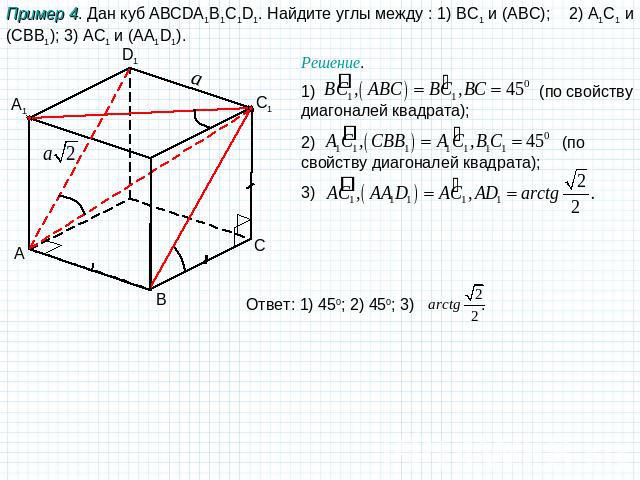
Пример 4. Дан куб ABCDA1B1C1D1. Найдите углы между : 1) BC1 и (АBC); 2) A1C1 и (CBB1); 3) AC1 и (AA1D1). Решение. 1) (по свойству диагоналей квадрата); 2) (по свойству диагоналей квадрата); 3) Ответ: 1) 450; 2) 450; 3) .