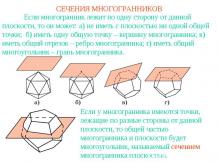
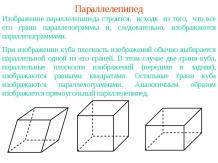
Презентация на тему: Определение параболы
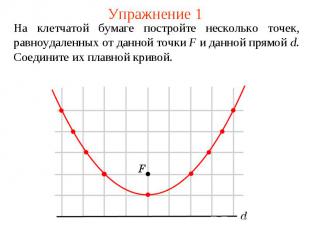
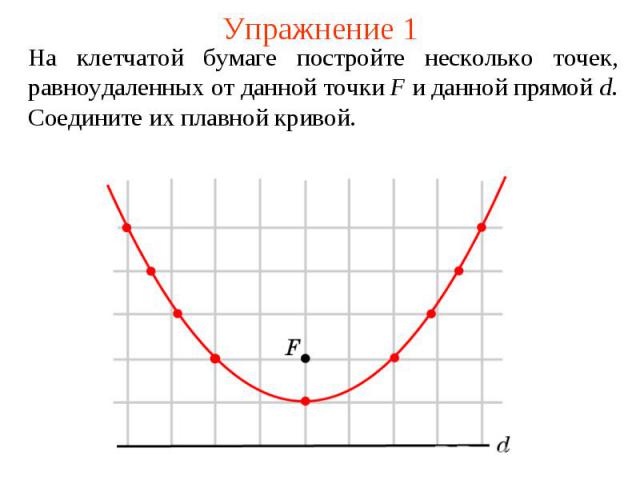
Упражнение 1На клетчатой бумаге постройте несколько точек, равноудаленных от данной точки F и данной прямой d. Соедините их плавной кривой.
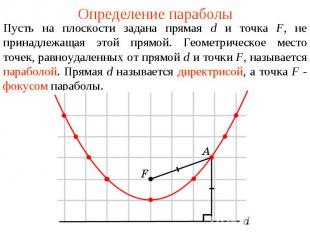
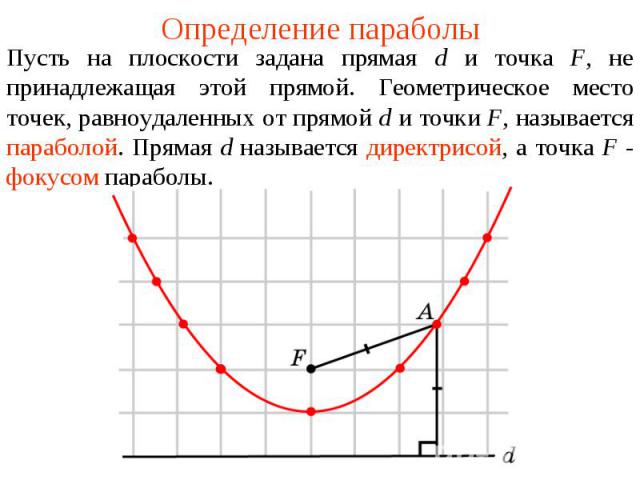
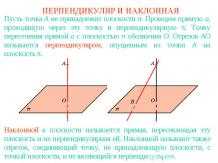
Определение параболыПусть на плоскости задана прямая d и точка F, не принадлежащая этой прямой. Геометрическое место точек, равноудаленных от прямой d и точки F, называется параболой. Прямая d называется директрисой, а точка F - фокусом параболы.
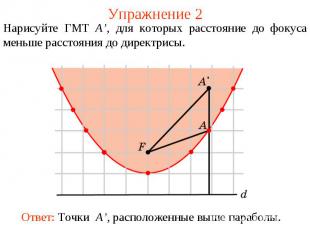
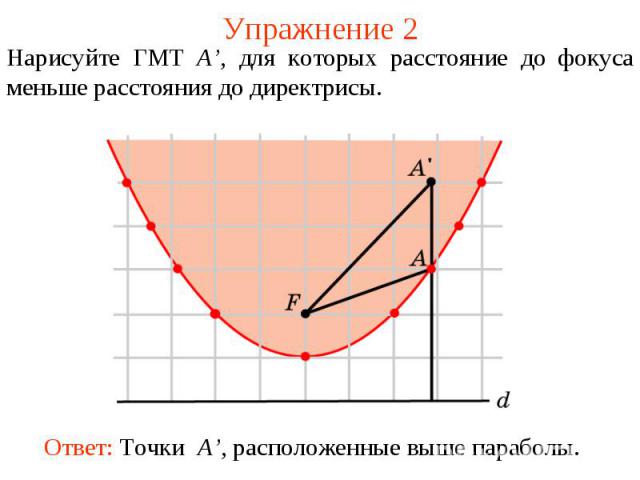
Упражнение 2Нарисуйте ГМТ A’, для которых расстояние до фокуса меньше расстояния до директрисы. Ответ: Точки A’, расположенные выше параболы.
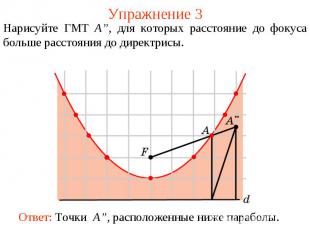
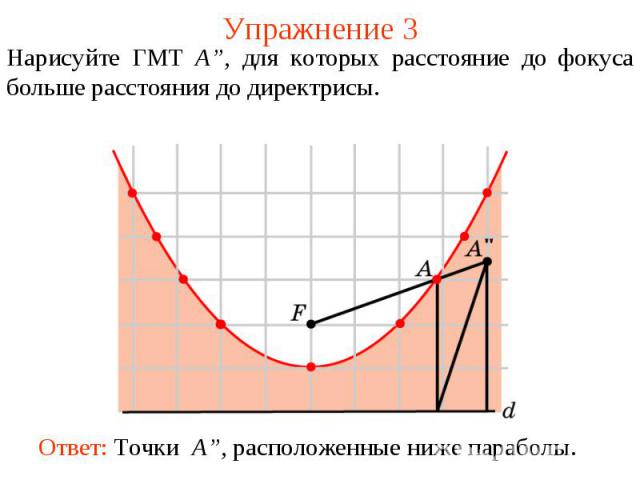
Упражнение 3Нарисуйте ГМТ A”, для которых расстояние до фокуса больше расстояния до директрисы.Ответ: Точки A”, расположенные ниже параболы.
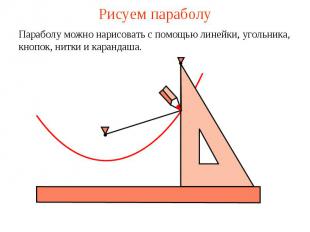
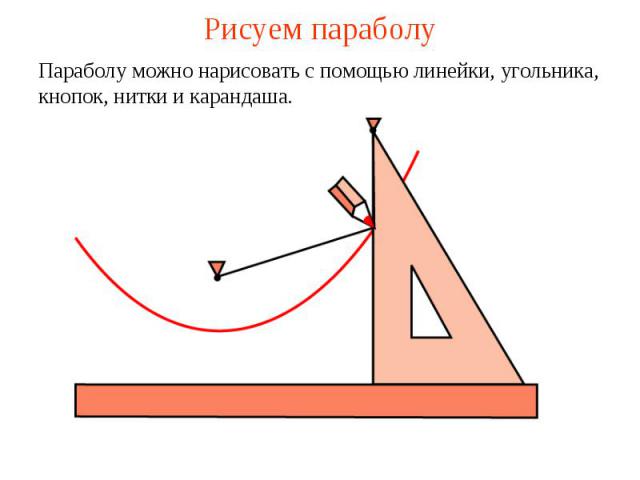
Рисуем параболуПараболу можно нарисовать с помощью линейки, угольника, кнопок, нитки и карандаша.
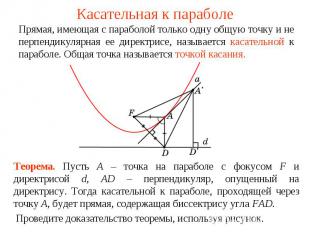
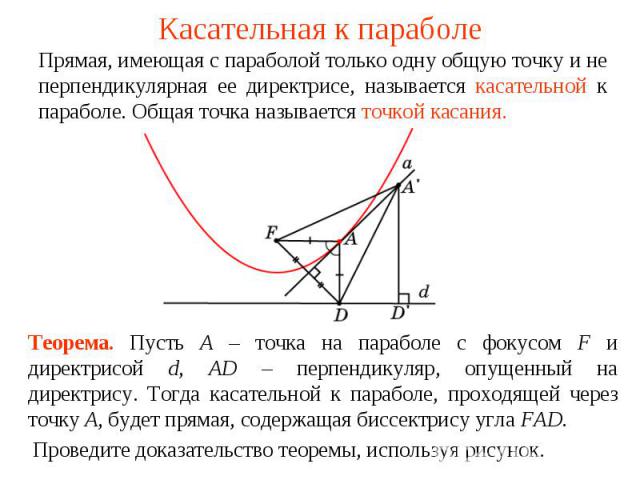
Касательная к параболеПрямая, имеющая с параболой только одну общую точку и не перпендикулярная ее директрисе, называется касательной к параболе. Общая точка называется точкой касания.Теорема. Пусть A – точка на параболе с фокусом F и директрисой d, АD – перпендикуляр, опущенный на директрису. Тогда касательной к параболе, проходящей через точку A, будет прямая, содержащая биссектрису угла FAD.Проведите доказательство теоремы, используя рисунок.
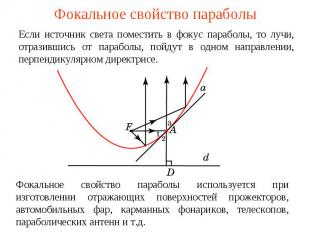
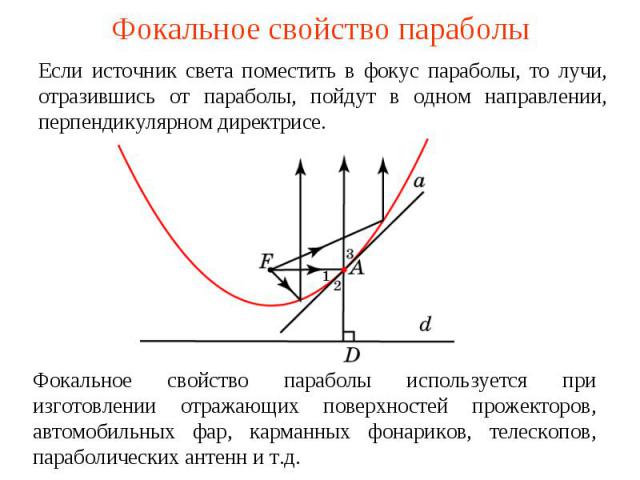
Фокальное свойство параболыЕсли источник света поместить в фокус параболы, то лучи, отразившись от параболы, пойдут в одном направлении, перпендикулярном директрисе.Фокальное свойство параболы используется при изготовлении отражающих поверхностей прожекторов, автомобильных фар, карманных фонариков, телескопов, параболических антенн и т.д.
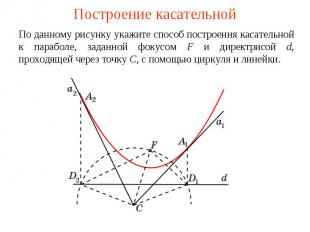
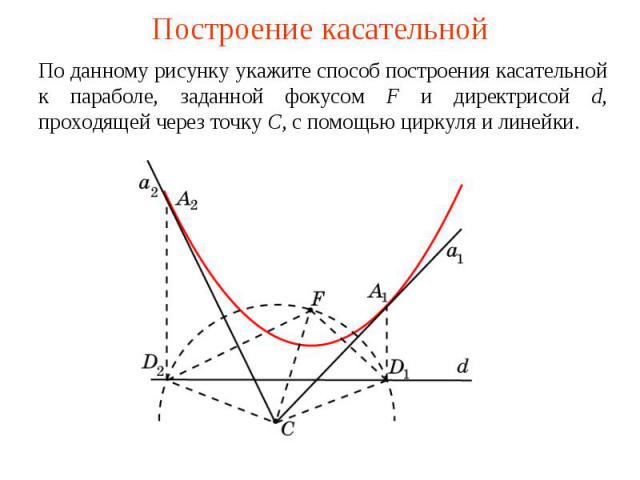
Построение касательнойПо данному рисунку укажите способ построения касательной к параболе, заданной фокусом F и директрисой d, проходящей через точку C, с помощью циркуля и линейки.
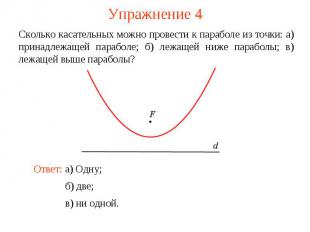
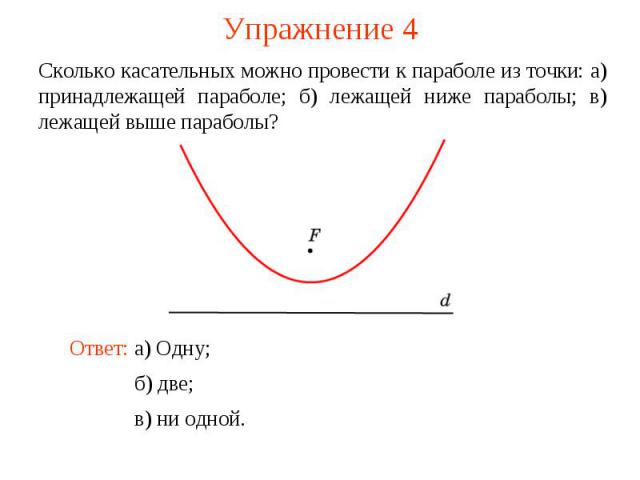
Упражнение 4Сколько касательных можно провести к параболе из точки: а) принадлежащей параболе; б) лежащей ниже параболы; в) лежащей выше параболы?

Упражнение 5Что будет происходить с параболой, если фокус: а) удаляется от директрисы; б) приближается к директрисе?Ответ: а) Ветви параболы разжимаются; б) ветви параболы сжимаются.
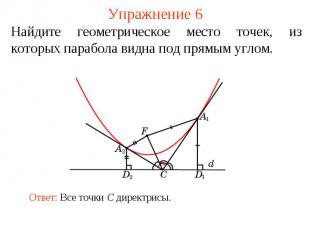
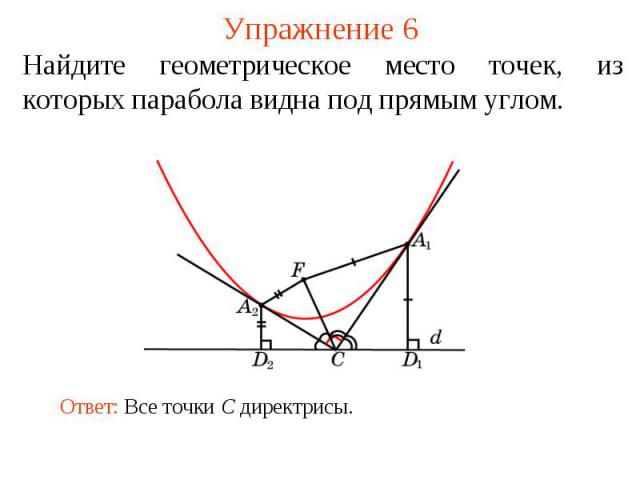
Упражнение 6Найдите геометрическое место точек, из которых парабола видна под прямым углом.Ответ: Все точки C директрисы.
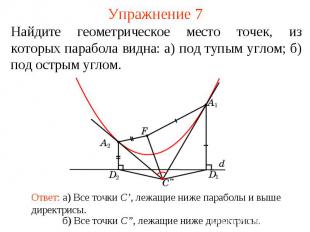
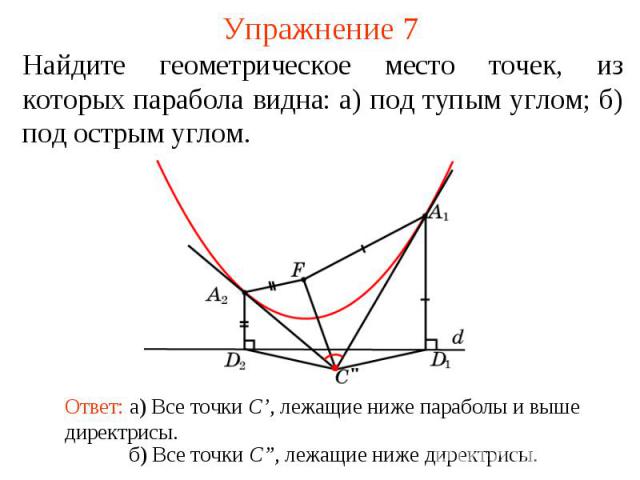
Упражнение 7Найдите геометрическое место точек, из которых парабола видна: а) под тупым углом; б) под острым углом.Ответ: а) Все точки C’, лежащие ниже параболы и выше директрисы.б) Все точки C”, лежащие ниже директрисы.