Презентация на тему: Выпуклые многогранные углы

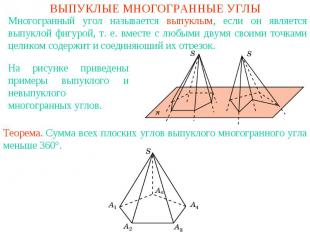
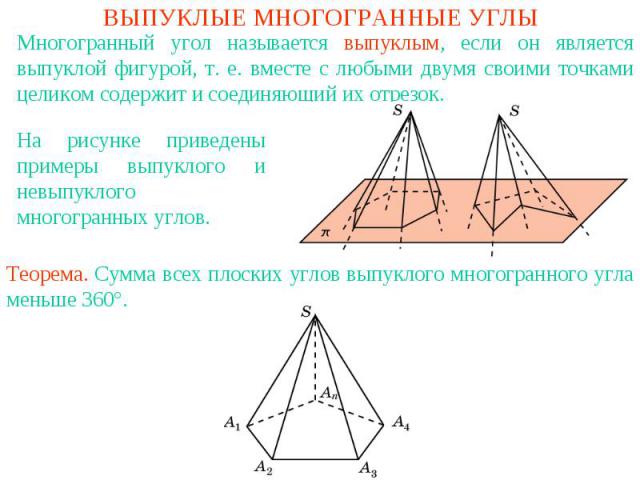
ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫМногогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок.На рисунке приведены примеры выпуклого и невыпуклого многогранных углов.Теорема. Сумма всех плоских углов выпуклого многогранного угла меньше 360°.

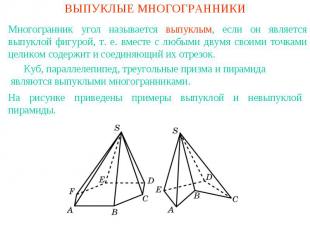
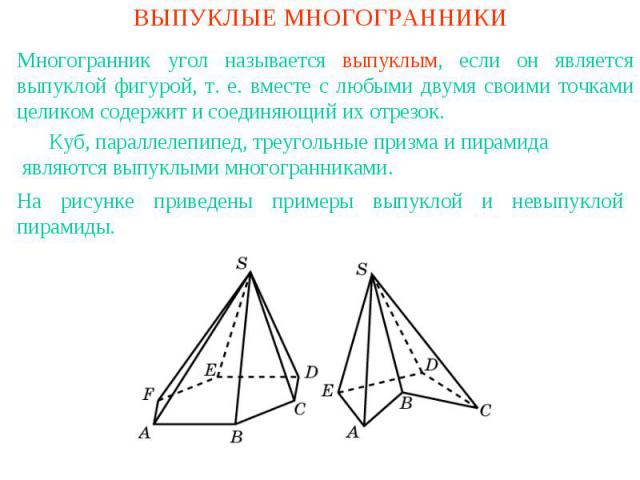
ВЫПУКЛЫЕ МНОГОГРАННИКИМногогранник угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок. Куб, параллелепипед, треугольные призма и пирамида являются выпуклыми многогранниками.На рисунке приведены примеры выпуклой и невыпуклой пирамиды.

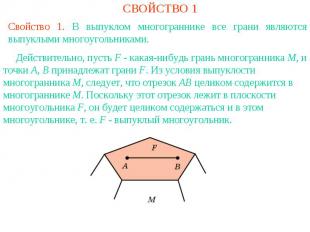
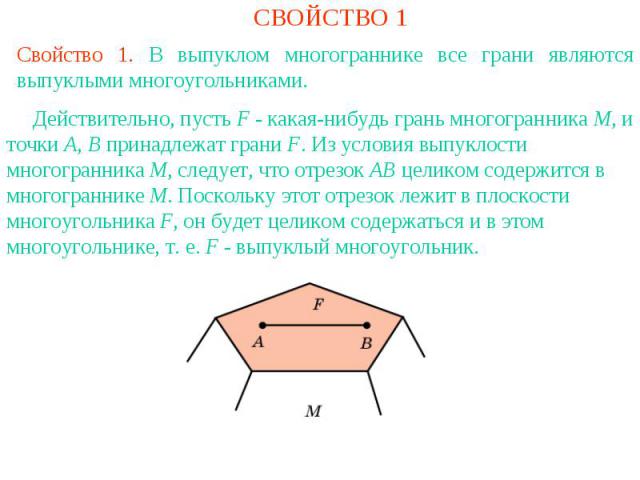
СВОЙСТВО 1Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками. Действительно, пусть F - какая-нибудь грань многогранника M, и точки A, B принадлежат грани F. Из условия выпуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т. е. F - выпуклый многоугольник.

СВОЙСТВО 2Свойство 2. Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.Действительно, пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т. е. такую его точку, которая не принадлежит ни одной грани многогранника M. Соединим точку S с вершинами многогранника M отрезками. Заметим, что в силу выпуклости многогранника M, все эти отрезки содержатся в M. Рассмотрим пирамиды с вершиной S, основаниями которых являются грани многогранника M. Эти пирамиды целиком содержатся в M, и все вместе составляют многогранник M.

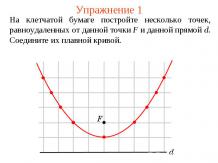
Упражнение 1На рисунке укажите выпуклые и невыпуклые плоские фигуры.Ответ: а), г) – выпуклые; б), в) – невыпуклые.

Упражнение 2Всегда ли пересечение выпуклых фигур является выпуклой фигурой?

Упражнение 3Всегда ли объединение выпуклых фигур является выпуклой фигурой?

Упражнение 4Можно ли составить выпуклый четырёхгранный угол с такими плоскими углами: а) 56о, 98о, 139о и 72о; б) 32о, 49о, 78о и 162о; в) 85о, 112о, 34о и 129о; г) 43о, 84о, 125о и 101о.

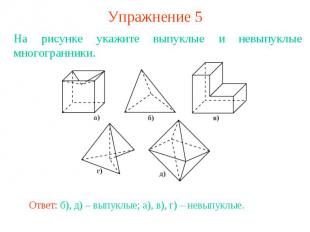
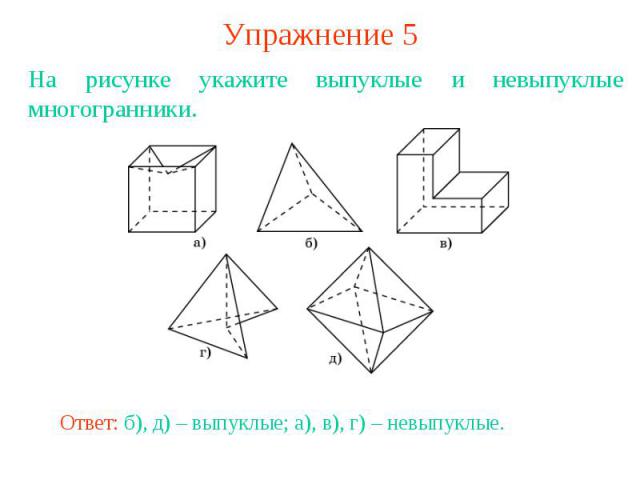
Упражнение 5На рисунке укажите выпуклые и невыпуклые многогранники.Ответ: б), д) – выпуклые; а), в), г) – невыпуклые.

Упражнение 6Может ли невыпуклый многоугольник быть гранью выпуклого многогранника?

Упражнение 7Может ли сечением выпуклого многогранника плоскостью быть невыпуклый многоугольник?

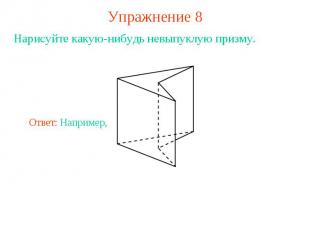
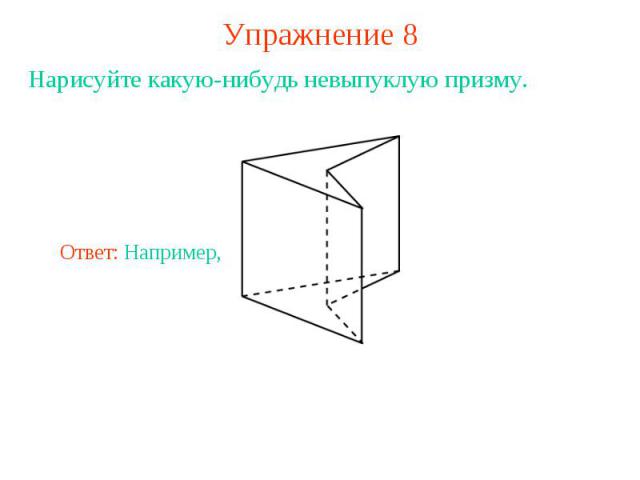
Упражнение 8Нарисуйте какую-нибудь невыпуклую призму.

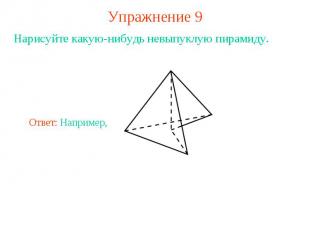
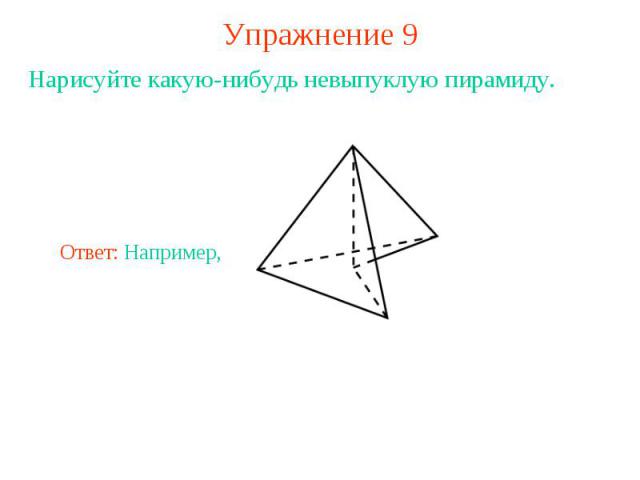
Упражнение 9Нарисуйте какую-нибудь невыпуклую пирамиду.

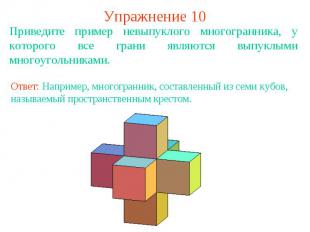
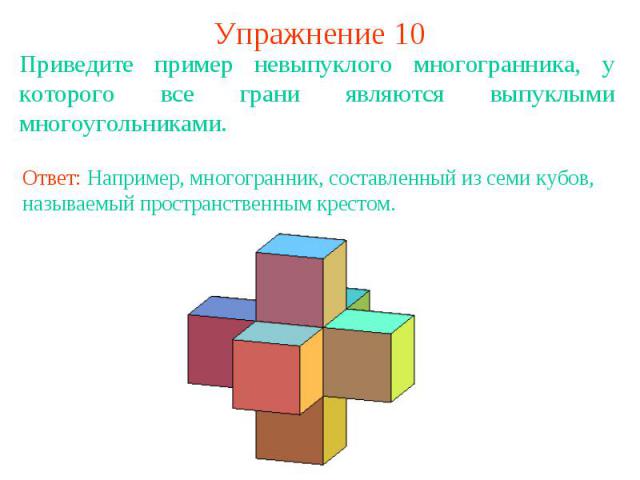
Упражнение 10Приведите пример невыпуклого многогранника, у которого все грани являются выпуклыми многоугольниками.Ответ: Например, многогранник, составленный из семи кубов, называемый пространственным крестом.