Презентация на тему: Определение графа

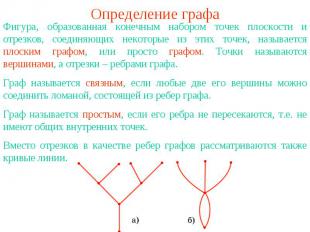
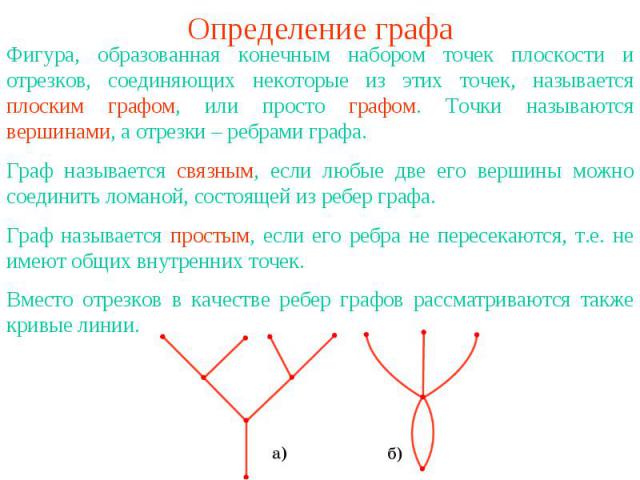
Определение графаФигура, образованная конечным набором точек плоскости и отрезков, соединяющих некоторые из этих точек, называется плоским графом, или просто графом. Точки называются вершинами, а отрезки – ребрами графа.Граф называется связным, если любые две его вершины можно соединить ломаной, состоящей из ребер графа.Граф называется простым, если его ребра не пересекаются, т.е. не имеют общих внутренних точек.Вместо отрезков в качестве ребер графов рассматриваются также кривые линии.

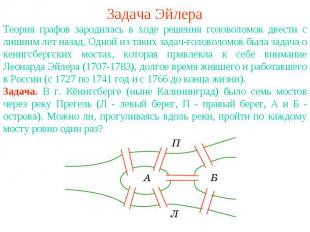
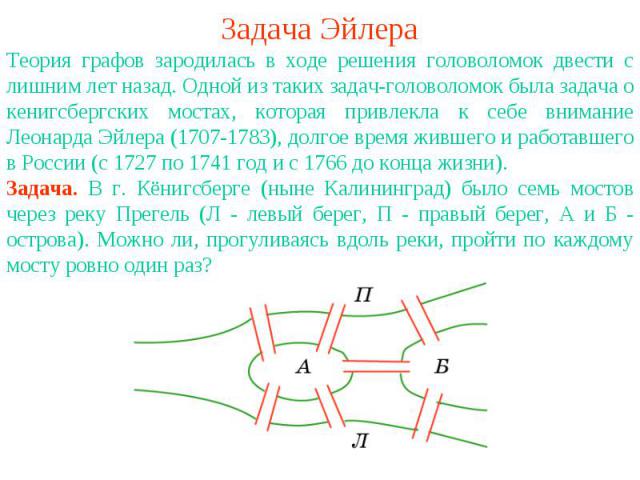
Задача ЭйлераТеория графов зародилась в ходе решения головоломок двести с лишним лет назад. Одной из таких задач-головоломок была задача о кенигсбергских мостах, которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое время жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца жизни).Задача. В г. Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (Л - левый берег, П - правый берег, А и Б - острова). Можно ли, прогуливаясь вдоль реки, пройти по каждому мосту ровно один раз?

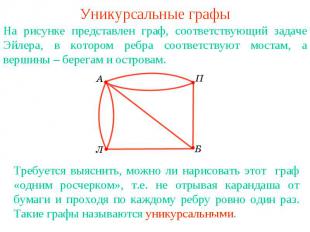
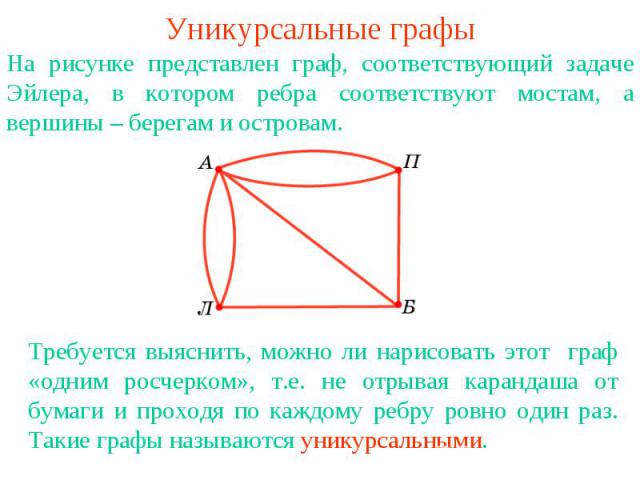
Уникурсальные графыНа рисунке представлен граф, соответствующий задаче Эйлера, в котором ребра соответствуют мостам, а вершины – берегам и островам. Требуется выяснить, можно ли нарисовать этот граф «одним росчерком», т.е. не отрывая карандаша от бумаги и проходя по каждому ребру ровно один раз. Такие графы называются уникурсальными.

ТеоремаИндексом вершины графа называется число ребер, сходящихся в этой вершине (ребра, с началом и концом в данной вершине считаются дважды). Теорема. Для уникурсального графа число вершин нечетного индекса равно нулю или двум. Доказательство. Если граф уникурсален, то у него есть начало и конец обхода. Остальные вершины имеют четный индекс, так как с каждым входом в такую вершину есть и выход. Если начало и конец не совпадают, то они являются единственными вершинами нечетного индекса. У начала выходов на один больше, чем входов, а у конца входов на один больше, чем выходов. Если начало совпадает с концом, то вершин с нечетным индексом нет. Верно и обратное: Если у связного графа число вершин нечетного индекса равно нулю или двум, то он является уникурсальным.

Решение задачи ЭйлераРешение задачи Эйлера. Найдем индексы вершин графа задачи Эйлера. Вершина А имеет индекс 5, Б - 3, П - 3 и Л - 3. Таким образом, мы имеем четыре вершины нечетного индекса, и, следовательно, данный граф не является уникурсальным. Значит, нельзя пройти по каждому из семи мостов только один раз.

Вопрос 1Какая фигура называется графом? Ответ: Графом называется фигура, образованная конечным набором точек плоскости и отрезков, соединяющих некоторые из этих точек.

Вопрос 2Какой граф называется уникурсальным? Ответ: Граф называется уникурсальным, если его можно ли нарисовать «одним росчерком», т.е. не отрывая карандаша от бумаги и проходя по каждому ребру ровно один раз.

Вопрос 3Что называется индексом вершины графа? Ответ: Индексом вершины графа называется число ребер, сходящихся в этой вершине (ребра, с началом и концом в данной вершине считаются дважды).

Вопрос 4Что можно сказать об индексах вершин уникурсального графа?Ответ: Для уникурсального графа число вершин нечетного индекса равно нулю или двум.

Упражнение 1В графе 4 вершин, каждая из которых имеет индекс 3. Сколько у него ребер? Нарисуйте такой граф.

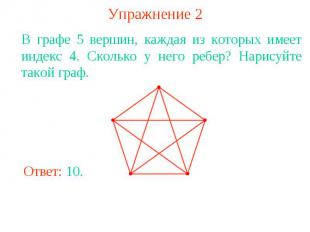
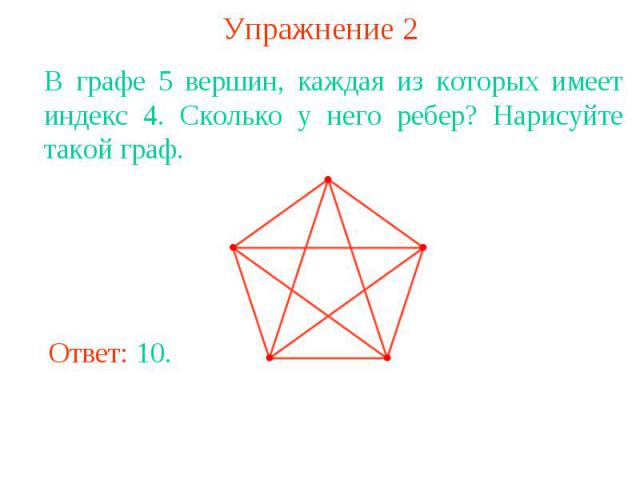
Упражнение 2В графе 5 вершин, каждая из которых имеет индекс 4. Сколько у него ребер? Нарисуйте такой граф.

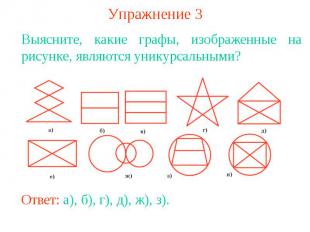
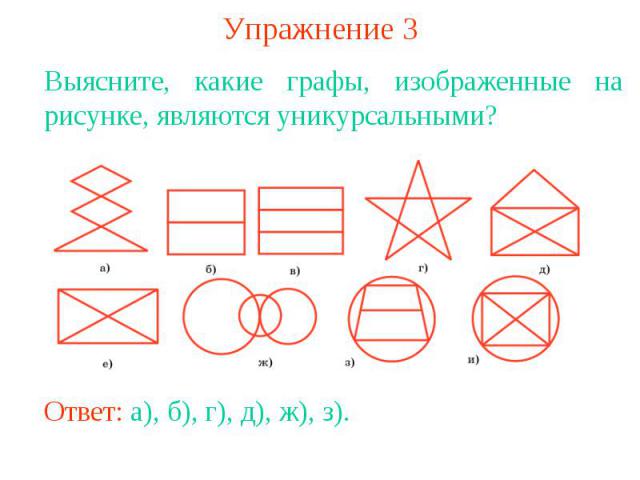
Упражнение 3Выясните, какие графы, изображенные на рисунке, являются уникурсальными?

Упражнение 4Может ли граф иметь: а) одну вершину нечетного индекса; б) две вершины нечетного индекса; в) три вершины нечетного индекса; г) четыре вершины нечетного индекса?

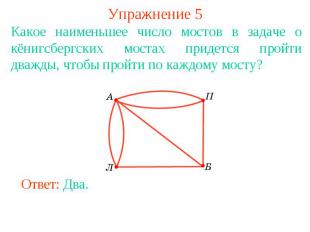
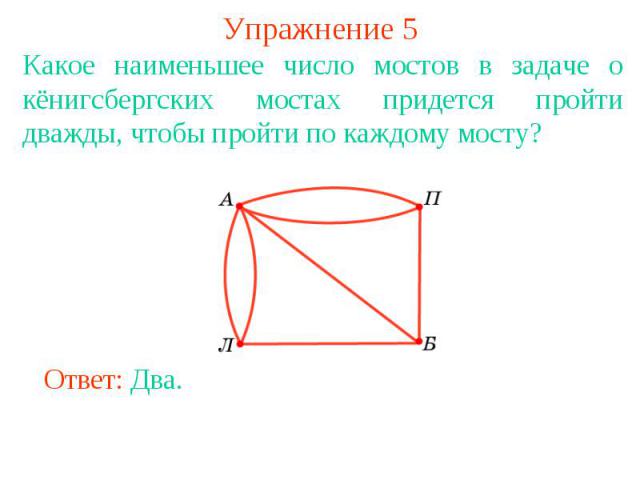
Упражнение 5Какое наименьшее число мостов в задаче о кёнигсбергских мостах придется пройти дважды, чтобы пройти по каждому мосту?

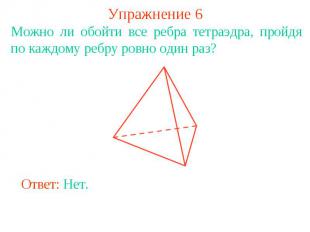
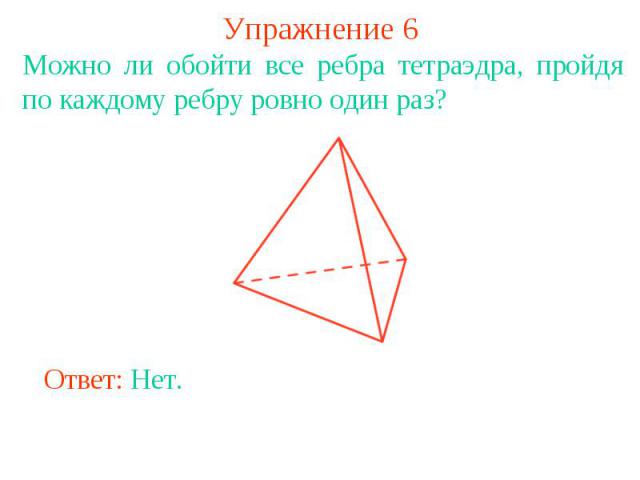
Упражнение 6Можно ли обойти все ребра тетраэдра, пройдя по каждому ребру ровно один раз?

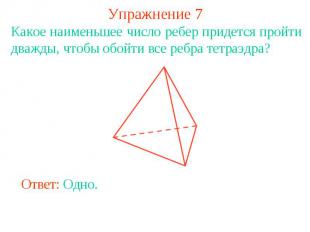
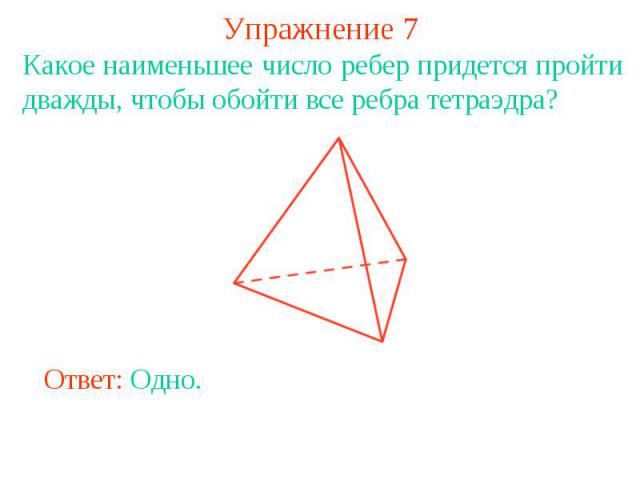
Упражнение 7Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра?

Упражнение 8Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра тетраэдра и вернуться в исходную вершину?

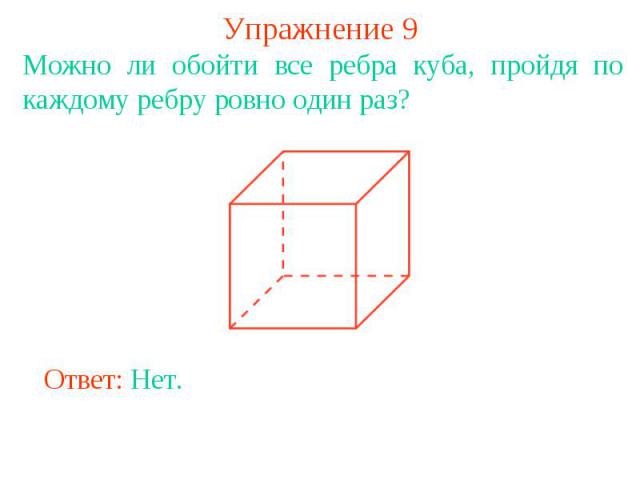
Упражнение 9Можно ли обойти все ребра куба, пройдя по каждому ребру ровно один раз?

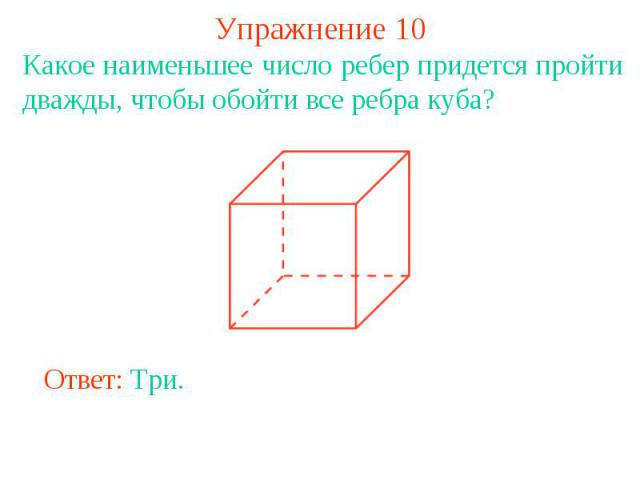
Упражнение 10Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба?

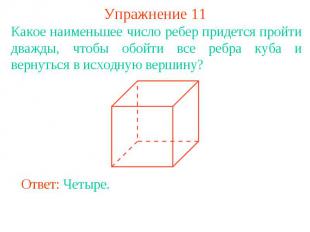
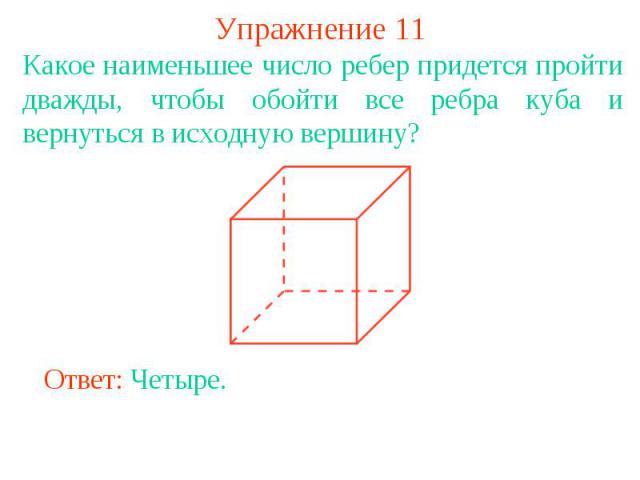
Упражнение 11Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра куба и вернуться в исходную вершину?

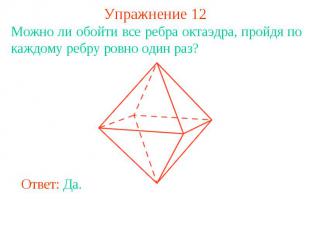
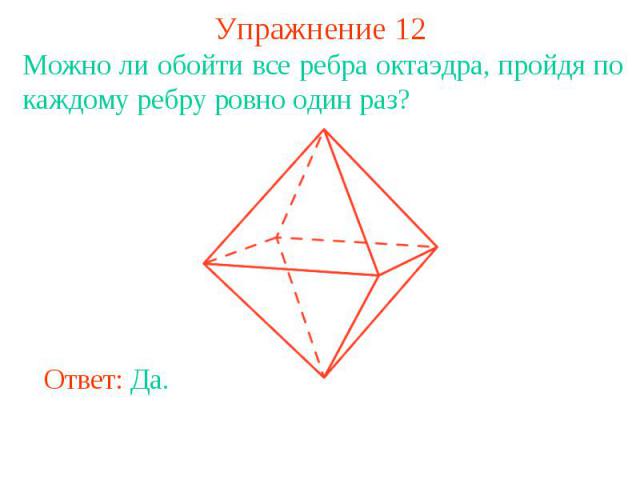
Упражнение 12Можно ли обойти все ребра октаэдра, пройдя по каждому ребру ровно один раз?

Упражнение 13Можно ли обойти все ребра икосаэдра, пройдя по каждому ребру ровно один раз?

Упражнение 14Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра?

Упражнение 15Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра икосаэдра и вернуться в исходную вершину?

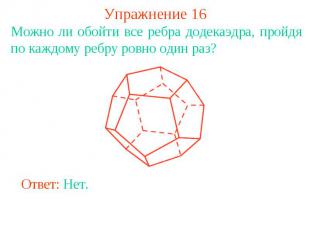
Упражнение 16Можно ли обойти все ребра додекаэдра, пройдя по каждому ребру ровно один раз?

Упражнение 17Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра?

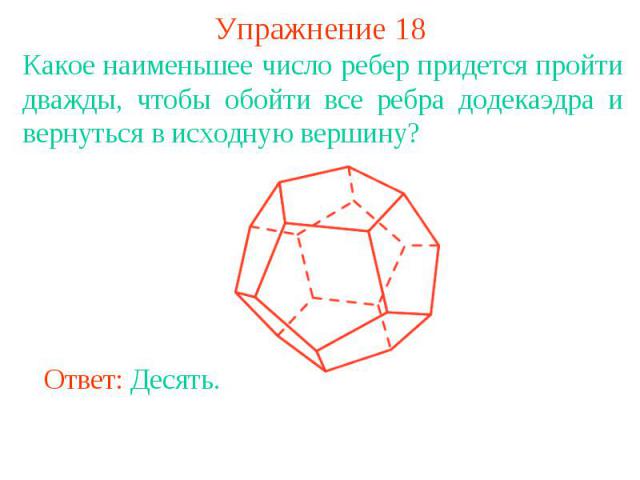
Упражнение 18Какое наименьшее число ребер придется пройти дважды, чтобы обойти все ребра додекаэдра и вернуться в исходную вершину?

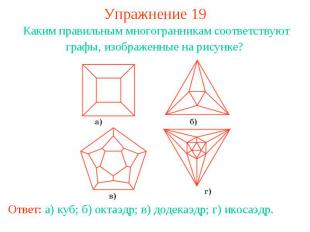
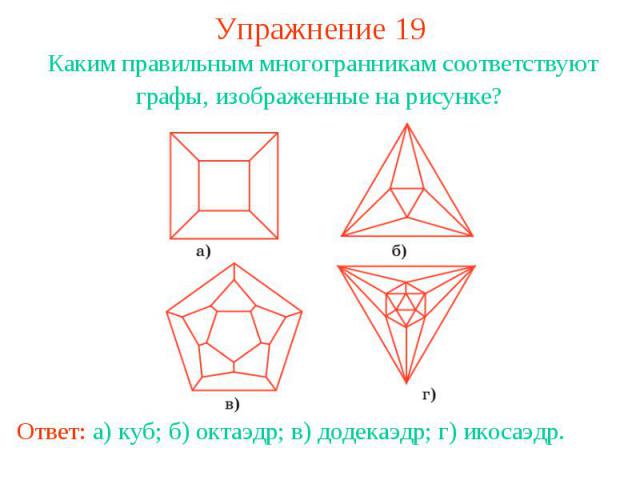
Упражнение 19Каким правильным многогранникам соответствуют графы, изображенные на рисунке? Ответ: а) куб; б) октаэдр; в) додекаэдр; г) икосаэдр.