Презентация на тему: Теорема эйлера

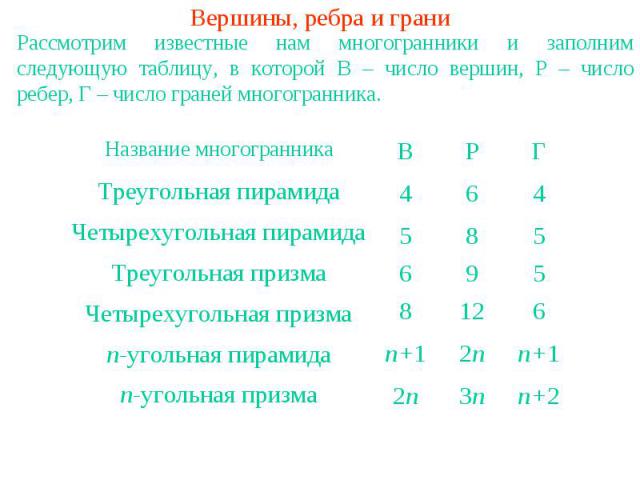
Вершины, ребра и граниРассмотрим известные нам многогранники и заполним следующую таблицу, в которой В – число вершин, Р – число ребер, Г – число граней многогранника.

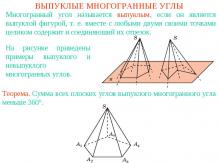
ТЕОРЕМА ЭЙЛЕРАИз приведенной таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо не только для рассмотренных многогранников, но и для произвольного выпуклого многогранника. Впервые это свойство выпуклых многогранников было доказано Леонардом Эйлером в 1752 году и получило название теоремы Эйлера. Теорема Эйлера. Для любого выпуклого многогранника имеет место равенствоВ - Р + Г = 2,где В - число вершин, Р - число ребер и Г - число граней данного многогранника.
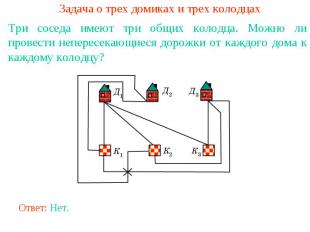
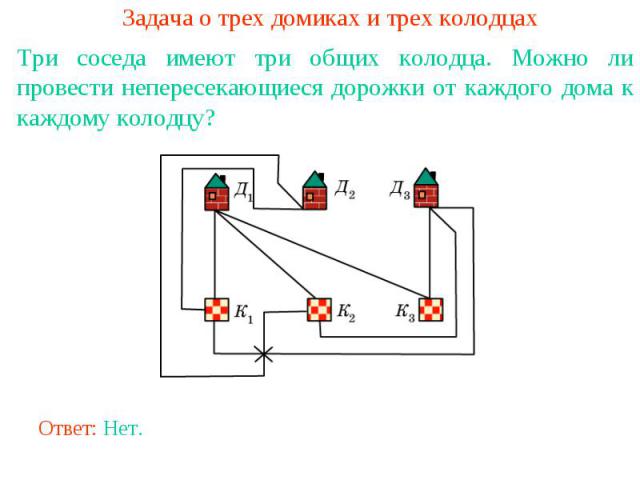
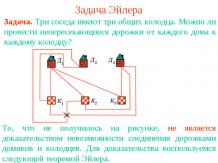
Задача о трех домиках и трех колодцахТри соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?

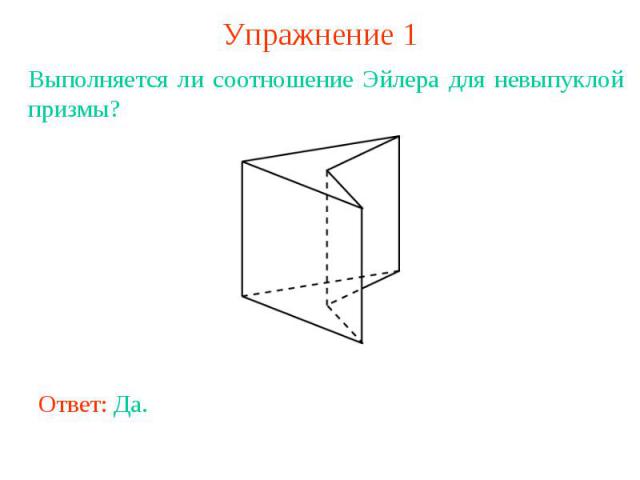
Упражнение 1Выполняется ли соотношение Эйлера для невыпуклой призмы?

Упражнение 2Выполняется ли соотношение Эйлера для невыпуклой пирамиды?
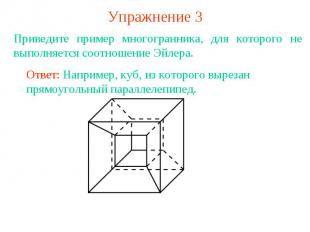
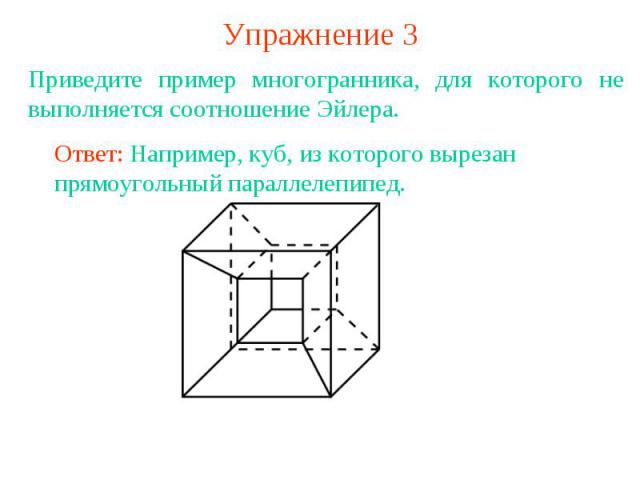
Упражнение 3Приведите пример многогранника, для которого не выполняется соотношение Эйлера.Ответ: Например, куб, из которого вырезан прямоугольный параллелепипед.

Упражнение 4Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет: а) 12 ребер; б) 15 ребер?

Упражнение 5Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин и граней, если число ребер равно: а) 12; б) 15?

Упражнение 6Гранями выпуклого многогранника являются только четырехугольники. Сколько у него вершин и граней, если число ребер равно 12? Приведите пример такого многогранника.

Упражнение 7В каждой вершине выпуклого многогранника сходится по четыре ребра. Сколько он имеет вершин и граней, если число ребер равно 12? Приведите пример такого многогранника.
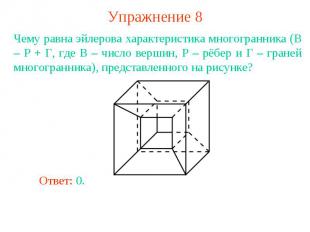
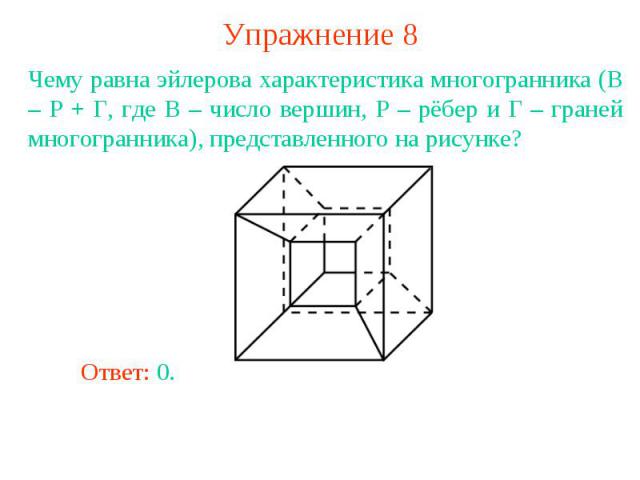
Упражнение 8Чему равна эйлерова характеристика многогранника (В – Р + Г, где В – число вершин, Р – рёбер и Г – граней многогранника), представленного на рисунке?

Упражнение 9Как изменится число вершин, рёбер и граней выпуклого многогранника, если к одной из его граней пристроить пирамиду? Изменится ли В – Р + Г?Ответ: Пусть пристроена n-угольная пирамида, тогда количество вершин станет (В+1), рёбер - (Р+n), граней - (Г+n). В – Р + Г не изменится.

Упражнение 10Как изменится число вершин, рёбер и граней выпуклого многогранника, если от него отсечь один из многогранных углов? Изменится ли В – Р + Г?Ответ: Пусть отсекли m-гранный угол, тогда количество вершин будет (В+m-1), рёбер - (Р+m), граней - (Г+1). В – Р + Г не изменится.