Презентация на тему: Прямоугольник

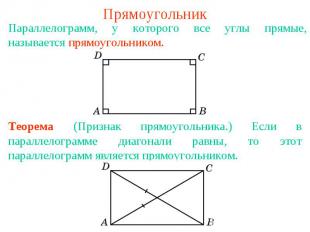
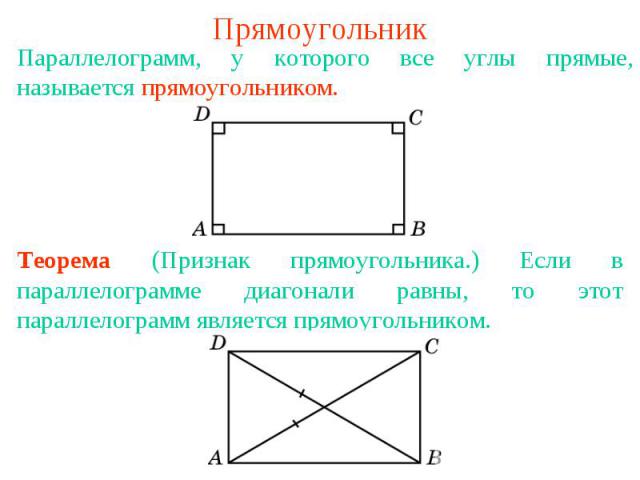
ПрямоугольникПараллелограмм, у которого все углы прямые, называется прямоугольником. Теорема (Признак прямоугольника.) Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

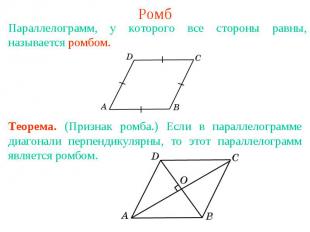
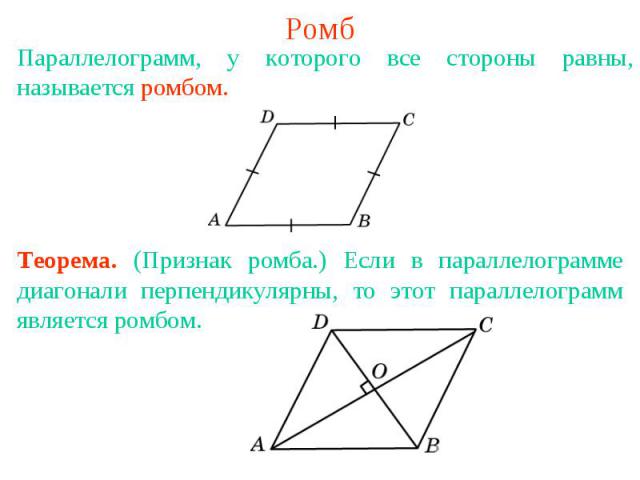
РомбПараллелограмм, у которого все стороны равны, называется ромбом. Теорема. (Признак ромба.) Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом.

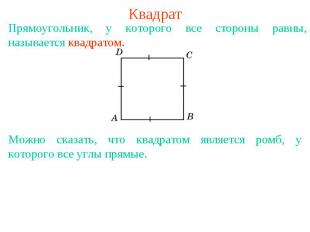
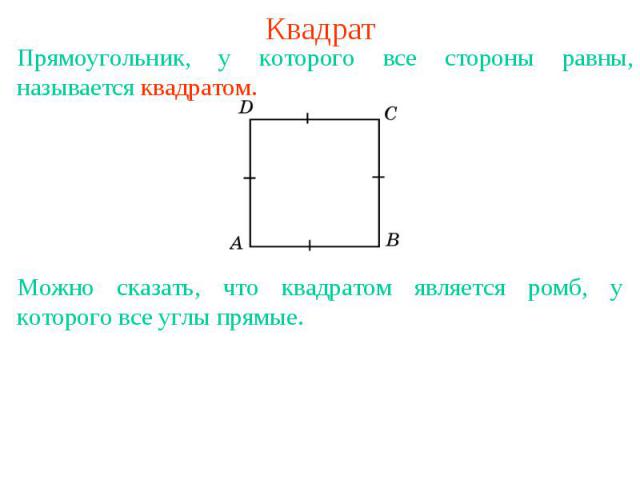
КвадратПрямоугольник, у которого все стороны равны, называется квадратом. Можно сказать, что квадратом является ромб, у которого все углы прямые.

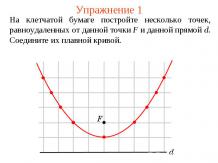
Упражнение 1Из точки D, принадлежащей гипотенузе AB прямоугольного треугольника ABC, проведены две прямые, параллельные катетам. Сумма периметров получившихся треугольников AKD и DLB равна 10 см. Найдите периметр данного треугольника ABC.

Упражнение 2Два равных прямоугольных треугольника приложили один к другому таким образом, что их гипотенузы совпали, а неравные острые углы приложились один к другому. Какой при этом получился четырехугольник?

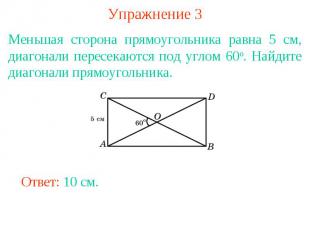
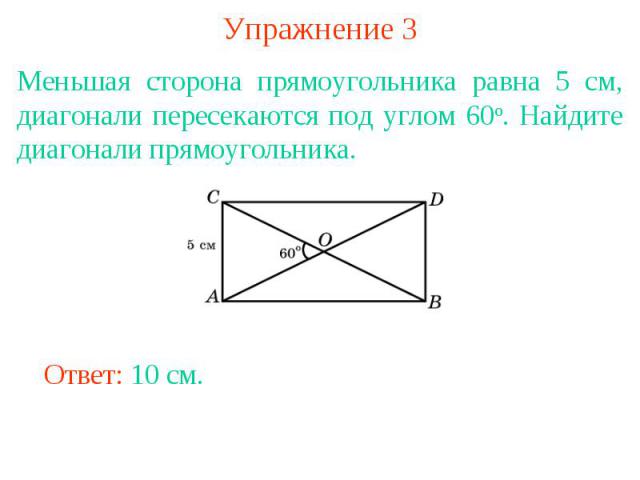
Упражнение 3Меньшая сторона прямоугольника равна 5 см, диагонали пересекаются под углом 60о. Найдите диагонали прямоугольника.

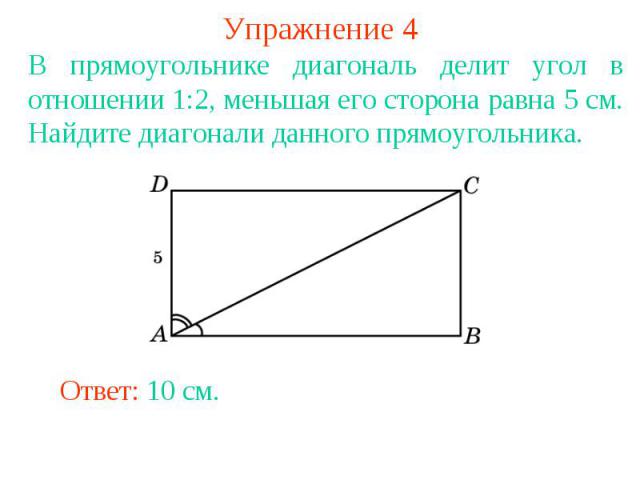
Упражнение 4В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 5 см. Найдите диагонали данного прямоугольника.

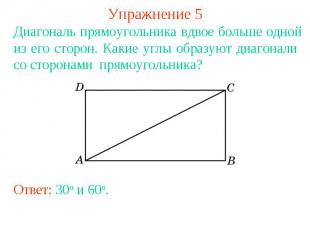
Упражнение 5Диагональ прямоугольника вдвое больше одной из его сторон. Какие углы образуют диагонали со сторонами прямоугольника?

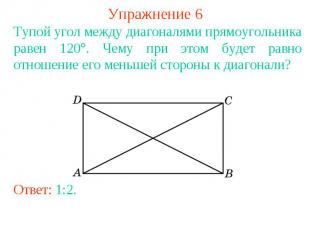
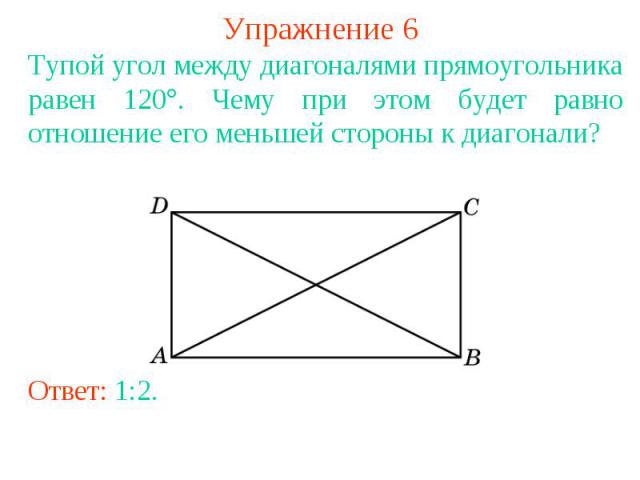
Упражнение 6Тупой угол между диагоналями прямоугольника равен 120. Чему при этом будет равно отношение его меньшей стороны к диагонали?

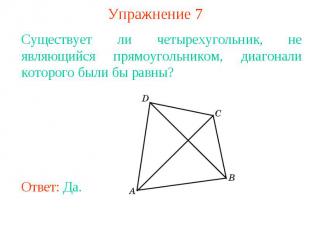
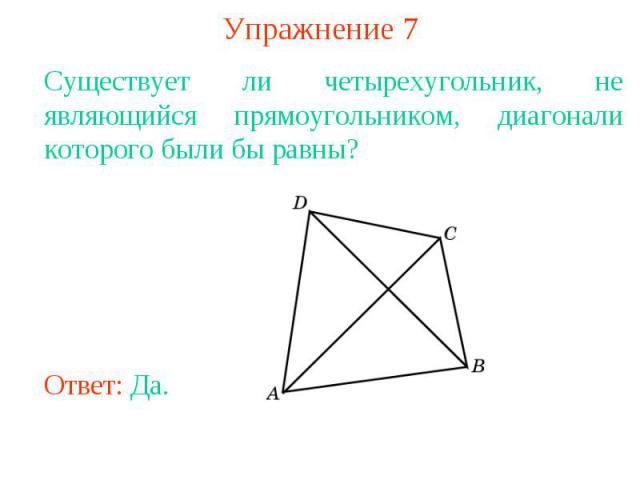
Упражнение 7Существует ли четырехугольник, не являющийся прямоугольником, диагонали которого были бы равны?

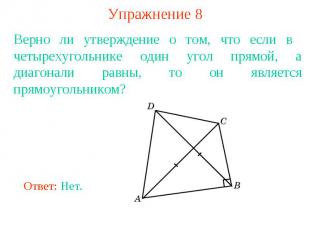
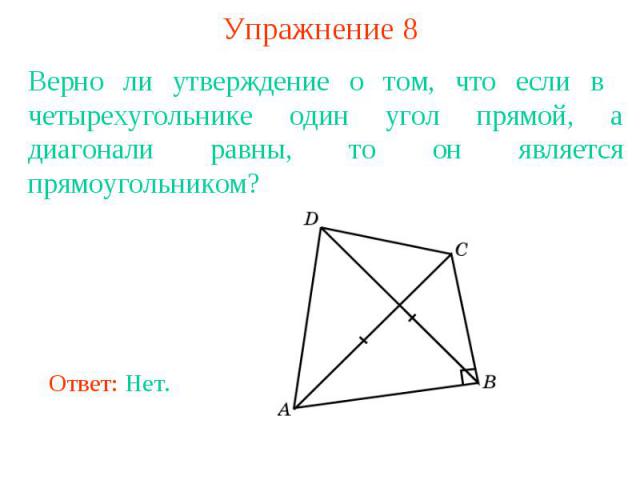
Упражнение 8Верно ли утверждение о том, что если в четырехугольнике один угол прямой, а диагонали равны, то он является прямоугольником?

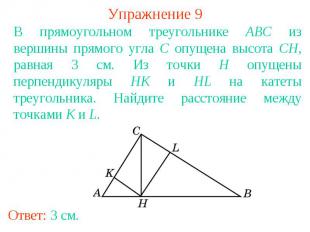
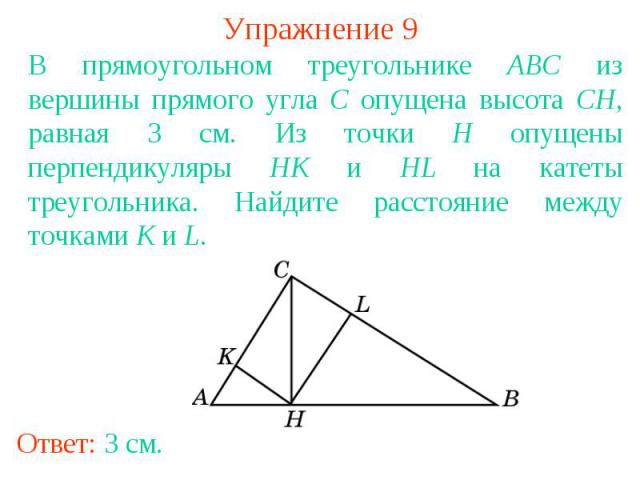
Упражнение 9В прямоугольном треугольнике ABC из вершины прямого угла C опущена высота CH, равная 3 см. Из точки H опущены перпендикуляры HK и HL на катеты треугольника. Найдите расстояние между точками K и L.

Упражнение 10Найдите диагонали прямоугольника, если его периметр равен 34 см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 30 см.

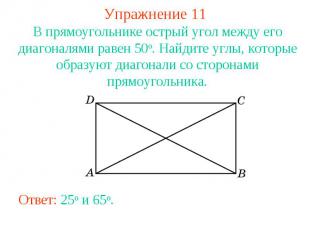
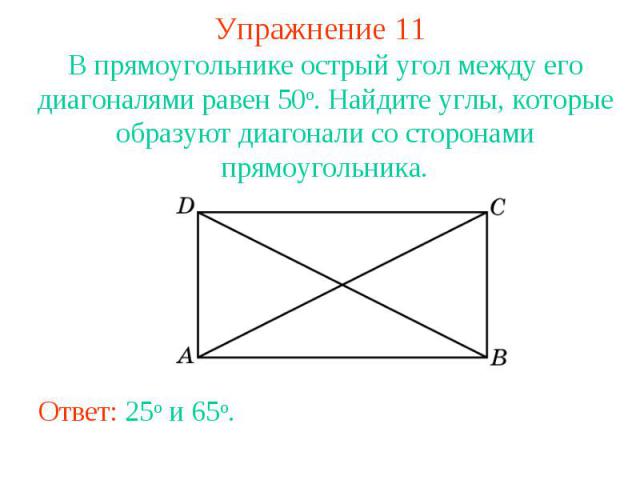
Упражнение 11В прямоугольнике острый угол между его диагоналями равен 50о. Найдите углы, которые образуют диагонали со сторонами прямоугольника.

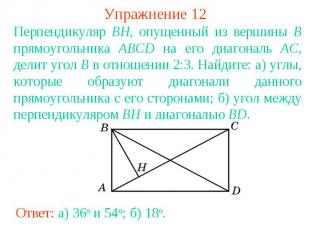
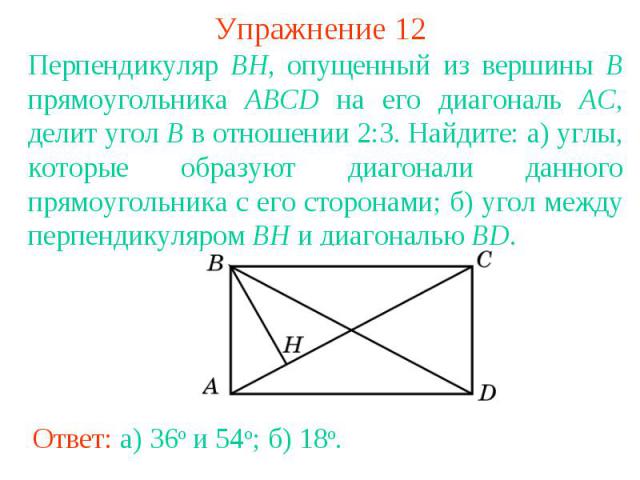
Упражнение 12Перпендикуляр BH, опущенный из вершины B прямоугольника ABCD на его диагональ AC, делит угол B в отношении 2:3. Найдите: а) углы, которые образуют диагонали данного прямоугольника с его сторонами; б) угол между перпендикуляром BH и диагональю BD.

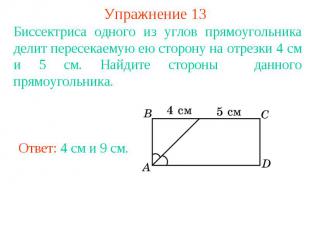
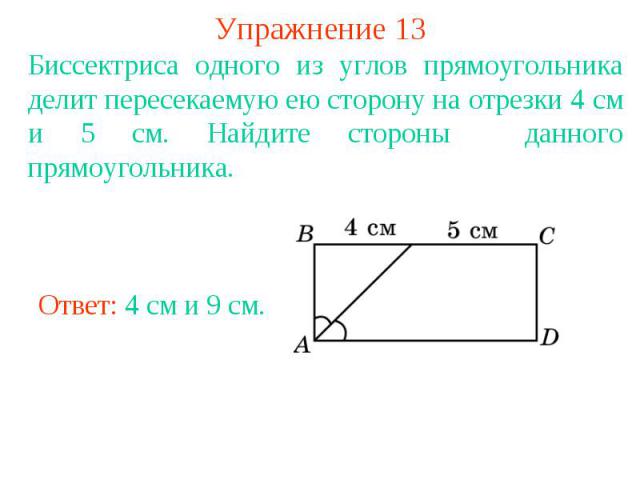
Упражнение 13Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону на отрезки 4 см и 5 см. Найдите стороны данного прямоугольника.

Упражнение 14Чему равна меньшая диагональ ромба со стороной а и острым углом в 60о?

Упражнение 15В ромбе одна из диагоналей равна его стороне. Найдите углы ромба.

Упражнение 16Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба.

Упражнение 17Чему равен угол между: а) диагоналями квадрата: б) диагональю и стороной квадрата?

Упражнение 18В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 5 см. Найдите периметр этого квадрата.