Презентация на тему: Центральная симметрия

Центральная симметрия
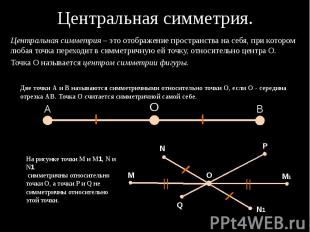
Центральная симметрия.

Теорема. Центральная симметрия – движение. Доказательство: Пусть при центральной симметрии с центром в точке О точки X и Y отобразились на X' и Y'. Тогда, как ясно из определения центральной симметрии, OX' = -OX, OY' = -OY. Вместе с тем XY = OY - OX, X'Y' = OY' - OX' Поэтому имеем: X'Y' = -OY + OX = -XY Отсюда выходит, что центральная симметрия является движением, изменяющим направление на противоположное и наоборот, движение, изменяющее направление на противоположное, есть центральная симметрия.

Центральная симметрия в прямоугольной системе координат. Если в прямоугольной системе координат точка А имеет координаты (x0;y0), то координаты (-x0;-y0) точки А1, симметричной точке А относительно начала координат, выражаются формулами: x0 = -x0 y0 = -y0

Примеры из жизни. Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей. Центральная симметрия встречается в форме воздушного и подводного транспорта (воздушный шар, парашют), архитектуре, технике, искусстве и быту. Центральная симметрия наиболее характерна для плодов растений и некоторых цветов(голубика, черника, вишня, цветок мать-и-мачехи, цветок кувшинки), а также для животных, ведущих подводный образ жизни (амёба).

Примеры из жизни. Одним из самых красивых примеров центральной симметрии является снежинка. Центральную симметрию имеют многие геометрические тела. К ним следует отнести все правильные многогранники (за исключением тетраэдра), все правильные призмы с четным числом боковых граней, некоторые тела вращения (эллипсоид, цилиндр, гиперболоид, тор, шар).

Примеры решения задач. Дано: ABCD - параллелограмм, треугольники ABM, BCK, CDP, DAH - правильные Доказать: KPHM - параллелограмм Решение:

Дано: угол ABC, точка D Дано: угол ABC, точка D Построить отрезок с концами на сторонах данного угла, середина которого находилась бы в точке D Решение: