Презентация на тему: Площадь поверхности призмы

Урок 5 Площадь поверхности призмы

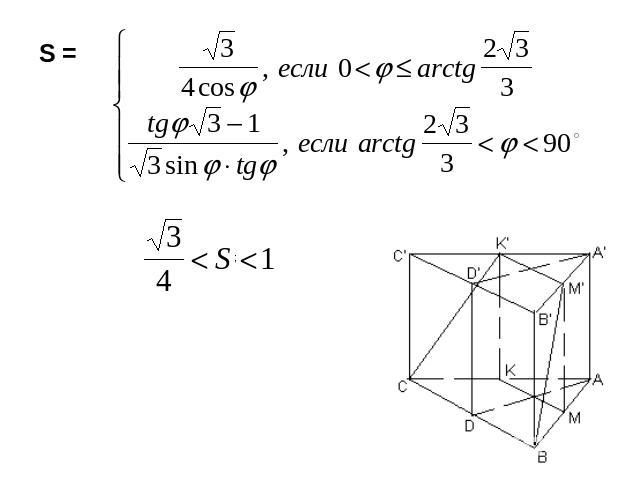
Основанием треугольной призмы является равнобедренный прямоугольный треугольник. Ровно одна ее грань — квадрат, известны длины ее ребер и высота (длины меньшего ребра основания и бокового ребра – b; высоты – H) Как вычислить угол между:
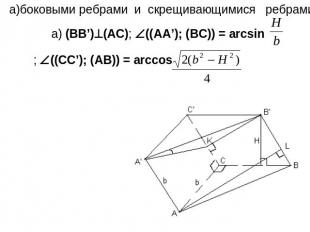
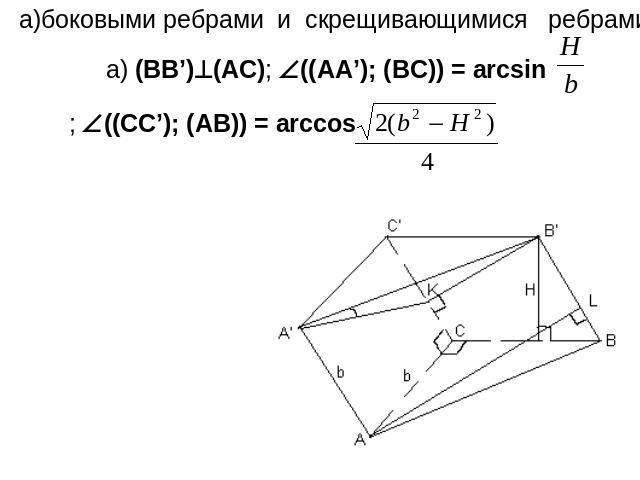
а)боковыми ребрами и скрещивающимися ребрами основания;
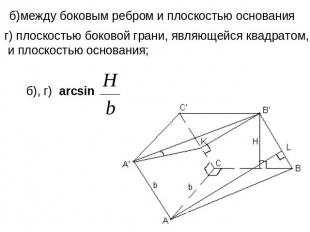
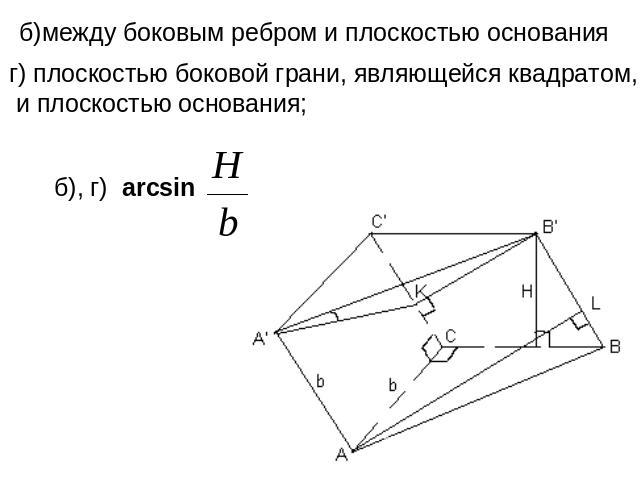
б)между боковым ребром и плоскостью основания г) плоскостью боковой грани, являющейся квадратом, и плоскостью основания;
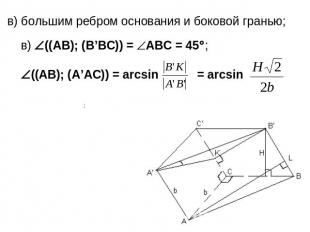
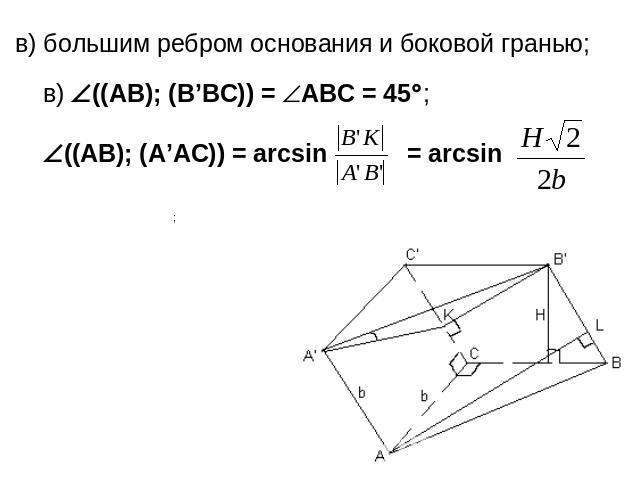
в) большим ребром основания и боковой гранью;
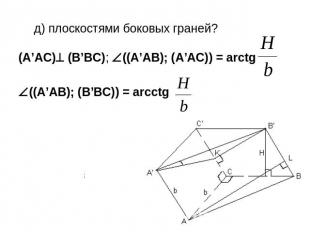
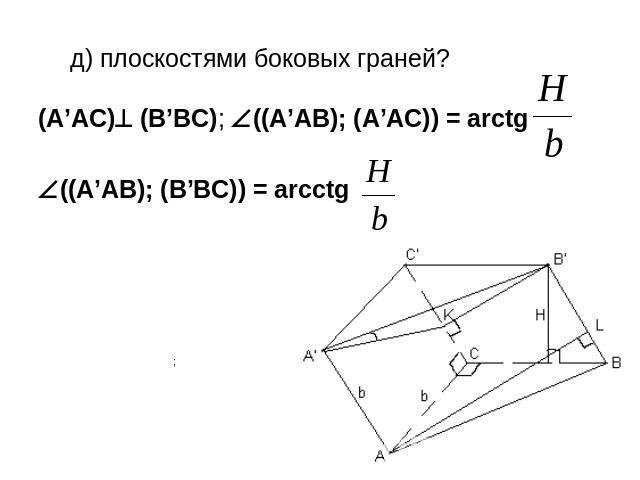
д) плоскостями боковых граней?
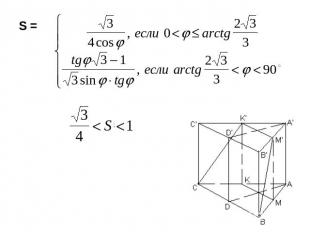
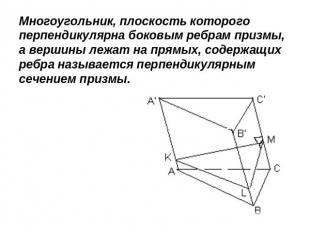
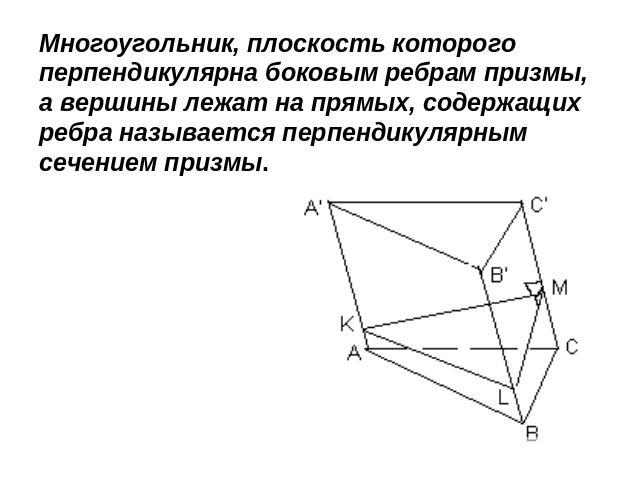
Многоугольник, плоскость которого перпендикулярна боковым ребрам призмы, а вершины лежат на прямых, содержащих ребра называется перпендикулярным сечением призмы.

Как построить перпендикулярное сечение призмы? Является ли оно сечением призмы? Сколько перпендикулярных сечений у любой призмы? Докажите, что они равны. Докажите, что перпендикулярное сечение призмы перпендикулярно каждой ее боковой грани

Докажите, что точки касания вписанного в призму шара с ее боковыми гранями лежат в одном из перпендикулярных сечений призмы В каком случае перпендикулярное сечение призмы равно ее основанию? Как связаны площади перпендикулярного сечения призмы и ее основания?
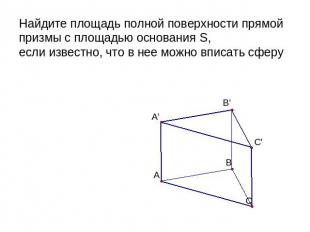
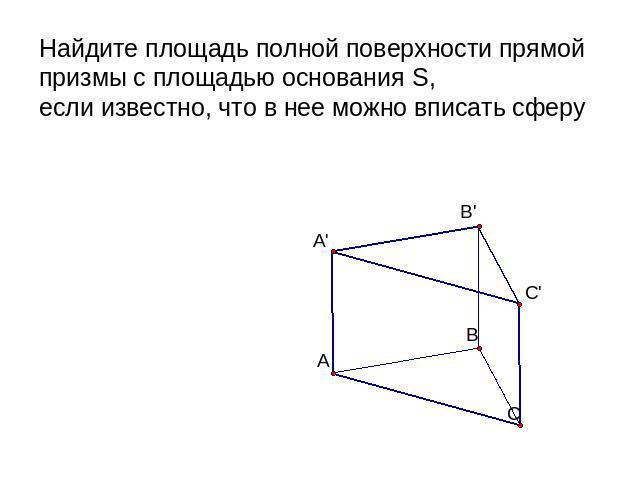
Найдите площадь полной поверхности прямой призмы с площадью основания S, если известно, что в нее можно вписать сферу
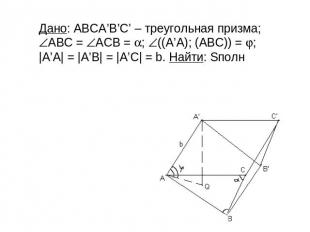
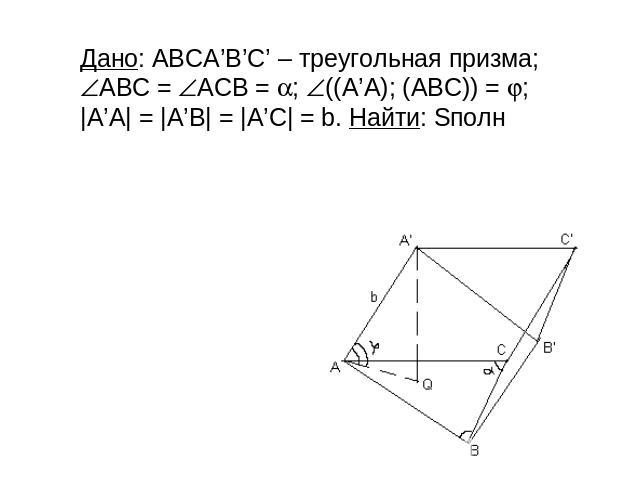
Дано: АВСA’B’C’ – треугольная призма; АВС = АСB = ; ((A’A); (ABC)) = ; |A’A| = |A’B| = |A’C| = b. Найти: Sполн

Уроки 6 Параллелепипед

Сколько граней, являющихся прямоугольниками, может быть в параллелепипеде?

Установите вид параллелепипеда, если: а) все его грани равны; б) все его грани равновелики; в) все его диагонали равны; г) два диагональных сечения перпендикулярны основанию; д) две его смежные грани — квадраты; е) перпендикулярное сечение к каждому ребру является прямоугольником; ж) около него можно описать сферу; з) в него можно вписать сферу. (Диагональное сечение параллелепипеда и, вообще, призмы проходит через параллельные диагонали оснований призмы.)

Докажите, что результат пункта ж) около него можно описать сферу является Н. и Д. условием описания сферы около параллелепипеда
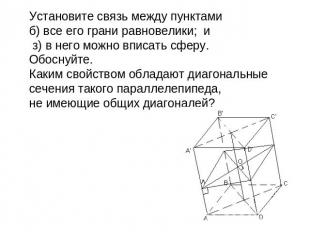
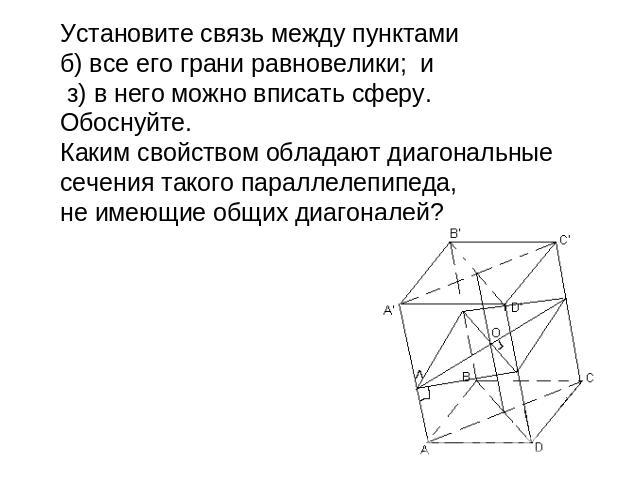
Установите связь между пунктами б) все его грани равновелики; и з) в него можно вписать сферу. Обоснуйте. Каким свойством обладают диагональные сечения такого параллелепипеда, не имеющие общих диагоналей?
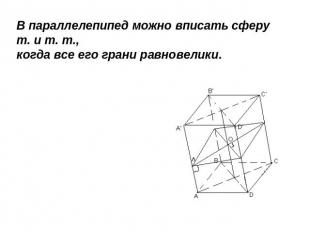
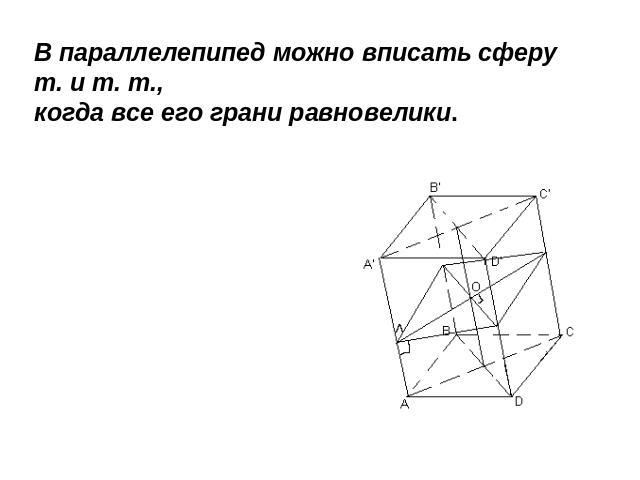
В параллелепипед можно вписать сферу т. и т. т., когда все его грани равновелики.

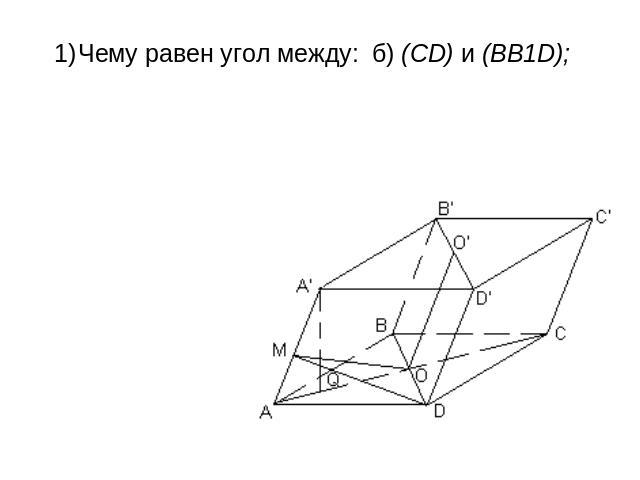
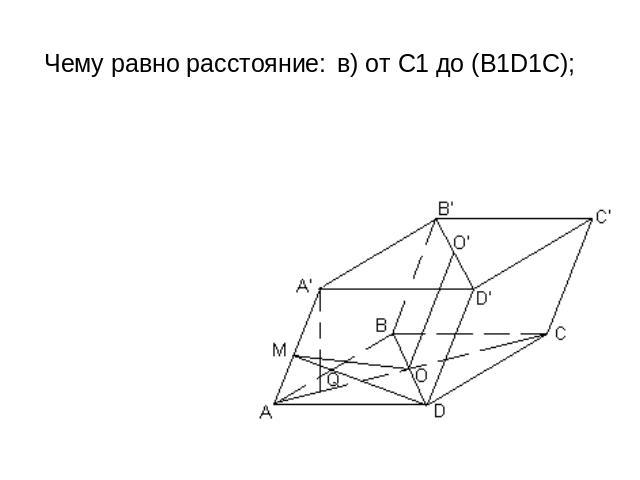
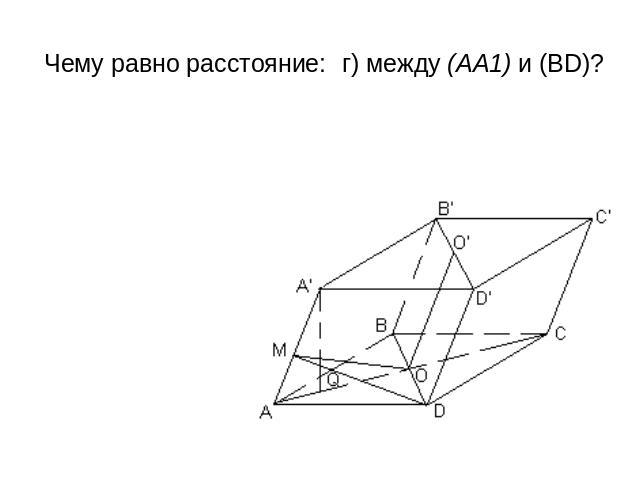
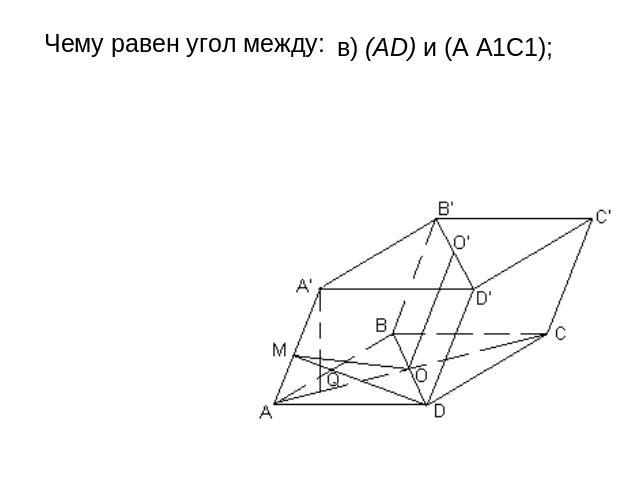
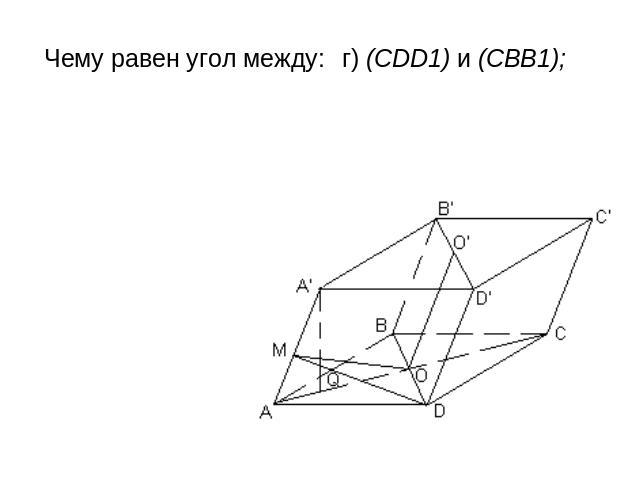
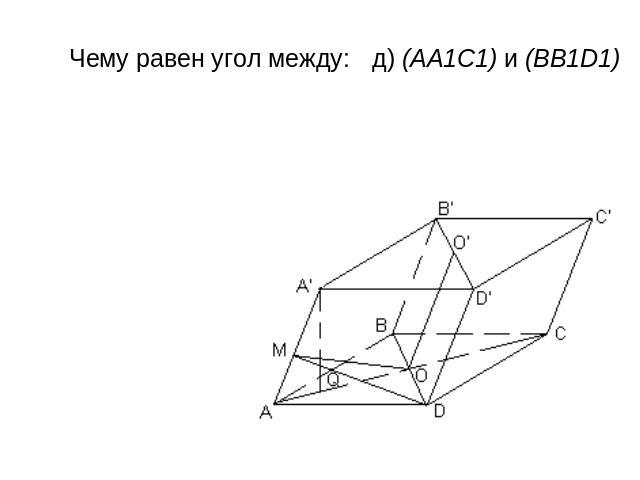
Все грани параллелепипеда АВСDA1В1С1D1 — ромбы.Их равные острые углы сходятся в вершине А. Пусть каждое его ребро равно 1, а острый угол в грани равен 60°. Чему равен угол между: а) боковым ребром и плоскостью основания; б) (CD) и (BB1D); в) (AD) и (А А1С1); г) (CDD1) и (CBB1); д) (АА1С1) и (BB1D1) 2) Чему равно расстояние: а) от A1 до основания; б) от A до (BDD1); в) от С1 до (В1D1С); г) между (AA1) и (BD)?

Все грани параллелепипеда АВСDA1В1С1D1 — ромбы.Их равные острые углы сходятся в вершине А. Пусть каждое его ребро равно 1, а острый угол в грани равен 60°. Чему равен угол между: а) боковым ребром и плоскостью основания;
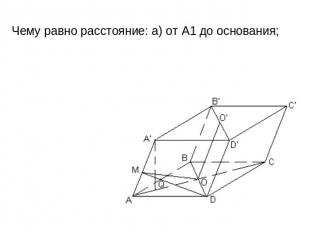
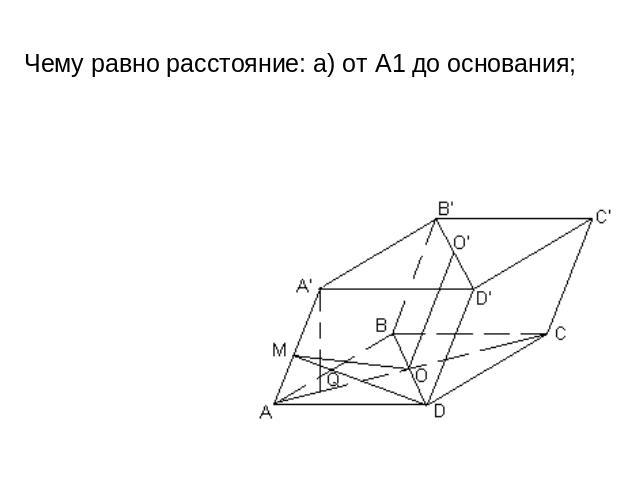
Чему равно расстояние: а) от A1 до основания;
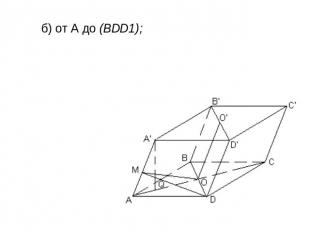
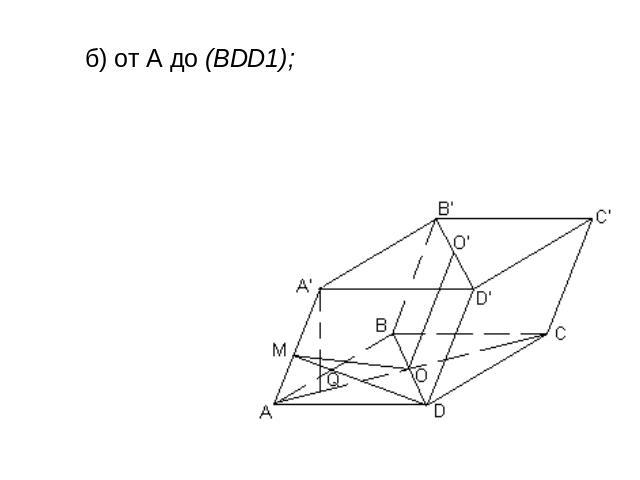
б) от A до (BDD1);
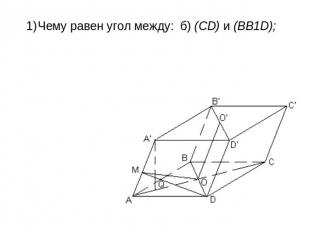
Чему равен угол между:
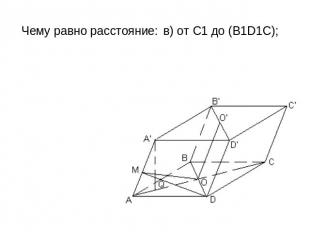
Чему равно расстояние:
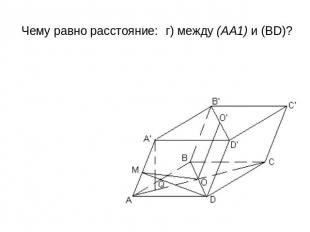
Чему равно расстояние:
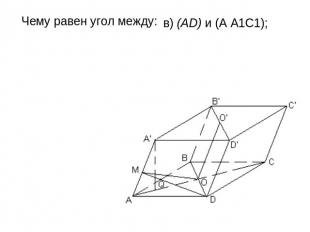
Чему равен угол между:
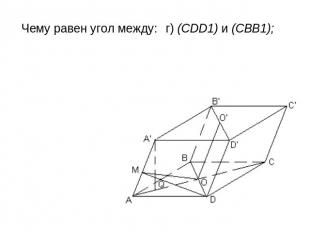
Чему равен угол между:
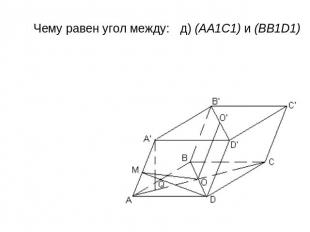
Чему равен угол между: