Презентация на тему: Принцип Кавальери

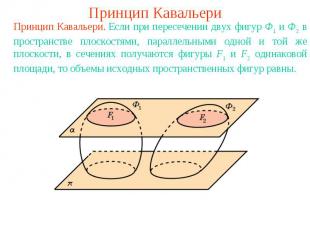
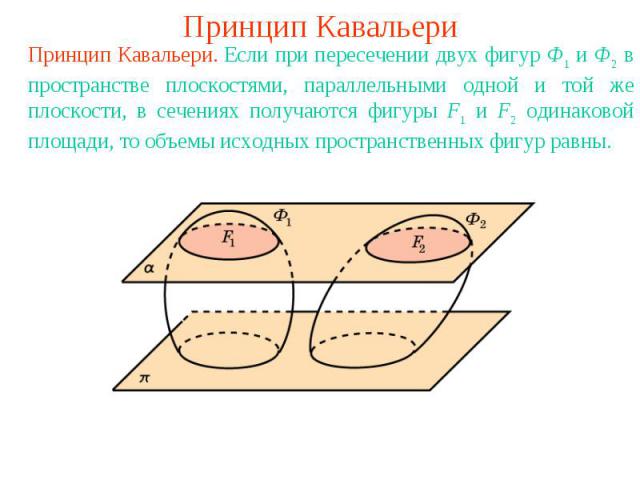
Принцип КавальериПринцип Кавальери. Если при пересечении двух фигур Ф1 и Ф2 в пространстве плоскостями, параллельными одной и той же плоскости, в сечениях получаются фигуры F1 и F2 одинаковой площади, то объемы исходных пространственных фигур равны.

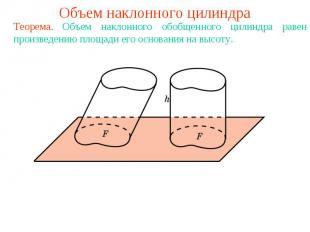
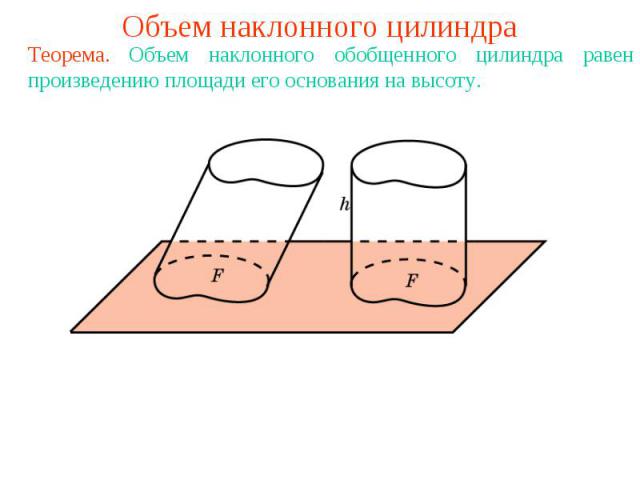
Объем наклонного цилиндраТеорема. Объем наклонного обобщенного цилиндра равен произведению площади его основания на высоту.

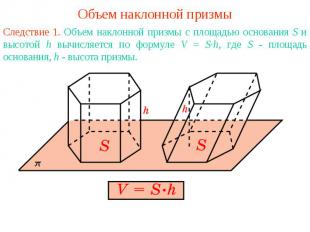
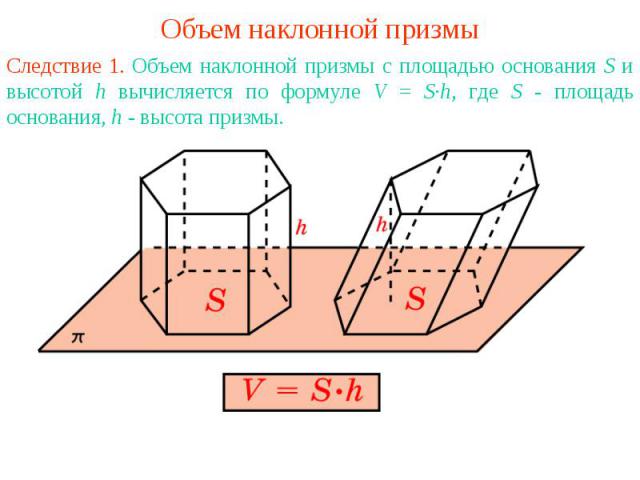
Объем наклонной призмыСледствие 1. Объем наклонной призмы с площадью основания S и высотой h вычисляется по формуле V = S·h, где S - площадь основания, h - высота призмы.

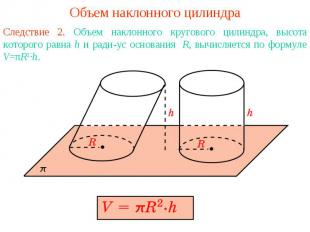
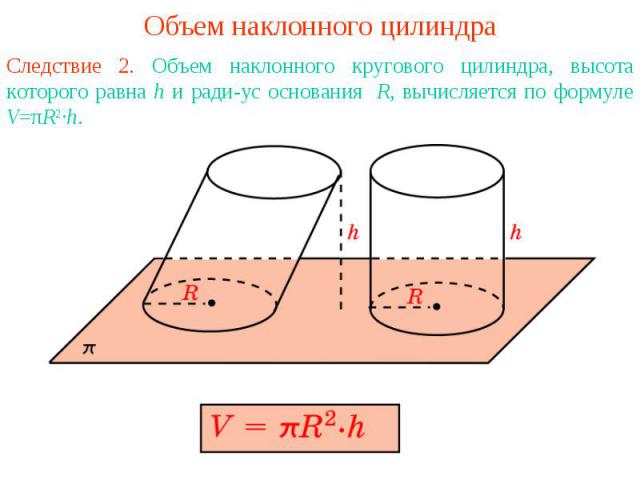
Объем наклонного цилиндраСледствие 2. Объем наклонного кругового цилиндра, высота которого равна h и радиус основания R, вычисляется по формуле V=πR2·h.

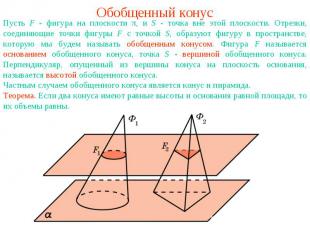
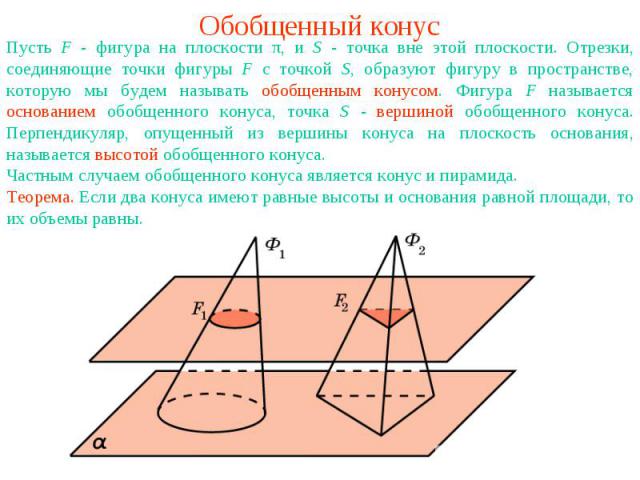
Обобщенный конусПусть F - фигура на плоскости π, и S - точка вне этой плоскости. Отрезки, соединяющие точки фигуры F с точкой S, образуют фигуру в пространстве, которую мы будем называть обобщенным конусом. Фигура F называется основанием обобщенного конуса, точка S - вершиной обобщенного конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой обобщенного конуса.Теорема. Если два конуса имеют равные высоты и основания равной площади, то их объемы равны.

Упражнение 1Верно ли, что две пирамиды, имеющие общее основание и вершины, расположенные в плоскости, параллельной основанию, равновелики?

Упражнение 2Верно ли, что любая плоскость, проходящая через центры оснований наклонного кругового цилиндра, делит его на равновеликие части?

Упражнение 3В основаниях наклонной призмы квадраты. Верно ли, что любая плоскость, проходящая через центры квадратов, делит призму на две равновеликие части?

Упражнение 4Два цилиндра имеют равные высоты, а площадь основания одного в два раза больше площади основания другого. Как относятся их объемы?

Упражнение 5Верно ли, что любая плоскость, проходящая через вершину и центр основания наклонного кругового конуса, делит его на равновеликие части?

Упражнение 6В основании пирамиды квадрат. Верно ли, что любая плоскость, проходящая через вершину пирамиды и центр основания, делит пирамиду на две равновеликие части?

Упражнение 7Два конуса имеют равные высоты, а площадь основания одного в три раза больше площади основания другого. Как относятся их объемы?

Упражнение 8Найдите объем наклонной призмы, площадь основания которой равна S, а боковое ребро b наклонено к плоскости основания под углом φ.

Упражнение 9Стороны основания параллелепипеда равны 6 дм и 8 дм, угол между ними 45°. Боковое ребро равно 7 дм и наклонено к плоскости основания под углом 45°. Найдите объем параллелепипеда.

Упражнение 10Найдите объем наклонного параллелепипеда, у которого площадь основания равна Q, а боковое ребро, равное b, наклонено к плоскости основания под углом φ.

Упражнение 11Найдите объем наклонного кругового цилиндра, радиус основания которого равен R и образующая b наклонена к плоскости основания под углом φ.

Упражнение 12Основанием наклонного параллелепипеда служит квадрат, сторона которого равна 1 м. Одно из боковых ребер образует с каждой прилежащей стороной основания угол в 60° и равно 2 м. Найдите объем параллелепипеда.

Упражнение 13Основанием наклонной призмы является равносторонний треугольник со стороной a. Одна из боковых граней перпендикулярна основанию и является ромбом, у которого меньшая диагональ равна d. Найдите объем призмы.

Упражнение 14Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между ними равны 26 см, 25 см и 17 см. Определите объем призмы.

Упражнение 15Даны три параллелепипеда. Проведите плоскость так, чтобы она разделила каждый параллелепипед на две части равного объема.Ответ: Плоскость, проходящая через центры симметрии параллелепипедов.