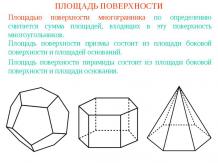
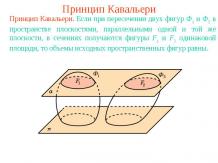
Презентация на тему: Аналитическое задание многогранников

Аналитическое задание многогранников Неравенства ax + by + cz + d 0 и ax + by + cz + d 0 определяют полупространства, на которые плоскость, заданная уравнением ax + by + cz + d = 0, разбивает пространство. Если грани выпуклого многогранника лежат в плоскостях, задаваемых уравнениями

Упражнение 1 Два полупространства задаются неравенствамиa1x + b1y + c1z + d1 0, a2x + b2y + c2z + d2 0. Как будет задаваться пересечение этих полупространств?

Упражнение 2 Определите, какому полупространству 5x + 3y - z - 2 0 или 5x + 3y - z - 2 0 принадлежит точка: а) А(1,0,0); б) B(0,1,0); в) C(0,0,1).

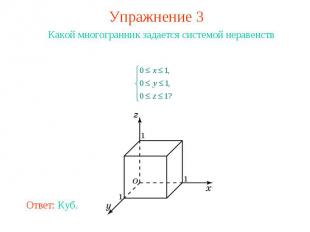
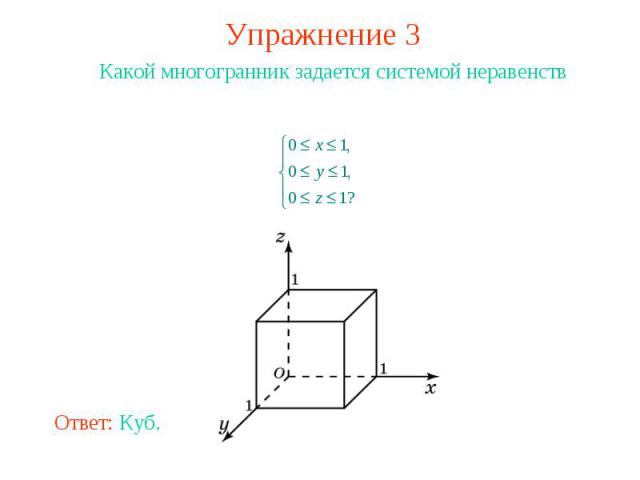
Упражнение 3 Какой многогранник задается системой неравенств

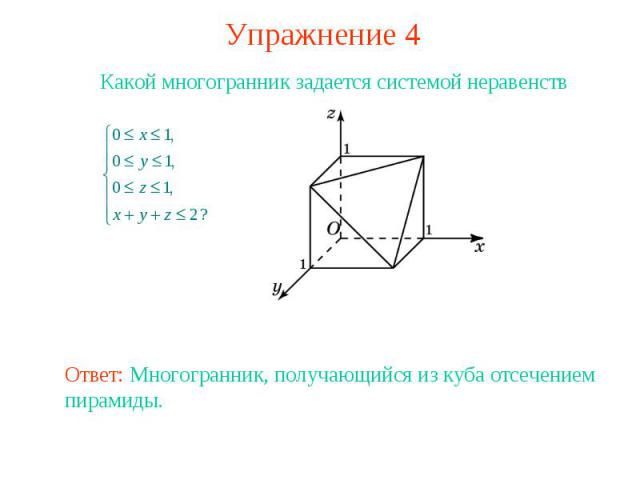
Упражнение 4 Какой многогранник задается системой неравенствОтвет: Многогранник, получающийся из куба отсечением пирамиды.

Упражнение 5 Какую фигуру в пространстве задает следующая система неравенствОтвет: Прямоугольный параллелепипед.

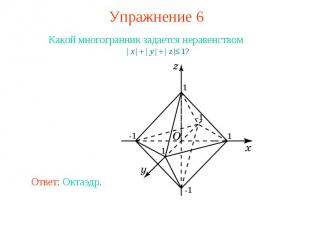
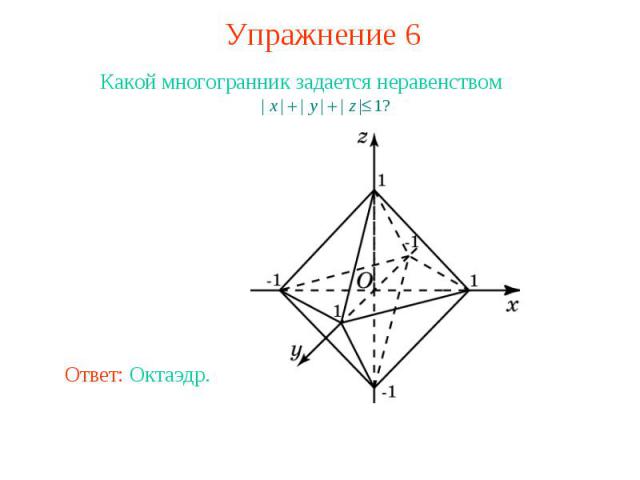
Упражнение 6 Какой многогранник задается неравенством

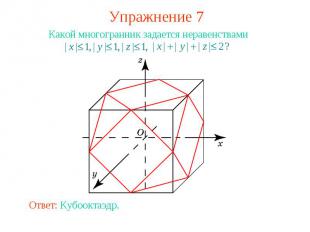
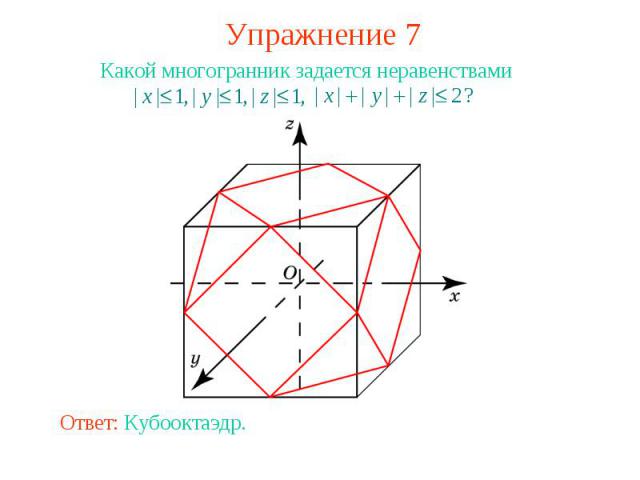
Упражнение 7 Какой многогранник задается неравенствами

Упражнение 8 Найдите неравенства, задающие правильный тетраэдр, вершины которого имеют координаты: (1,1,-1), (1,-1,1), (-1,1,1), (-1,-1,-1).

Упражнение 9 Какая фигура в пространстве задается системой неравенств?

Упражнение 10 Напишите неравенства, определяющие конус с вершиной в точке S(0,0,h) и основание которого - круг радиуса R, лежащий в плоскости Oxy.

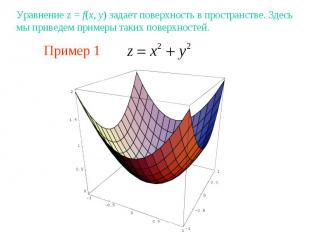
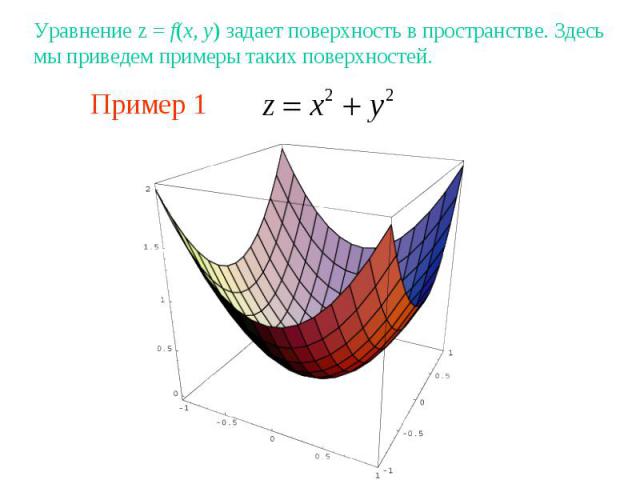
Пример 1Уравнение z = f(x, y) задает поверхность в пространстве. Здесь мы приведем примеры таких поверхностей.

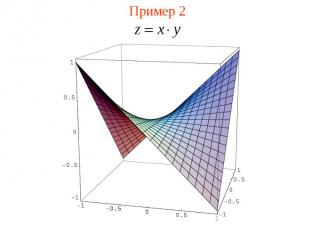
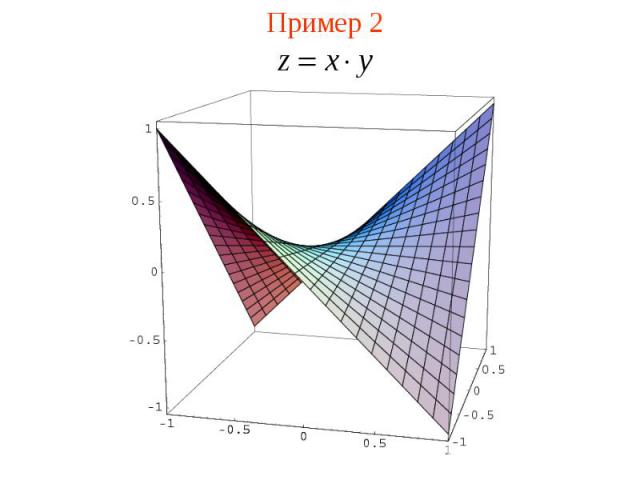
Пример 2

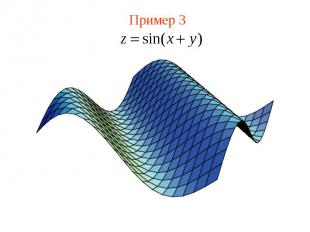
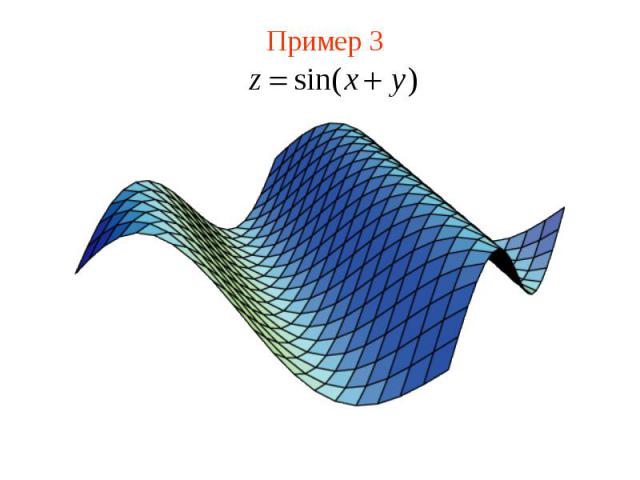
Пример 3

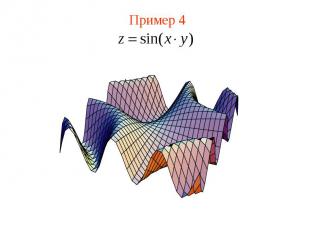
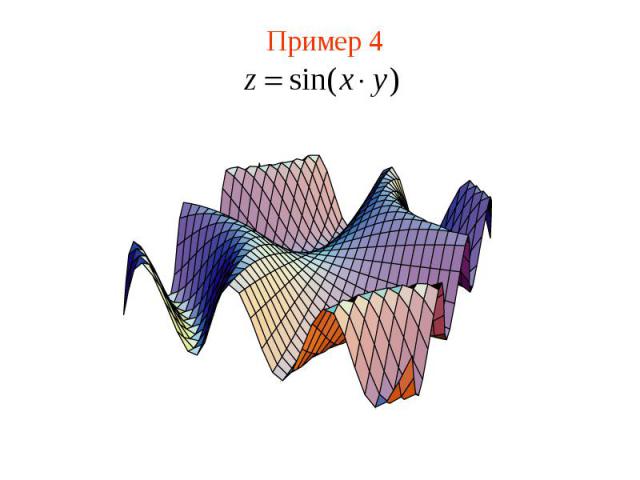
Пример 4

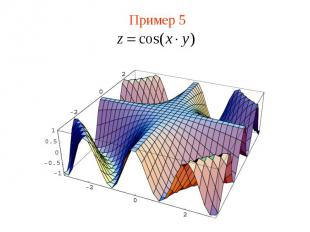
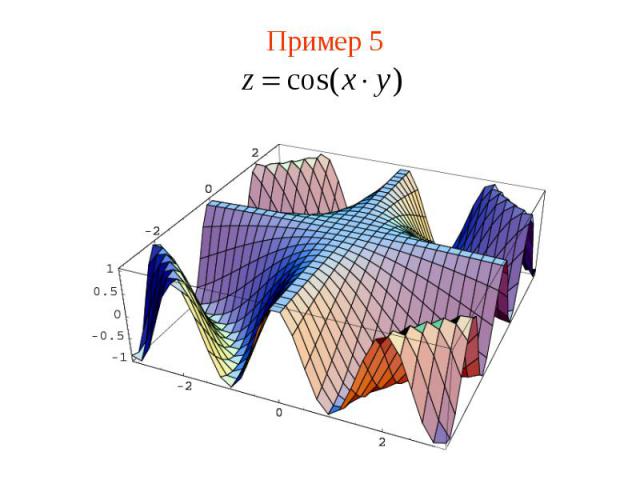
Пример 5

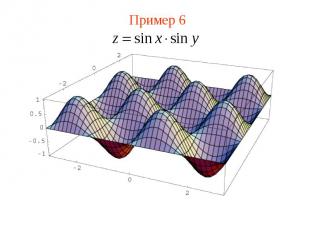
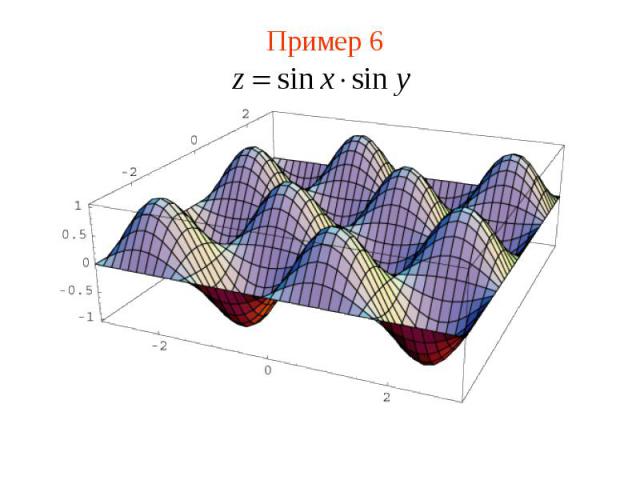
Пример 6

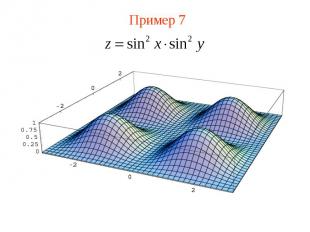
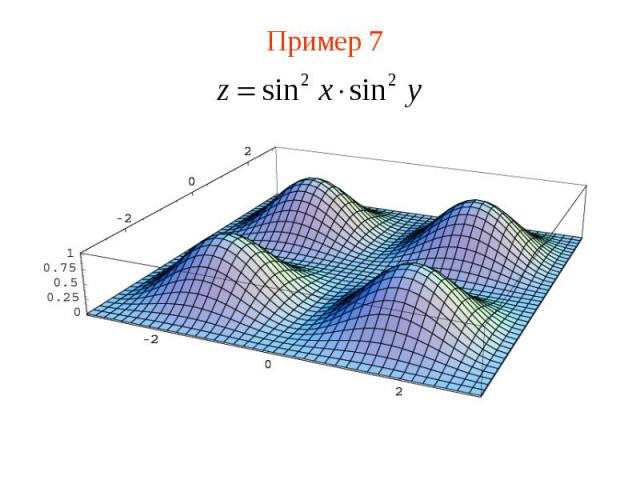
Пример 7

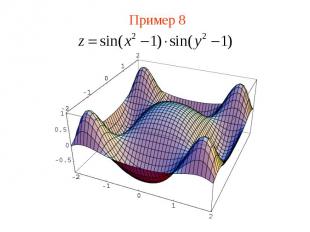
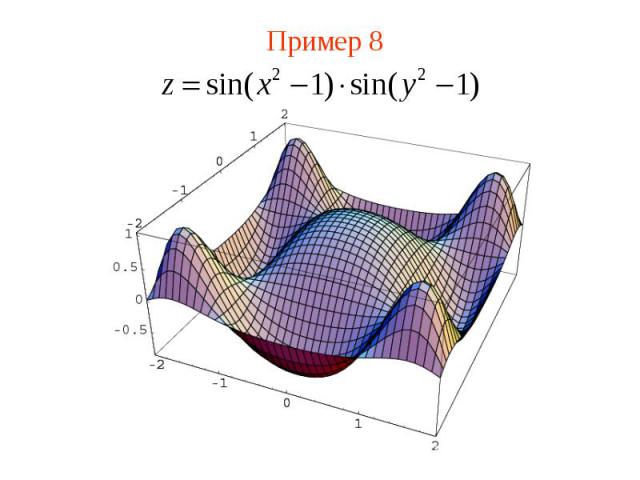
Пример 8