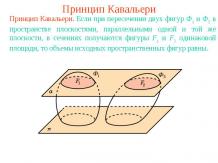
Презентация на тему: Расстояние между точками

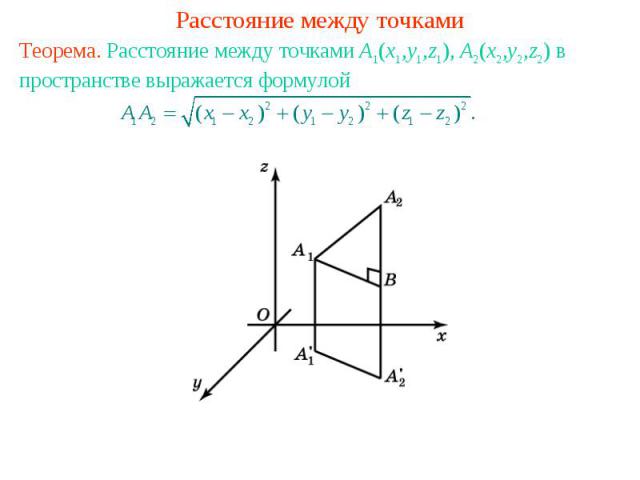
Расстояние между точкамиТеорема. Расстояние между точками A1(x1,y1,z1), A2(x2,y2,z2) в пространстве выражается формулой

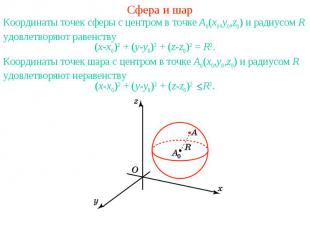
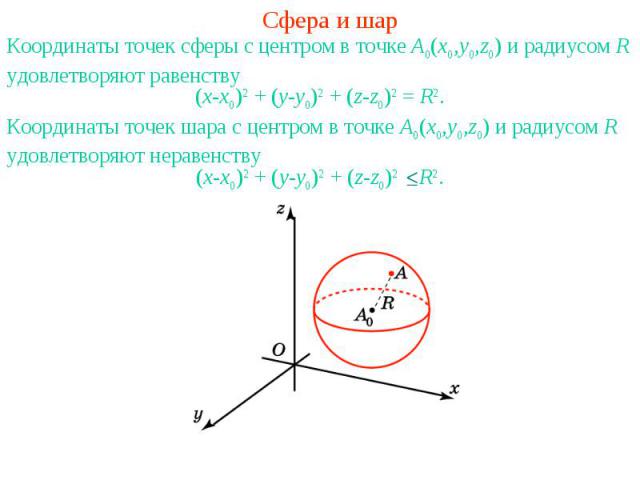
Сфера и шарКоординаты точек сферы с центром в точке A0(x0,y0,z0) и радиусом R удовлетворяют равенствуКоординаты точек шара с центром в точке A0(x0,y0,z0) и радиусом R удовлетворяют неравенству

Упражнение 1Найдите расстояние между точками A1(1, 2, 3) и A2(-1, 1, 1), B1(3, 4, 0) и B2(3, -1, 2).

Упражнение 2Какая из точек A (2, 1, 5) или B (-2, 1, 6) лежит ближе к началу координат?

Упражнение 3Даны точки M (1,-2,-3), N (-2,3,1) и K (3,1,-2). Найдите периметр треугольника MNK.

Упражнение 4Определите вид треугольника, если его вершины имеют координаты: A(0, 0, 2), B(0, 2, 0), C(2, 0, 0).

Упражнение 5Найдите координаты центра C и радиус R сферы, заданной уравнением:а) (x - 2)2 + (y + 5)2 + z2 = 9;б) x2 + (y - 6)2 + (z + 1)2 = 11.

Упражнение 6Напишите уравнение сферы: а) с центром в точке O(0, 0, 0) и радиусом 1; б) с центром в точке C (1, -2, 3) и радиусом 4.

Упражнение 7Напишите уравнение сферы с центром в точке O(1, 2, -1), касающейся координатной плоскости: а) Oxy; б) Oxz; в) Oyz.

Упражнение 8Напишите уравнение сферы с центром в точке O(3, -2, 1), касающейся координатной прямой: а) Ox; б) Oy; в) Oz.

Упражнение 9Найдите уравнения сфер радиуса R, касающихся трех координатных плоскостей.

Упражнение 10Докажите, что уравнение x2 - 4x + y2 + z2=0 задает сферу в пространстве. Найдите ее радиус и координаты центра.

Упражнение 11Как расположена точка А(5, 1, 2) относительно сферы x2 + y2 + z2 - 8x + 4y +2z - 4 = 0?

Упражнение 12Как расположены друг относительно друга сферы (x - 1)2 + (y - 2)2 + (z + 1)2 = 1, (x - 2)2 + (y - 1)2 + (z - 1)2 = 1?

Упражнение 13Координаты точек какой фигуры удовлетворяют неравенству: а) (x-x0)2+(y-y0)2+(z-z0)2R2?

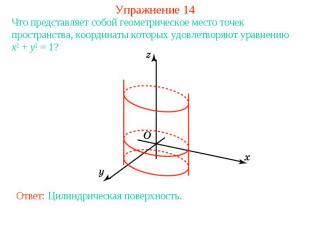
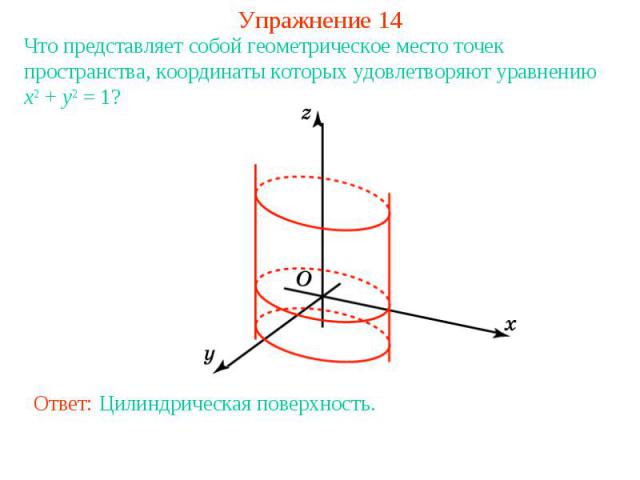
Упражнение 14Что представляет собой геометрическое место точек пространства, координаты которых удовлетворяют уравнению x2 + y2 = 1?