Презентация на тему: Построение сечений многогранников

Построение сечений многогранниковПрезентация выполненаучителем математики МОУ лицея № 28 имени Н.А.Рябова г.ТамбоваБеляевой О.П.

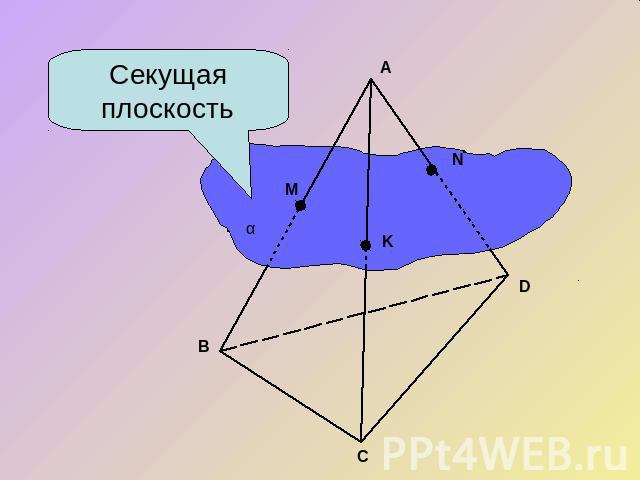
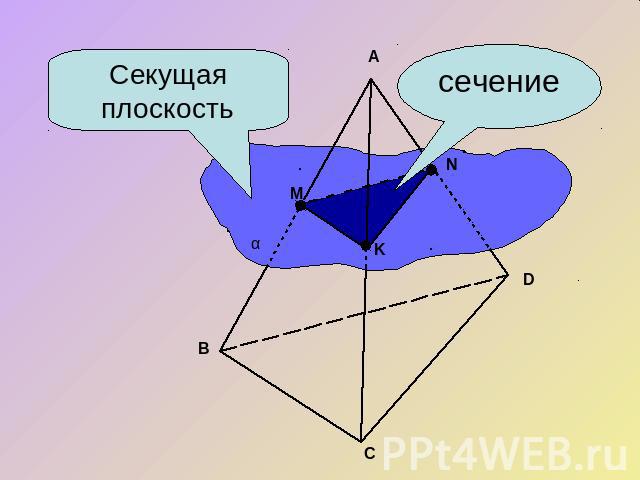
Определение сечения.Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Секущая плоскость

Секущая плоскостьсечение

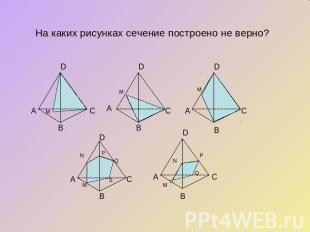
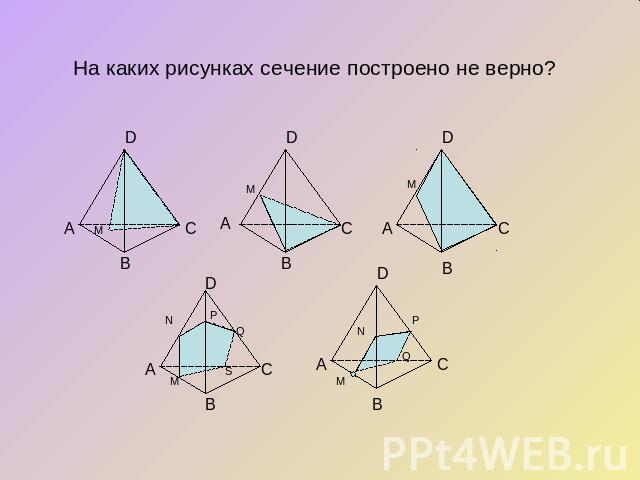
На каких рисунках сечение построено не верно?

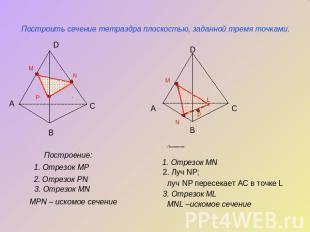
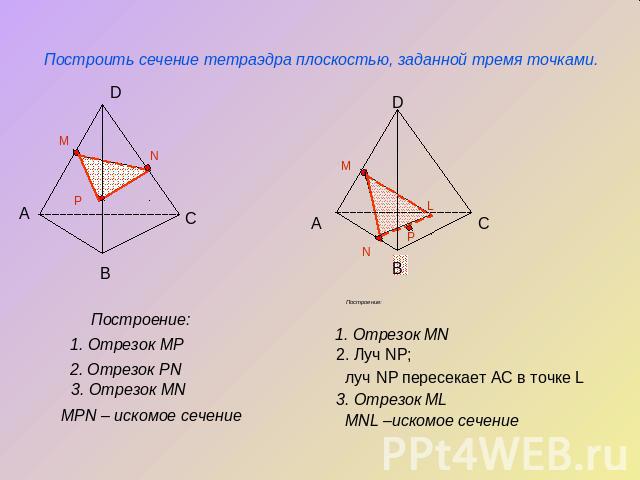
Построить сечение тетраэдра плоскостью, заданной тремя точками.Построение:Отрезок MP Отрезок PNОтрезок MNMPN – искомое сечениеПостроение: Отрезок MN Луч NP; луч NP пересекает АС в точке LОтрезок ML MNL –искомое сечение

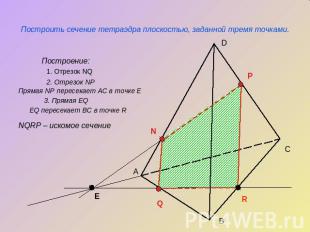
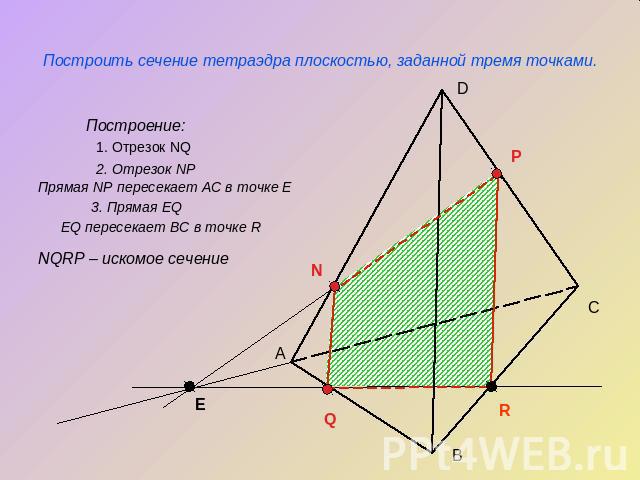
Построить сечение тетраэдра плоскостью, заданной тремя точками.

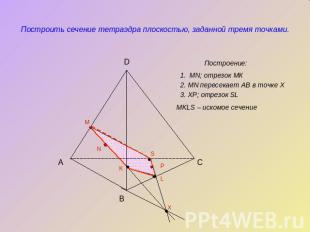
Построить сечение тетраэдра плоскостью, заданной тремя точками.

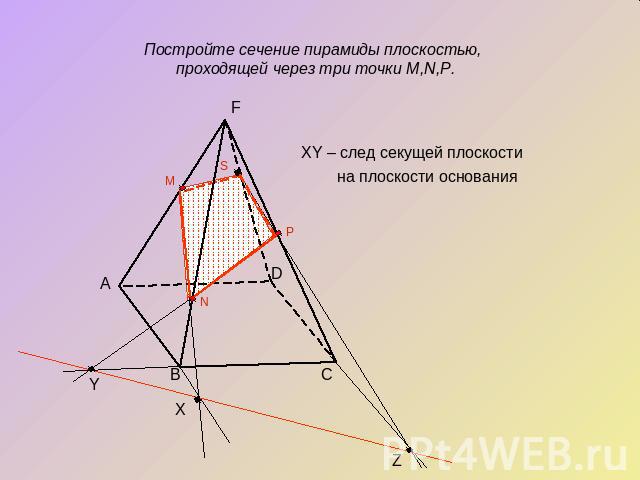
Аксиоматический методСуть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .    

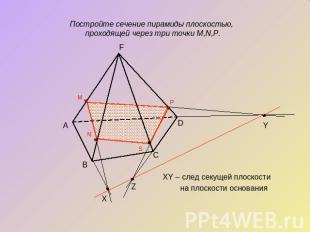
Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.XY – след секущей плоскости на плоскости основания

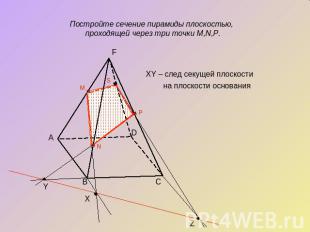
Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.XY – след секущей плоскости на плоскости основания

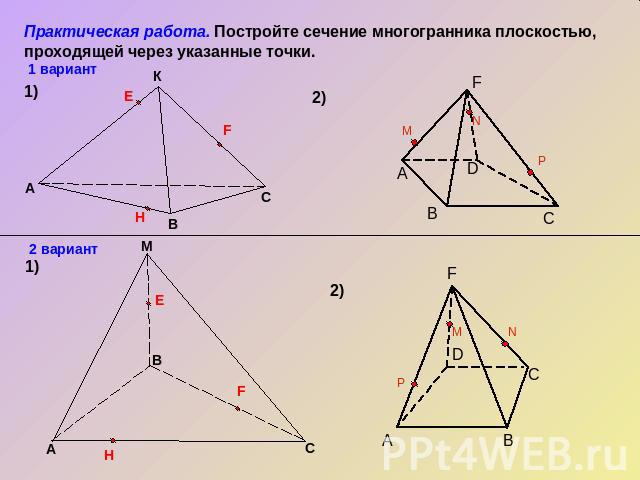
Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.

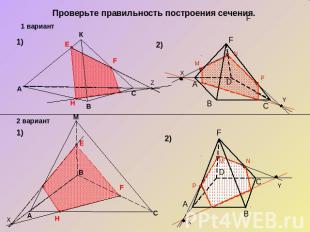
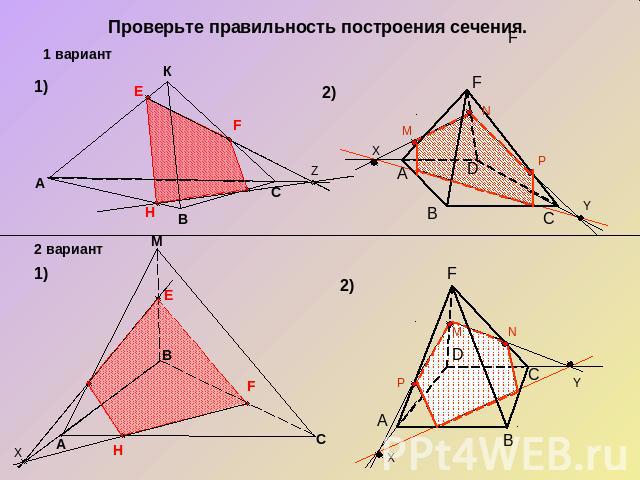
Проверьте правильность построения сечения.

Домашнее задание:4. п.14. учебника2. № 72, №73, № 74, №75.