Презентация на тему: Построение сечений многогранников

Построение сечениймногогранников

Содержание Понятие сеченияПодготовительные задачиОсновные способы построения сечения Возможные ошибкиВиды сечений тел вращенияЗадания на построение сечений

Понятие сечения Для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно уметь строить на рисунке их сечения различными плоскостями. Назовем секущей плоскостью тетраэдра (параллелепипеда) любую плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда). Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, сторонами которого является эти отрезки, называется сечением тетраэдра (параллелепипеда).

Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

Подготовительные задачи Задача 1. Дан тетраэдр DABC, точка К лежит на ребре DB, точка М – на ребре DC. Найти точку пересечения прямой с плоскостью основания. Решение.Соединим точки М и К, продолжимпрямую МК. Продолжим одну из прямых плоскости АВС – прямую ВС. Точка Е – точка пересечения прямой МК и плоскости АВС.

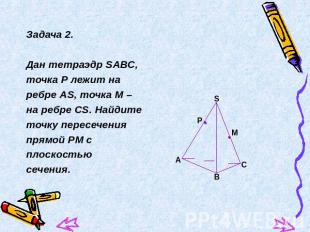
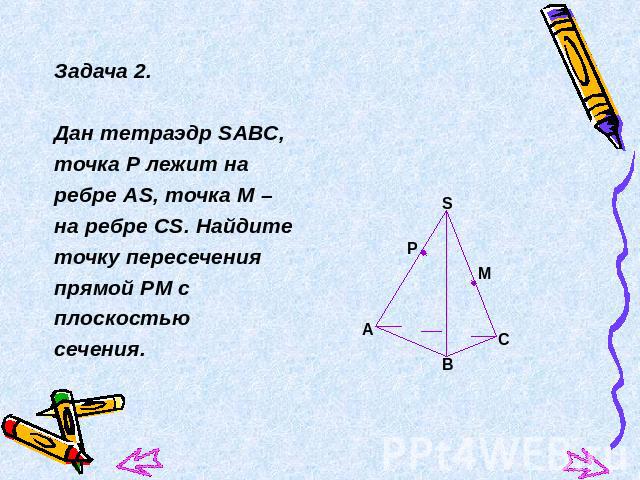
Задача 2.Дан тетраэдр SАВС, точка Р лежит наребре АS, точка М – на ребре СS. Найдитеточку пересеченияпрямой РМ сплоскостью сечения.

Задача 3. Дан параллелепипед АВСDА1В1С1D1. Точка Р лежит на ребре ВС, точка К – на ребре АD, точка М на ребре СС1. Найдите точки пересечения прямой РК с плоскостью DD1С, прямой РМ с плоскостью А1В1С1.

Виды сечений тел вращенияКонусЦилиндрШарСодержание

Конус Рассмотрим сечение конуса различными плоскостями.Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.

Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг (рис. 1).Если секущая плоскость располагается под некоторым углом к оси конуса, то сечение конуса – овал (рис. 2).

Цилиндр Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие цилиндра, а две другие – диаметры оснований. Такое сечение называется осевым.

Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. Такая секущая плоскость отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть данное сечение.

Если секущая плоскость располагается под некоторым углом к оси цилиндра, то сечение цилиндра – овал.

Шар Если расстояние от центра шара до плоскости меньше радиуса шара, то сечение шара плоскостью есть круг.

Основные способы построения сеченийПараллелепипедТетраэдр

Параллелепипед Если данные точки лежат на ребрах, выходящих из одной вершины, нужно: Провести отрезок АВПровести отрезок ВСПровести отрезок АС Треугольник АВС – искомое сечение

Если три данные точки лежат на ребрах, выходящих не из одной точки, то нужно:провести отрезки АВ и ВСчерез точку А провести прямую, параллельную ВСчерез точку С – прямую, параллельную АВобозначить буквами Е и D – точки пересечения этих прямых с ребрами нижней гранипровести отрезок ЕD Пятиугольник АВСDЕ – искомое сечение

Если данные точки А,В и С расположены так, как показано на рисунке, то следует:провести прямую АВ и продолжить нижнее ребро до пересечения его с этой прямой в точке Мчерез точку М провести прямую, параллельную прямой ВС эта прямая пересекается с ребрами нижнего основания в точках Е и Fчерез точку Е провести прямую, параллельную прямой АВ, получим точку Dпровести отрезки АF и СD Шестиугольник АВDСЕF – искомое сечение

Тетраэдр Если точка лежит на боковой грани тетраэдра, то для построения сечения,проходящего через эту точку и параллельного основанию, нужно:провести через точку М прямую, параллельную отрезку АВобозначить буквами Р и Q точки пересечения этой прямой с боковыми ребрами DА и DВ через точку Р провести прямую, параллельную отрезку АСобозначить буквой R точку пересечения этой прямой с ребром DСпровести отрезок QR Треугольник РQR – искомое сечение

Если данные точки (М, N и Р) лежат на ребрах тетраэдра, то следует:Провести отрезки NР и NМПродолжить отрезки NР и ВС до пересечения в точке ЕПровести отрезок ЕМ и продолжить его до пересечения с отрезком АС – точка QПровести отрезок РQ Четырехугольник МNРQ – искомое сечение

Задания на построение сеченийС1. Задача 1Построить в треугольной призме АВСА1В1С1 сечение, проходящее через АВ и середину А1С1.

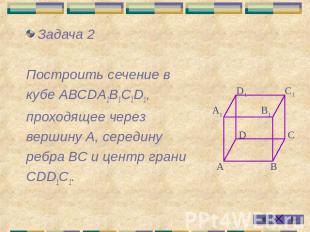
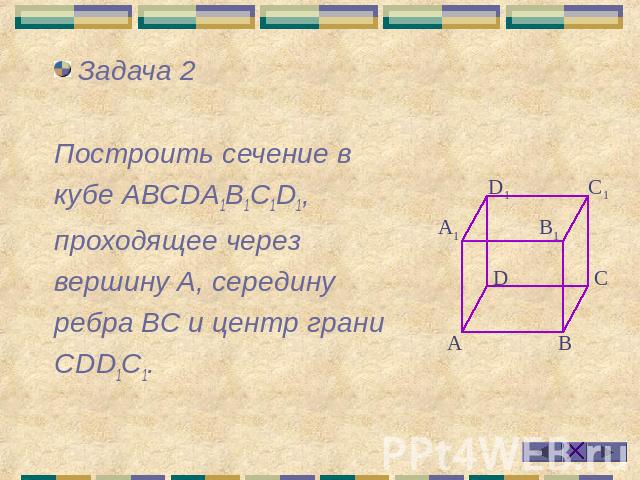
Задача 2Построить сечение в кубе АВСDА1В1С1D1, проходящее через вершину А, середину ребра ВС и центр грани СDD1С1.

Задача 2Построить сечение в кубе АВСDА1В1С1D1, проходящее через вершину А, середину ребра ВС и центр грани СDD1С1.

Возможные ошибкиНаиболее частодопускают следующие ошибки:соединяют точки, лежащие в разных плоскостях (можно провести отрезки АС и СВ, но не АВ)

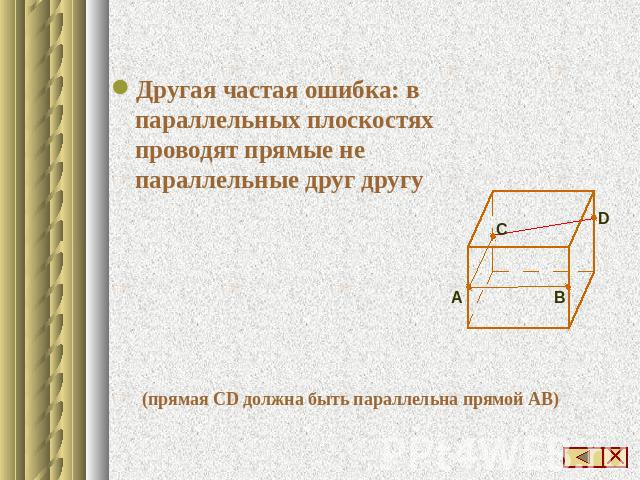
Другая частая ошибка: в параллельных плоскостях проводят прямые не параллельные друг другу (прямая СD должна быть параллельна прямой АВ)

Спасибо за внимание!