Презентация на тему: Решение треугольника
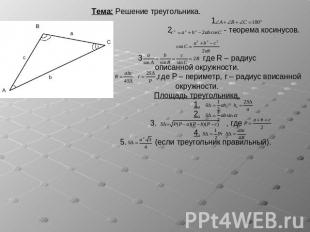
Тема: Решение треугольника. 1 2 - теорема косинусов. 3 где R – радиус описанной окружности. ,где P – периметр, r – радиус вписанной окружности.Площадь треугольника.1.2.3. , где 4.5. (если треугольник правильный).
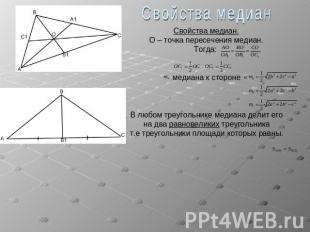
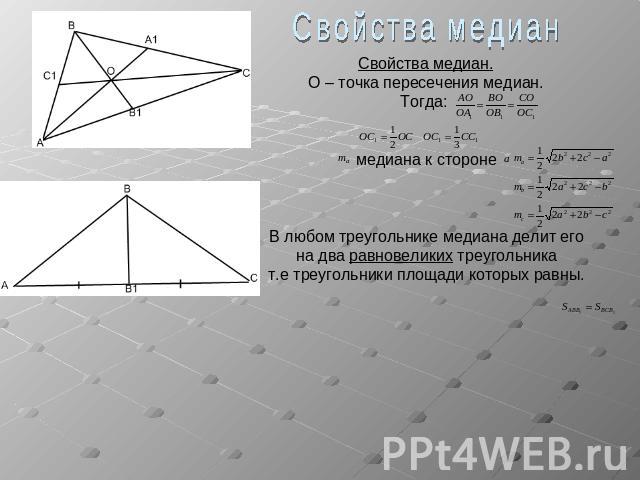
Свойства медианСвойства медиан.О – точка пересечения медиан.Тогда: медиана к стороне В любом треугольнике медиана делит егона два равновеликих треугольникат.е треугольники площади которых равны.
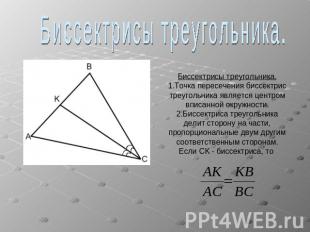
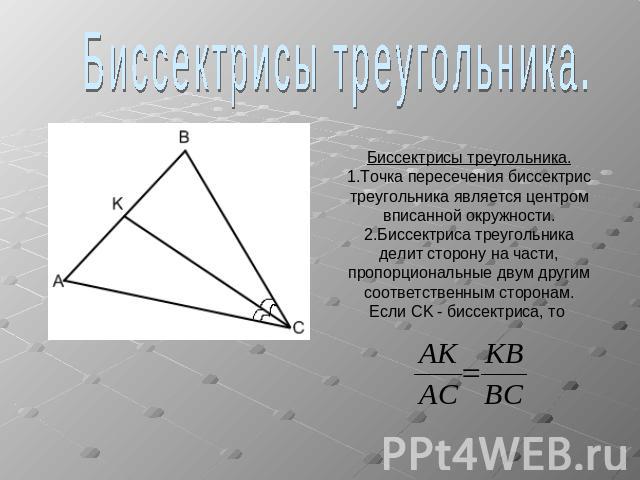
Биссектрисы треугольника.Биссектрисы треугольника.1.Точка пересечения биссектрис треугольника является центром вписанной окружности.2.Биссектриса треугольникаделит сторону на части,пропорциональные двум другимсоответственным сторонам.Если CK - биссектриса, то

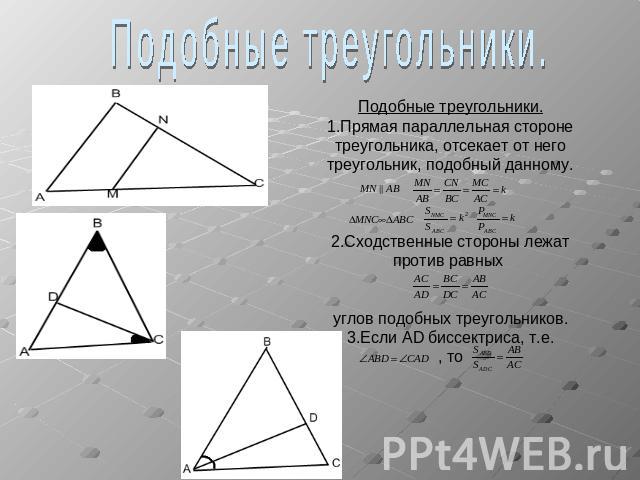
Подобные треугольники.Подобные треугольники.1.Прямая параллельная стороне треугольника, отсекает от него треугольник, подобный данному.2.Сходственные стороны лежат против равных углов подобных треугольников.3.Если AD биссектриса, т.е., то

Задачи!Задача 1.Основание равнобедренного треугольникаравно30 см, а высота, проведённая из вершины основания 24 см. Найти S треугольника.Решение: 1.2. прямоугольный, т.к. BK – высота и медиана равнобедренного треугольника, то 3. как прямоугольные с общим острым углом Тогда:4. Ответ.

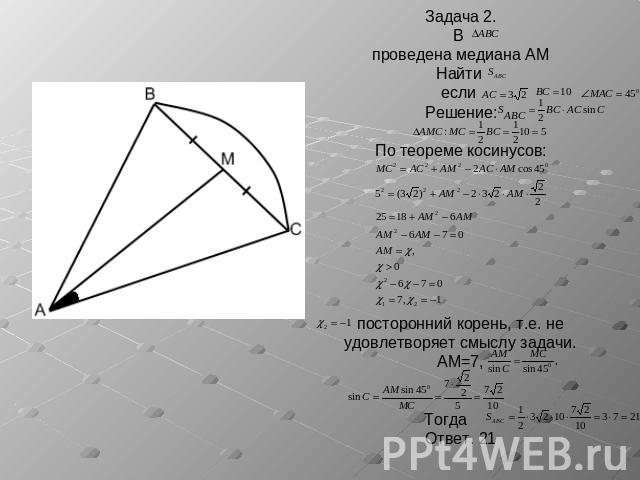
Задача 2.В проведена медиана AMНайти если Решение: По теореме косинусов:посторонний корень, т.е. не удовлетворяет смыслу задачи.AM=7, Тогда Ответ. 21

Задача 3.Найти площадь треугольника, если , а медианаРешение: BM – медиана, значит AM=MC=10.Медиана делит на два равнобедренных треугольникаЗначитТогдаОтвет. 96

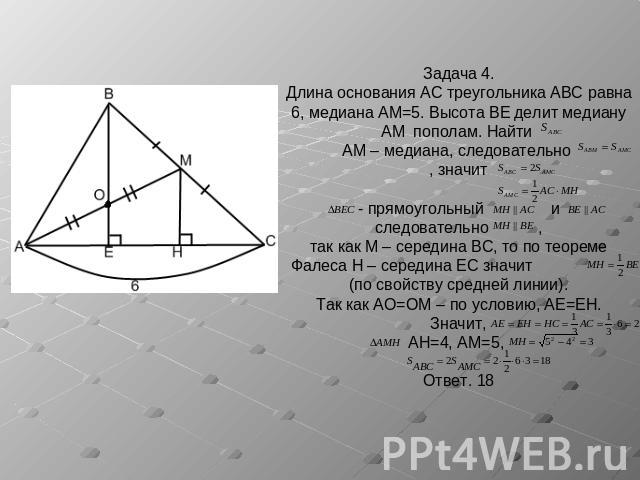
Задача 4.Длина основания AC треугольника ABC равна 6, медиана AM=5. Высота BE делит медиану AM пополам. Найти AM – медиана, следовательно , значит- прямоугольный иследовательно ,так как M – середина BC, то по теореме Фалеса H – середина EC значит (по свойству средней линии).Так как AO=OM – по условию, AE=EH.Значит,AH=4, AM=5, Ответ. 18

СамостоятельноРешить самостоятельно:1.В треугольнике ABC проведена медиана AM.Найти: еслиОтвет. 212.В треугольнике ABC проведена биссектриса BK, длина которой равна 4, причёмНайтиОтвет. 43.В равнобедренном треугольнике ABC (AB=BC) проведена биссектриса AD. Найти AC.Ответ. AC=4.4.Точка M лежит на стороне AO треугольника AOM,Найти.Ответ. 85.В треугольнике ABC AB=BC=15, CA=24.Найти расстояние между точкой пересечения серединных перпендикуляров и точкой пересечения медиан треугольника.Ответ. 44