Презентация на тему: Решение прямоугольного треугольника

Решение прямоугольного треугольника

1)∟А + ∟В = 900 , sinA = cosB2)с2 = а2 + в2 3)а = с cosβ в = с sinβtgB = в/аО – середина АВ ( О – центр описанной окружности)R- радиус описанной окружности,АВ- диаметр описанной окружности.r- радиус вписанной окружности

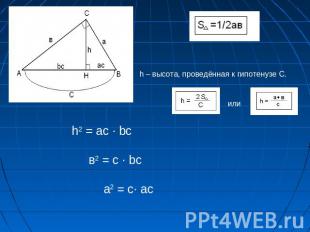
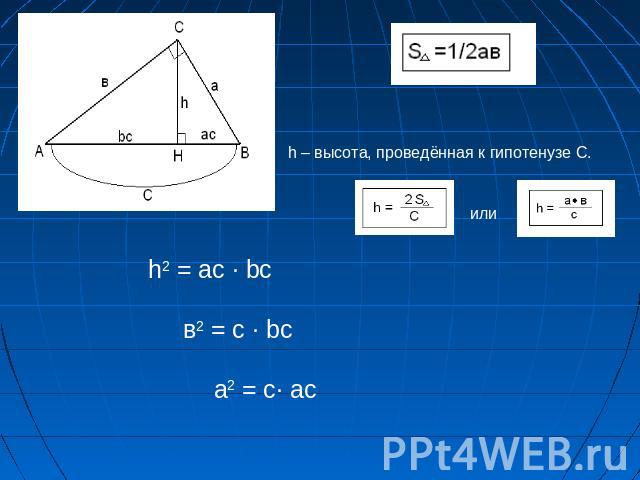
h – высота, проведённая к гипотенузе С.h2 = ac ∙ bc в2 = c ∙ bc a2 = c∙ ac

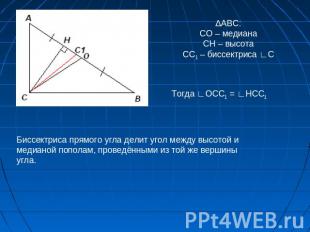
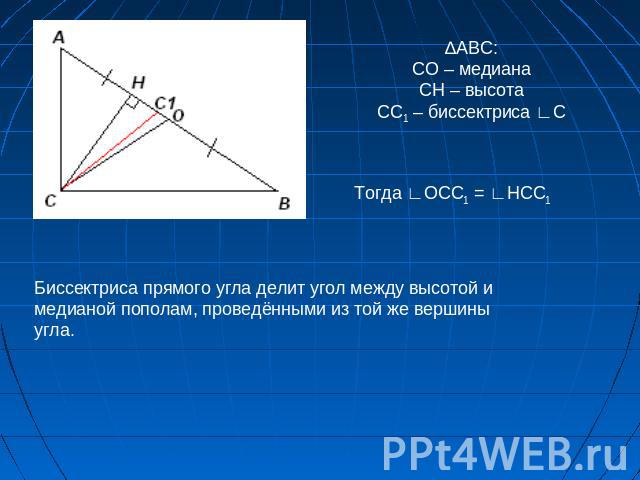
∆АВС:СО – медианаСH – высотаСС1 – биссектриса ∟СТогда ∟ОСС1 = ∟HCC1Биссектриса прямого угла делит угол между высотой и медианой пополам, проведёнными из той же вершины угла.

Примеры решения задачДано: ∆АВС – прямоугольный ( ∟С = 900 ), CH – высота АС = 10, АH = 8Найти: S∆АВСРешение:

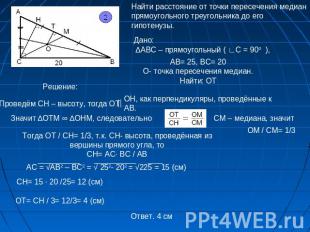
Найти расстояние от точки пересечения медиан прямоугольного треугольника до его гипотенузы.Дано: ∆АВС – прямоугольный ( ∟С = 900 ), АВ= 25, ВС= 20О- точка пересечения медиан.Найти: OTТогда ОТ / CH= 1/3, т.к. CH- высота, проведённая из вершины прямого угла, тоCH= AC∙ BC / AB

Периметр прямоугольного треугольника равен 72см, а радиус вписанной окружности равен 6см. Найти диаметр описанной окружности.АВ- диаметр описанной окружности. О - центр вписанной окружности ( точка пересечения биссектрис углов). (72 –с –с)/ 2= 6,72 -2c = 12,2c= 60,C=30, AB= 30.

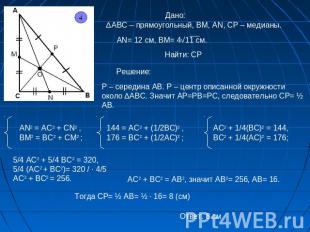
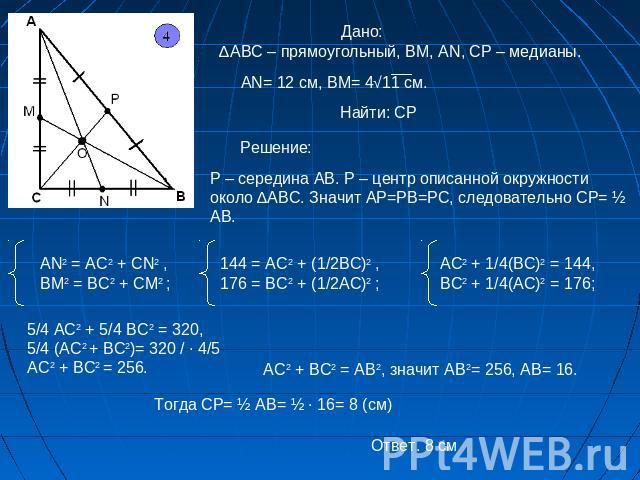
Дано: ∆АВС – прямоугольный, ВМ, АN, CP – медианы. Решение:Р – середина АВ. Р – центр описанной окружности около ∆АВС. Значит АР=РВ=РС, следовательно СР= ½ AB. 5/4 AC2 + 5/4 BC2 = 320,5/4 (AC2 + BC2)= 320 / ∙ 4/5AC2 + BC2 = 256.

Дано: ∆АВС – прямоугольный ( ∟С = 900 ), ВМ – биссектриса ∟В. sinA= 0.8, S∆СBM =8

tgA= BC/AC, AC= BC : tgA= BC : sinA/cosA= 4√3 : 0.8 / √1-(0.8)2== 4√3 ∙ 0.6/0.8= 3√3 (см).S∆АВС= ½ AC ∙ BC= ½ ∙ 3√3 ∙ 4√3= 18 (см)2 Ответ. 18 (см)2

Реши самостоятельно:В прямоугольном треугольнике АВС высота CH, проведенная из вершины прямого угла, равна 3, АС= 5. Найти SABC Ответ. 9.375.2) В прямоугольном треугольнике АВС(∟С= 900), проведена биссектриса ВК. Найти 9√5S, где S- площадь ∆СВК. S∆ABC= 3√5, а sinA= 2/7. Ответ. 63.3) В прямоугольном треугольнике АВС(∟С= 900). Через центр О – вписанной в треугольник окружности проведён луч ВО, пересекающий катет АС в точке М. Известно, что АМ= 8√3, ∟А= ∟МВС. Найти гипотенузу. Ответ. 24.

4) Один из катетов прямоугольного треугольника равен 15см, а проекция второго катета на гипотенузу равна 16см. Найти диаметр окружности, описанной около этого треугольника. Ответ. 25см.5) Гипотенуза АВ прямоугольного треугольника АВС равна 2√22, а катет ВС равен 6.Найти длину медианы ВК. Ответ. 7.