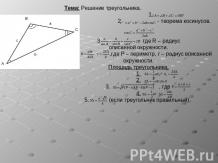
Презентация на тему: Вписанная и описанная окружность

Вписанная и описанная окружность

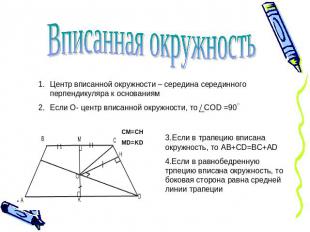
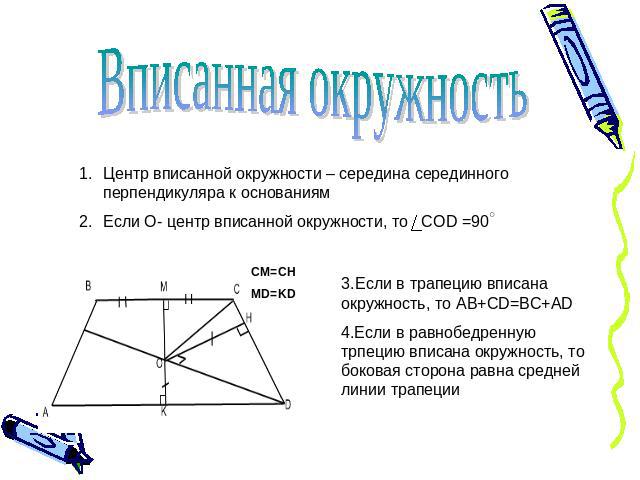
Вписанная окружность Центр вписанной окружности – середина серединного перпендикуляра к основаниямЕсли О- центр вписанной окружности, то СОD =90 3.Если в трапецию вписана окружность, то AB+CD=BC+AD4.Если в равнобедренную трпецию вписана окружность, то боковая сторона равна средней линии трапеции

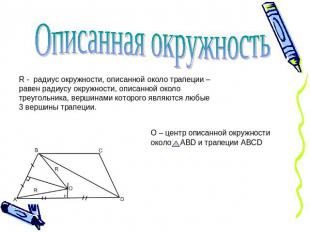
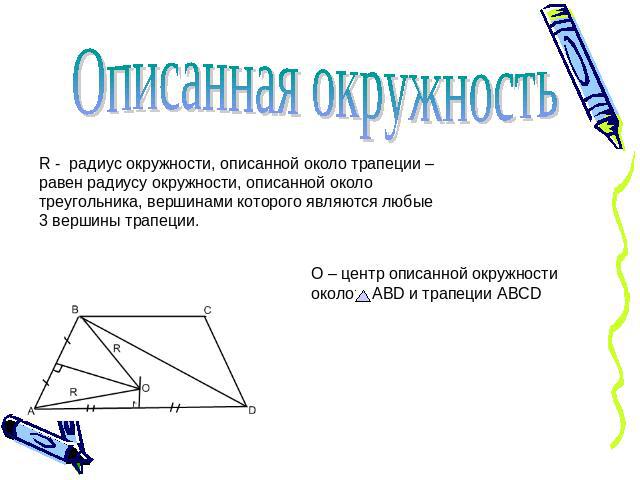
Описанная окружностьR - радиус окружности, описанной около трапеции – равен радиусу окружности, описанной около треугольника, вершинами которого являются любые 3 вершины трапеции.О – центр описанной окружности около ABD и трапеции ABCD

ЗадачиВ равнобедренной трапеции BC=9, AD=21, высота h=8. Найти диаметр описанной около трапеции окружности.Решение:Радиус R описанной окружности около трапеции – это радиус окружности около ABD D=2R, R=AH = = =6HD =21-6 = 15 HBD: DB = ABH: AB=P=

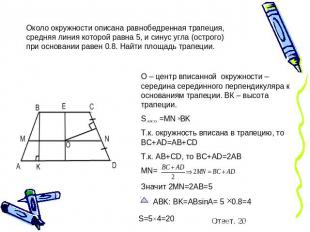
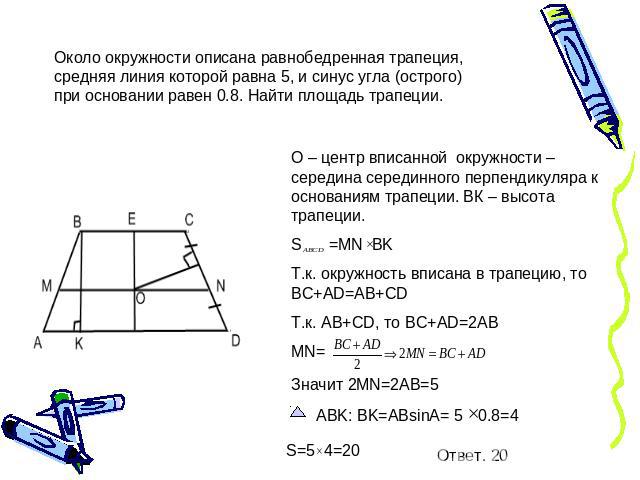
Около окружности описана равнобедренная трапеция, средняя линия которой равна 5, и синус угла (острого) при основании равен 0.8. Найти площадь трапеции.О – центр вписанной окружности – середина серединного перпендикуляра к основаниям трапеции. ВК – высота трапеции.S =MN BKТ.к. окружность вписана в трапецию, то BC+AD=AB+CDТ.к. AB+CD, то BC+AD=2ABMN=

Около трапеции описана окружность, центр которой лежит внутри трапеции. Высота трапеции равна 27, а основания 48 и 30. найти радиус окружности.КH – высота, КН – срединный перпендикулярОА=ОВ=RПусть OH=х, тогда ОК=КН-ОН=27-х AOH: AO

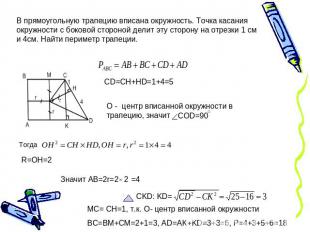
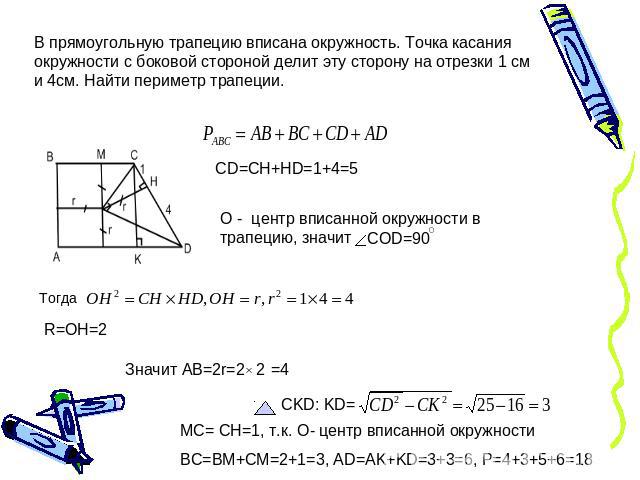
В прямоугольную трапецию вписана окружность. Точка касания окружности с боковой стороной делит эту сторону на отрезки 1 см и 4см. Найти периметр трапеции.O - центр вписанной окружности в трапецию, значит MC= CH=1, т.к. O- центр вписанной окружностиBC=BM+CM=2+1=3, AD=AK+KD=3+3=6, P=4+3+5+6=18

Решить самостоятельно1. Один из углов равнобедренной трапеции равен 60 , а её площадь равна Найти радиус окружности, вписанной в эту трапецию.2.Окружность описана около равнобедренной трапеции ABCD с основанием AD=15 AC и BD образуют с боковой стороной AB углы ВАС= , ABD= также, что sin3.Около трапеции описана окружность, центр которой лежит на основании AD.Найти радиус описанной окружности.4.Равнобедренная трапеция описана около окружности радиуса 2. Найти площадь трапеции, если косинус угла при большем основании трапеции равен 0,6 5.Средняя линия прямоугольной трапеции равна 9,а радиус вписанной окружности в неё равен 4. Найти большее основание трапеции.