Презентация на тему: Построение сечений многогранников

Построение сечений многогранников

Работа выполнена ученицей 10 А классаМОУ СОШ №7Кудряшовой КсениейРуководители проекта:учитель математики школы №7 Дулевич Галина Владимировнаучитель информатики школы № 7 Дорофеева Оксана Викторовна

Виды многогранников

Тетраэдр

Параллелепипед

Пирамида

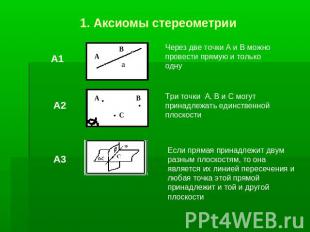
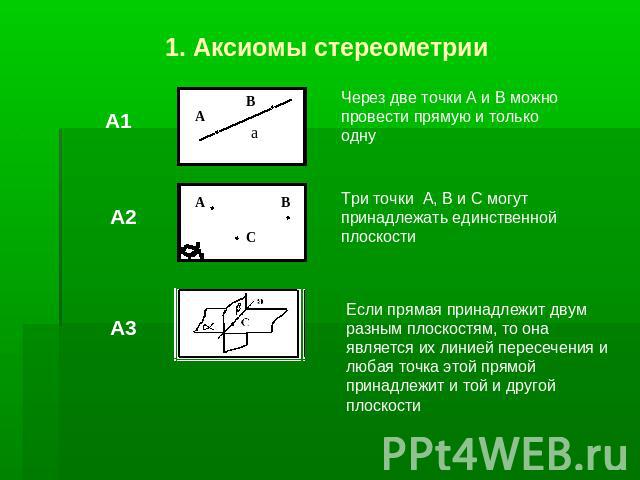
1. Аксиомы стереометрииЧерез две точки А и В можно провести прямую и только однуТри точки А, В и С могут принадлежать единственной плоскостиЕсли прямая принадлежит двум разным плоскостям, то она является их линией пересечения и любая точка этой прямой принадлежит и той и другой плоскости

2. Следствия из аксиом стереометрииЕсли две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.Через прямую и не лежащую на ней точку можно провести плоскость и при том только одну. Через две пересекающиеся прямые можно провести плоскость и при том только одну.

Задачу построения сечения многогранников рассмотрим на примерах: 1.Построить сечение параллелепипеда ABCDA1B1C1D1 , проходящее через ребро СС1 и точку пересечения диагоналей грани АА1DD1. 2.Построить сечение тетраэдра KLMN плоскостью, проходящей через ребро KL и середину А ребра MN. 3.Построить сечение пирамиды плоскостью, проходящей через три заданные точки.

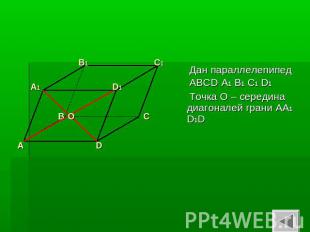
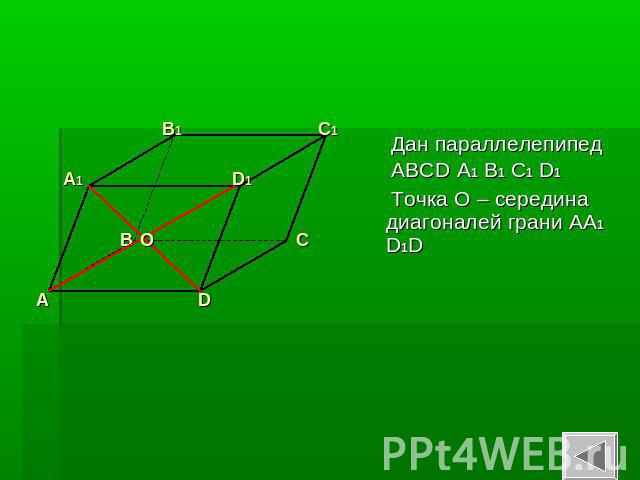
Дан параллелепипед АВСD A1 B1 C1 D1 Точка О – середина диагоналей грани АА1 D1D

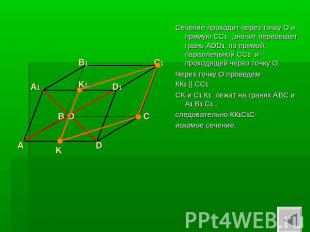
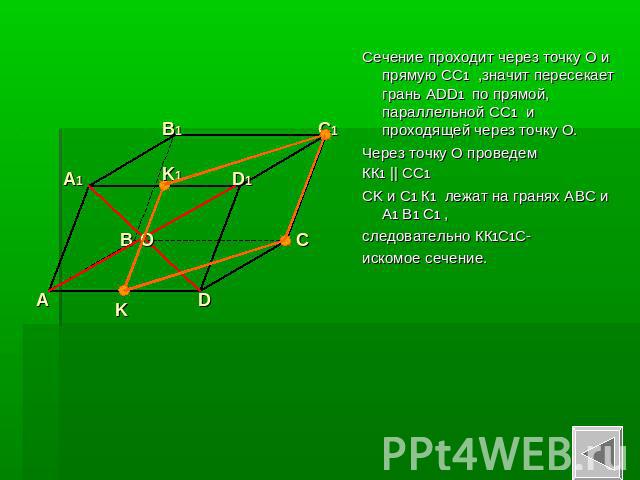
Сечение проходит через точку О и прямую СС1 ,значит пересекает грань ADD1 по прямой, параллельной СС1 и проходящей через точку О.Через точку О проведем КК1 || CC1CK и С1 К1 лежат на гранях АВС и А1 В1 С1 , следовательно КК1С1С- искомое сечение.

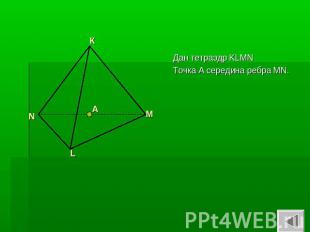
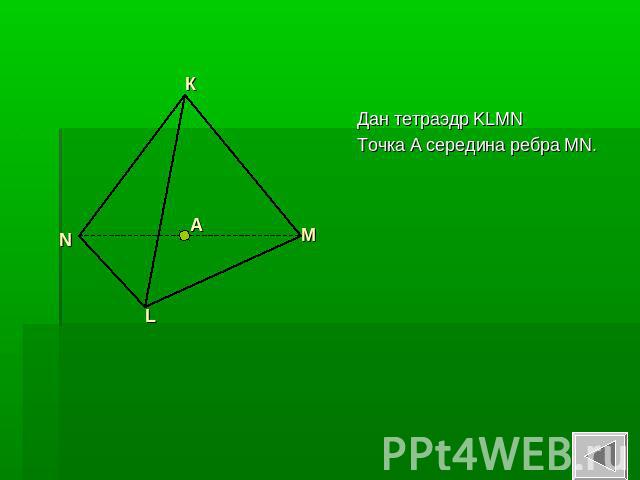
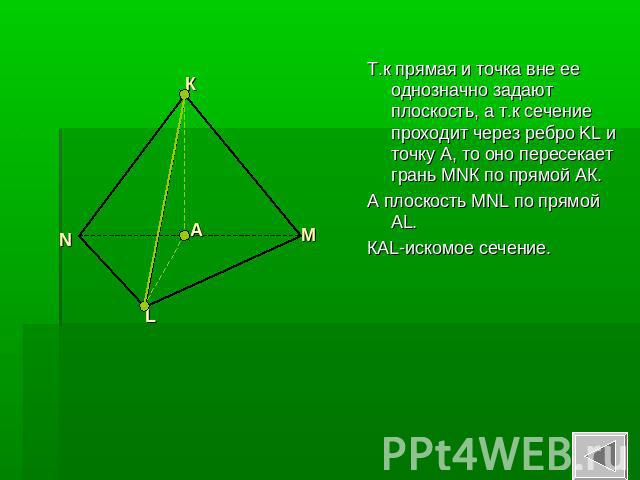
Дан тетраэдр KLMNТочка А середина ребра MN.

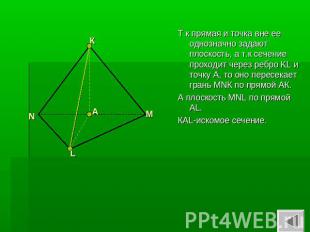
Т.к прямая и точка вне ее однозначно задают плоскость, а т.к сечение проходит через ребро KL и точку А, то оно пересекает грань MNК по прямой АК. А плоскость MNL по прямой AL.КАL-искомое сечение.

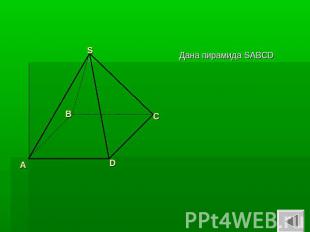
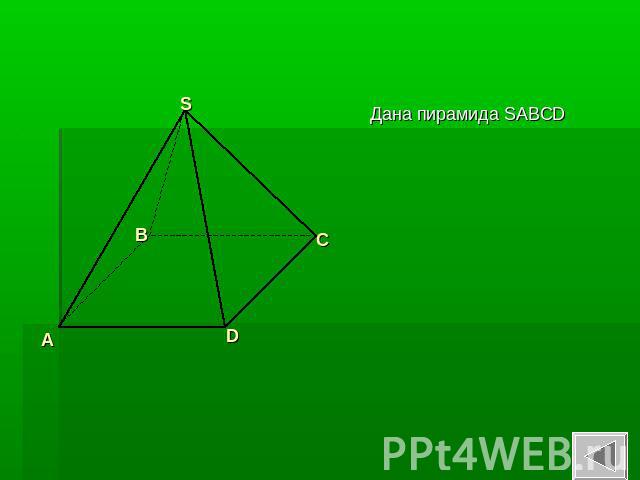
Дана пирамида SABCD

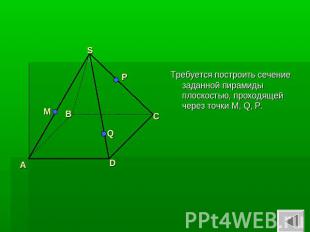
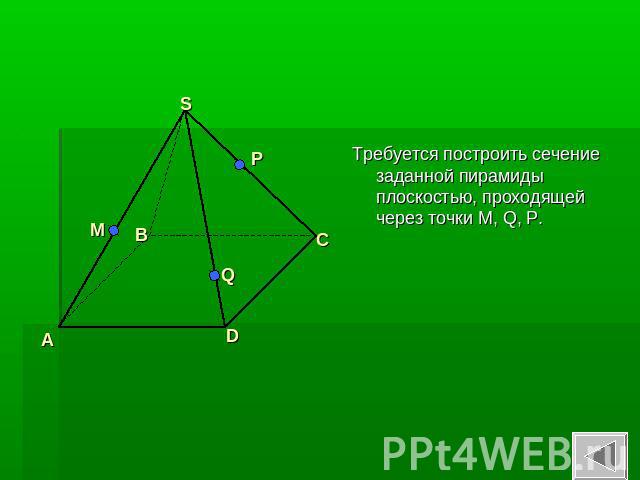
Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки M, Q, P.

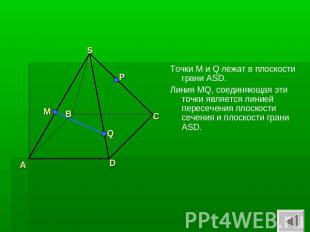
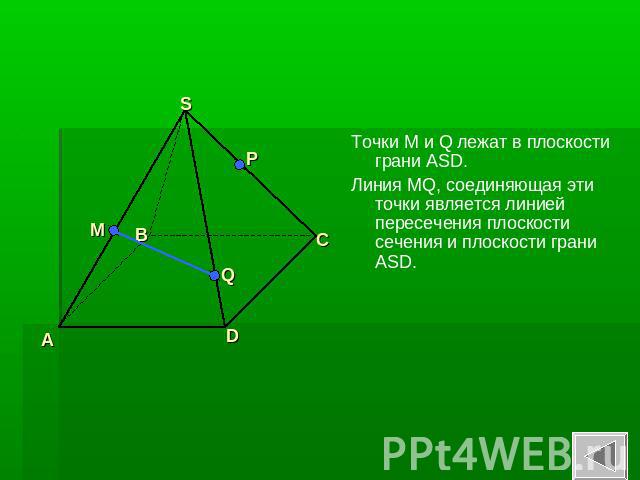
Точки M и Q лежат в плоскости грани ASD.Линия MQ, соединяющая эти точки является линией пересечения плоскости сечения и плоскости грани ASD.

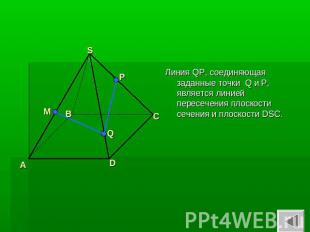
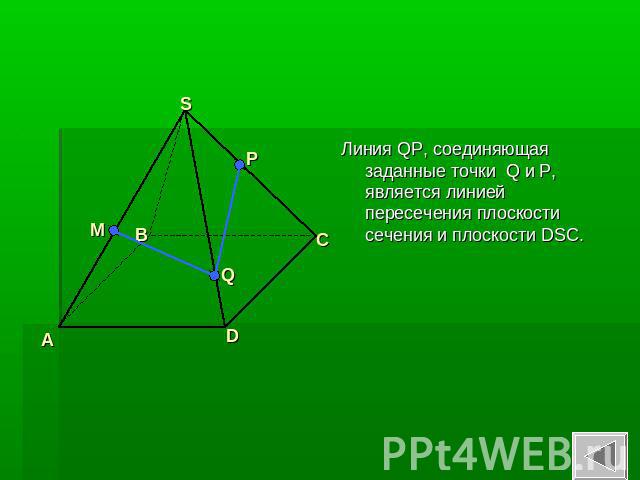
Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения и плоскости DSC.

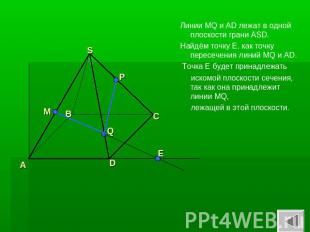
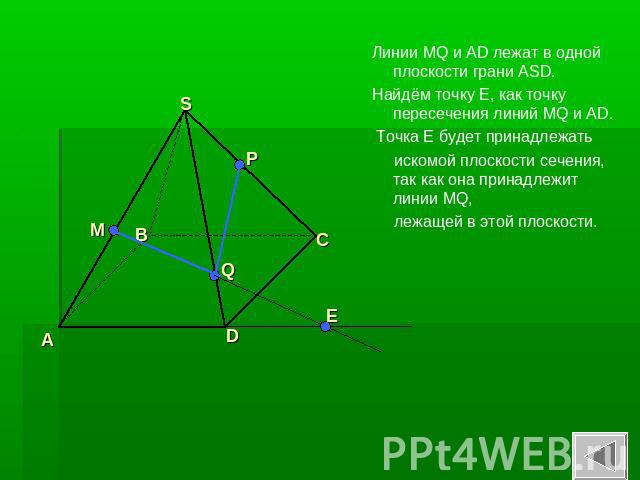
Линии MQ и AD лежат в одной плоскости грани ASD. Найдём точку Е, как точку пересечения линий MQ и AD. Точка Е будет принадлежать искомой плоскости сечения, так как она принадлежит линии MQ, лежащей в этой плоскости.

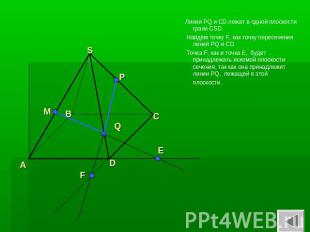
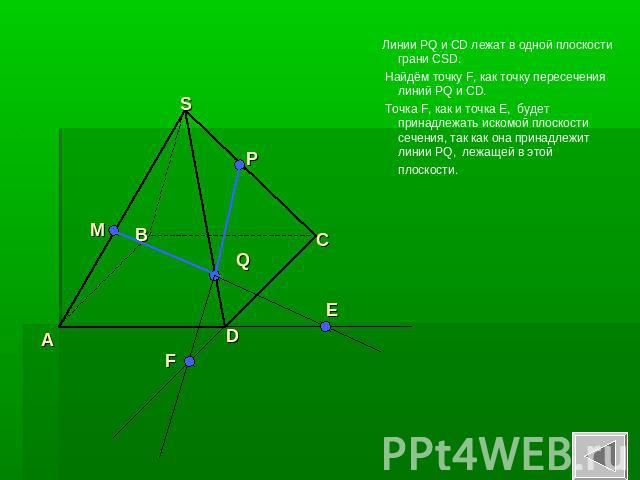
Линии PQ и CD лежат в одной плоскости грани CSD. Найдём точку F, как точку пересечения линий PQ и CD. Точка F, как и точка Е, будет принадлежать искомой плоскости сечения, так как она принадлежит линии PQ, лежащей в этой плоскости.

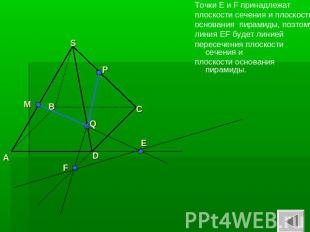
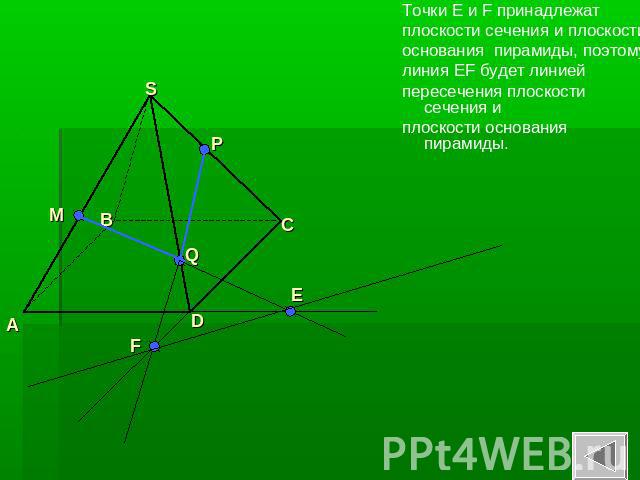
Точки Е и F принадлежат плоскости сечения и плоскости основания пирамиды, поэтому линия EF будет линией пересечения плоскости сечения иплоскости основания пирамиды.

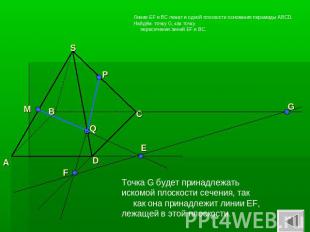
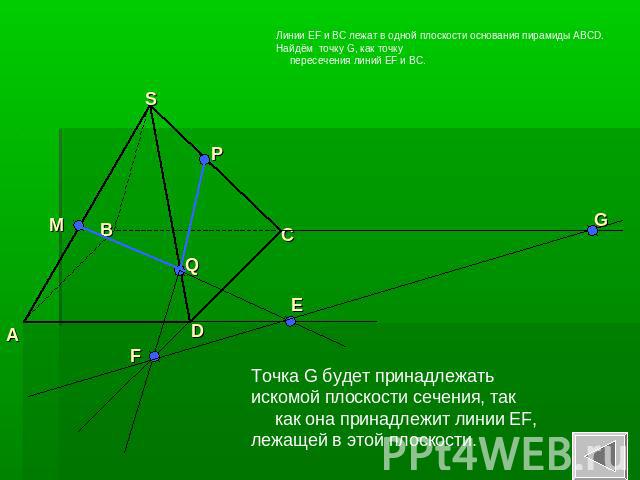
Линии EF и BC лежат в одной плоскости основания пирамиды ABCD. Найдём точку G, как точку пересечения линий EF и BC. Точка G будет принадлежать искомой плоскости сечения, так как она принадлежит линии EF, лежащей в этой плоскости.

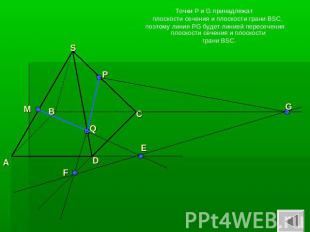
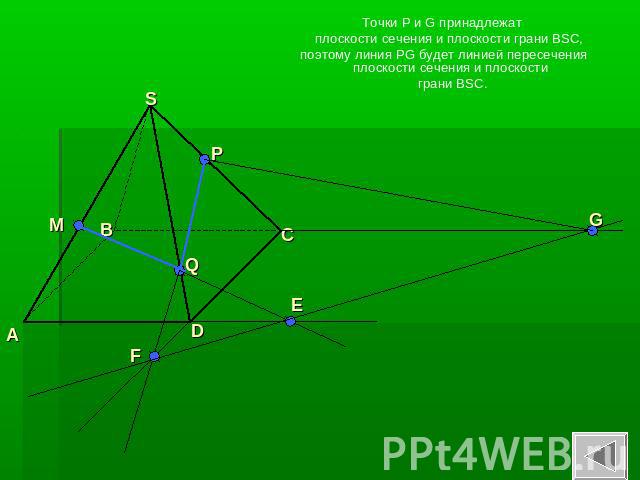
Точки P и G принадлежат плоскости сечения и плоскости грани BSC, поэтому линия PG будет линией пересечения плоскости сечения и плоскости грани BSC.

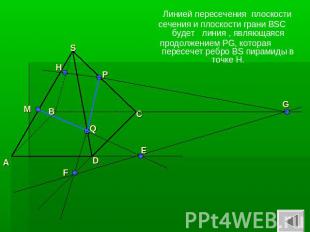
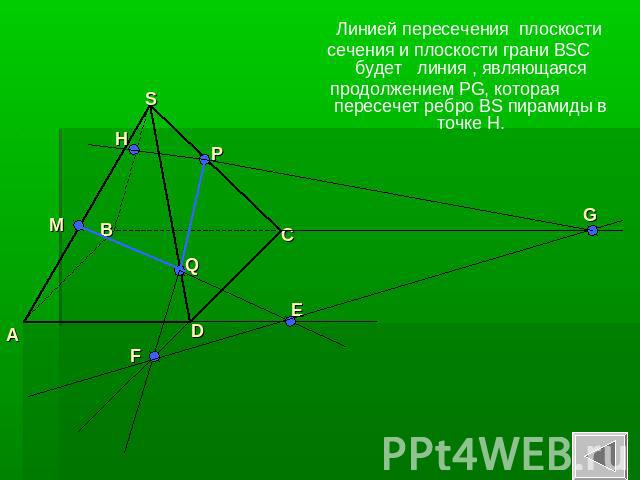
Линией пересечения плоскости сечения и плоскости грани BSC будет линия , являющаяся продолжением PG, которая пересечет ребро BS пирамиды в точке H.

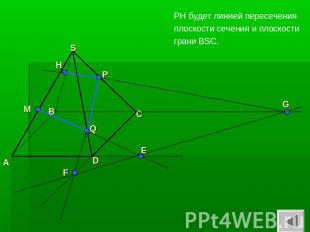
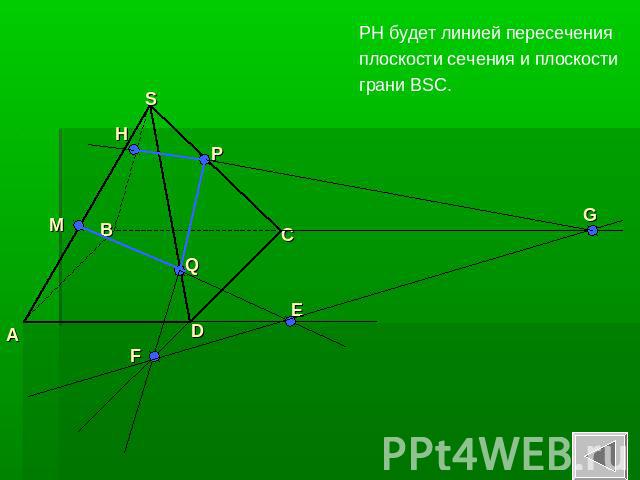
PH будет линией пересечения плоскости сечения и плоскости грани BSC.

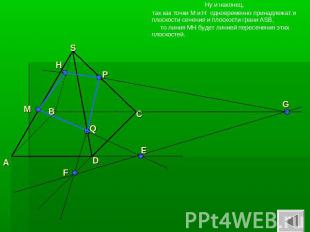
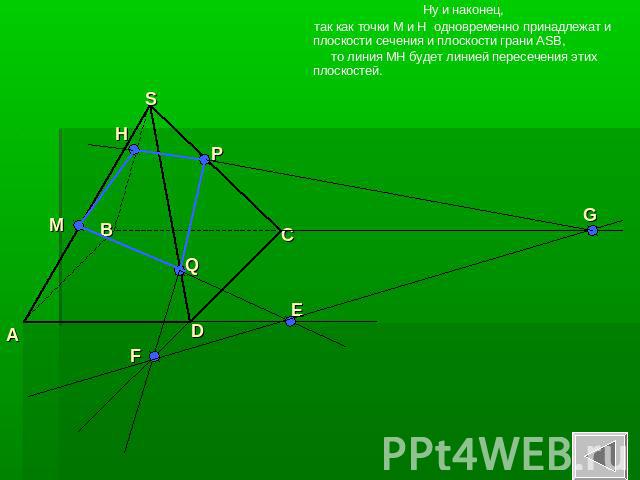
Ну и наконец, так как точки M и H одновременно принадлежат и плоскости сечения и плоскости грани ASB, то линия MH будет линией пересечения этих плоскостей.

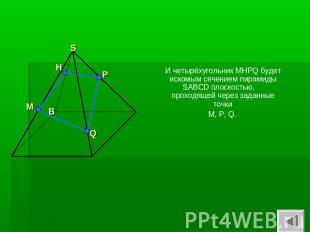
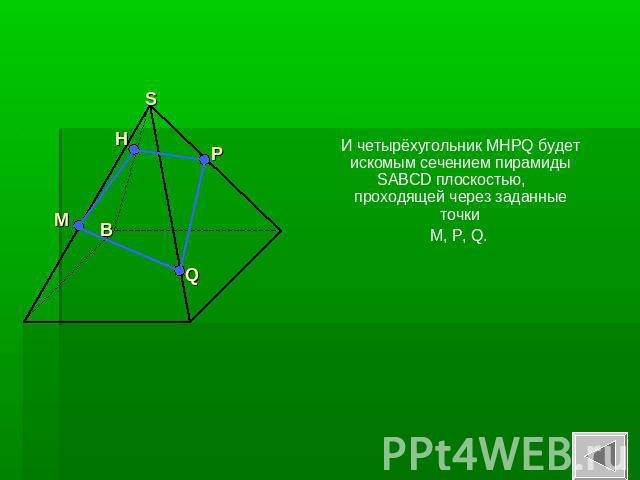
И четырёхугольник MHPQ будет искомым сечением пирамиды SABCD плоскостью, проходящей через заданные точки M, P, Q.