Презентация на тему: Фракталы: наука и искусство XXI века

«Фракталы: наука и искусство XXI века » Управление образования административного городского округа – город Волжский Волгоградской областиМуниципальное образовательное учреждениесредняя общеобразовательная школа № 14 «Зеленый шум» Автор Боржес А.-М. Руководитель Лопатина И. С.
Развитие геометрии, используемой для описания природных процессов Классическая геометрия Фрактальная геометрия

Фрактальные структуры в природе
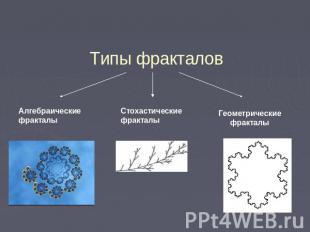
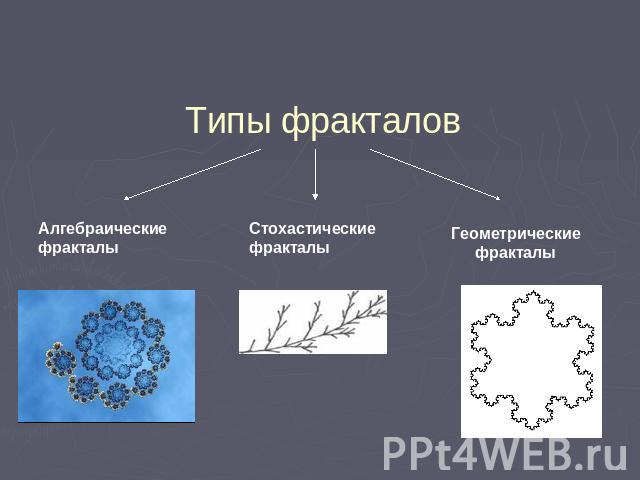
Типы фракталов Алгебраические фракталы Стохастические фракталы Геометрические фракталы

Алгебраические фракталы Самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двумерные процессы.

Стохастические фракталы Образуются в случае случайной перемены в итерационном процессе параметров фрактала. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Геометрические фракталы 1). Звезда Коха2). Фрактал Вацлава Серпинского («Ковер Серпинского»)3). Фрактальная кривая Д.Пеано 4). “Кривая дракона” Э. Хейуэея
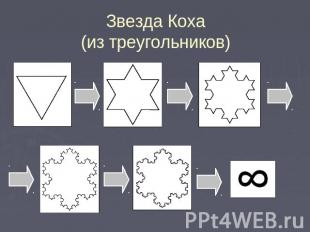
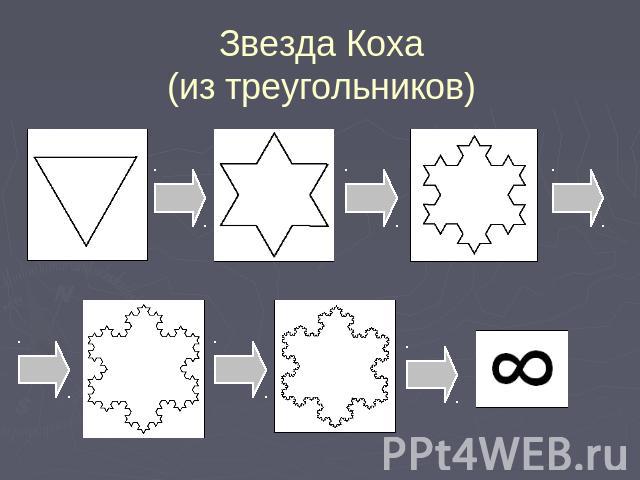
Звезда Коха(из треугольников)
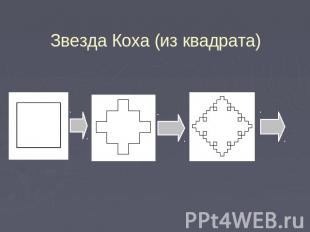
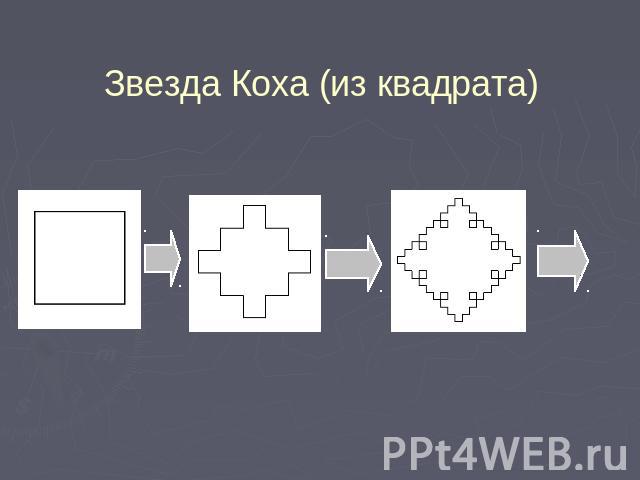
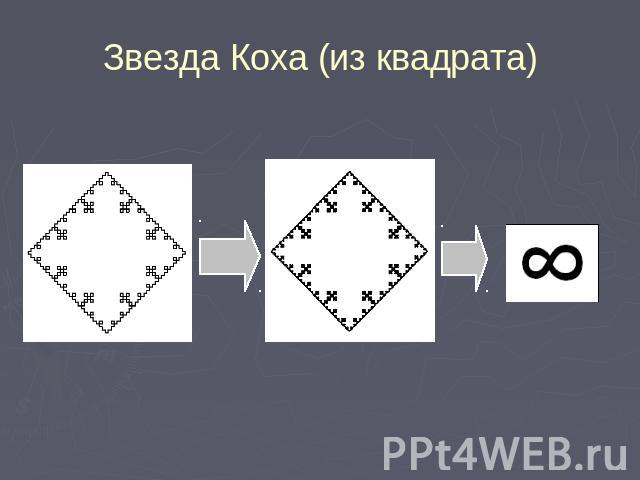
Звезда Коха (из квадрата)
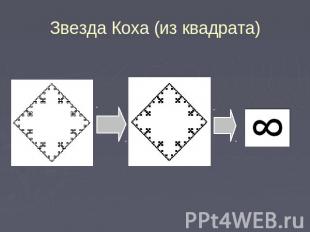
Звезда Коха (из квадрата)
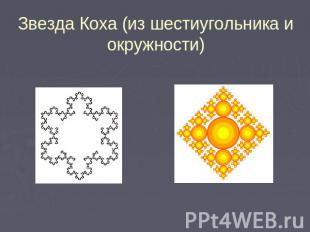
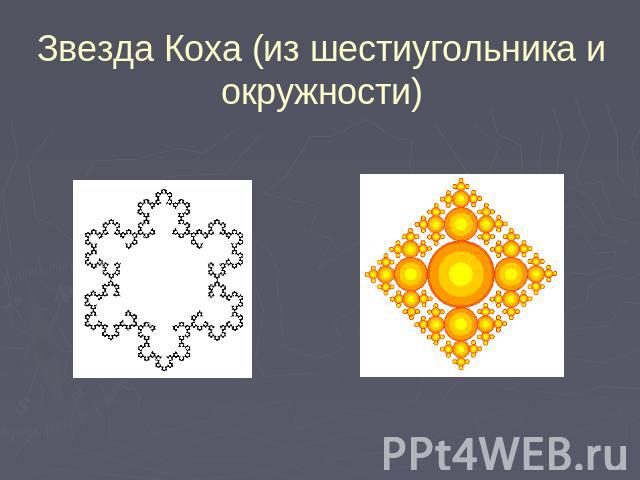
Звезда Коха (из шестиугольника и окружности)
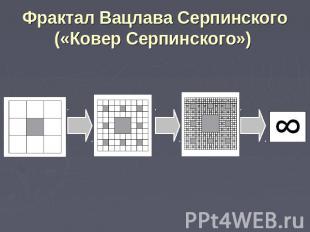
Фрактал Вацлава Серпинского («Ковер Серпинского»)

Фрактал Вацлава Серпинского («Салфетка Серпинского») Получается из треугольника последовательным вырезанием серединных правильных треугольников
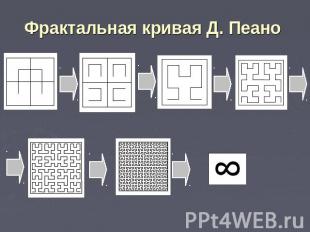
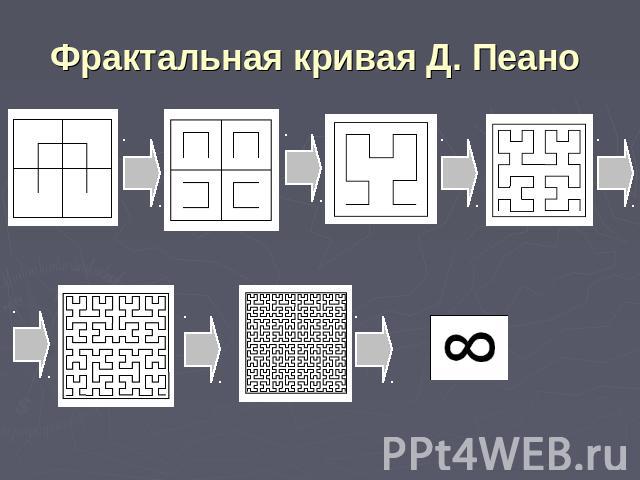
Фрактальная кривая Д. Пеано
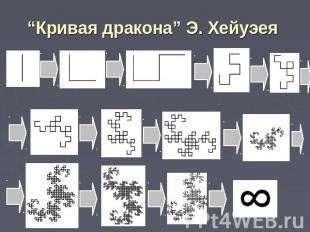
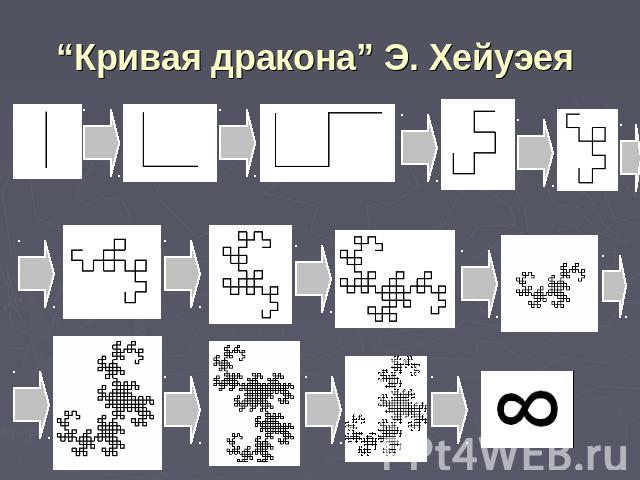
“Кривая дракона” Э. Хейуэея

Список литературы 1. Азевич А.И. Фракталы: геометрия и искусство М.: Мир, 1995. 2. Бондаренко В.А., Дольников В.Л. Фрактальное сжатие изображений // Автоматика и телемеханика. – 1994. – № 5.3. Витолин Д.П. Применение фракталов в машинной графике // Computerworld – Россия. – 1995. – № 15.4. Волошинов А.В. Математика и искусство – М.: Просвещение, 2000.1. Вишик М.И. Фрактальная размерность множеств. Соросовский образовательный журнал. № 1, 1998.2. Жиков В.И. Фракталы. Соросовский образовательный журнал. № 12, 1996.5. Кроновер Р.М., Фракталы и хаос в динамических системах. Основы теории.6. Мандельброт Б. Фрактальная геометрия природы.7. Морозов А.Д., Введение в теорию фракталов.8. Пайттен Х.Щ., Рихтер П.Х. Красота фракталов. Пер. с англ. – М.: Мир, 1993.9. С. Пейперт Переворот в сознании: дети, компьютеры и плодотворные идеи. – М.: Педагогика, 1989.10. Федер Е. Фракталы. Пер. с англ. – М.: Мир, 1991.11. Шабаршин А.А. Введение во фракталы. – Екатеринбург, 1998.12. Шредер М., Фракталы, хаос, степенные законы.