Презентация на тему: Удивительный квадрат (8 класс)

Муниципальное учреждение ЗАТО Северск«Средняя общеобразовательная школа №84»«Удивительный квадрат» Руководители: Подколзина О.Е. учитель математики Выполнила: Подколзина А.А. 8 «А» класс ЗАТО Северск 2006г.

Содержание: Определения квадрата и свойства квадратаТеорема ПифагораПерегибая лист бумаги, оригами.Танграм и другие головоломки, связанные с квадратомРазрезание квадрата.Литература.

Удивительный квадрат.

КвадратКвадрат- это самая совершеннаягеометрическая фигура. Онвстречается в самых разныхпроизведениях искусства: отоснований египетских пирамид до«Чёрного квадрата» Малевича .

ЗАМЕЧАТЕЛЬНЫЕ СВОЙСТВА КВАДРАТА У квадрата есть ряд интересных свойств. Так, например, если необходимо забором данной длины огородить четырехугольный участок наибольшей площади, то следует выбрать этот участок в виде квадрата.

ОПРЕДЕЛЕНИЯ КВАДРАТАУ квадрата все стороныравны, как и у ромба.Только еще все углыпрямые. Значит, квадрат -это ромб с прямыми углами.

ОПРЕДЕЛЕНИЯ КВАДРАТАУ квадрата, как и упрямоугольника, все углыпрямые. Только еще всестороны равны. Значит,квадрат -это прямоугольник,у которого все стороны равны.

ОПРЕДЕЛЕНИЯ КВАДРАТАУ квадрата, как и упараллелограмма, стороныпопарно параллельны.Только еще все они равны ивсе углы прямые. Значит,квадрат-это параллелограммс прямыми углами, всестороны которого равны.

Теорема Пифагора: В математике квадрат впервые появился в теореме Пифагора.Теорема Пифагора: квадрат, построенный на гипотенузепрямоугольного треугольника, равновеликсумме квадратов, построенных на егокатетах.

Простейшее доказательство теоремы Пифагора. Простейшее доказательство получается в простейшем случае равнобедренного треугольника. Достаточно посмотреть на мозаику равнобедренных прямоугольных треугольников. Для треугольника ABC: квадрат, построенный на гипотенузе АС, содержит четыре исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.

Головоломки, связанные с квадратом. Самый обыкновенный, хорошо всем знакомый квадрат может весь без остатка превратиться в другую фигуру или несколько других фигур, но предварительно должен быть разрезан на определенные части. Очень остроумно разрезал квадрат китайский ученый Та-нг:

Перегибая лист бумаги. Среди множества возможных действий с бумагой особое место занимает операция её перегибания. Одним из достоинств является то, что её можно производить, не имея под рукой никаких дополнительных инструментов – ни линейки, ни карандаша, ни циркуля.

ПОСТРОЕНИЯ ПРИ ПОМОЩИ ПЕРЕГИБАНИЯ КВАДРАТНОГО ЛИСТА БУМАГИ Согните квадратный лист бумаги вдвое произвольным образом и сделайте два прямых разреза . Какой формы получится отверстие в зависимости от угла разреза?

Построения при помощи перегибаний квадратного листа бумаги. Из прямоугольника квадрат. Из бумаги вырезан прямоугольник. Получите из него квадрат со стороной, равной меньшей стороне прямоугольника. Решение: Перегнем прямоугольный лист бумаги по биссектрисе одного из углов BAD, т.е. так, чтобы сторона AB прямоугольника ABCD пошла по соседней с ней стороне AD, а линия сгиба пересекла какую-то третью сторону в точке E. Пусть меньшая сторона AB оказалась наложенной сверху на большую сторону AD. Тогда, перегнув нижнюю часть листа вдоль линии BE, мы получим квадрат ABEF.

ОРИГАМИ Оригами- это чудо. Оригами- складывание фигурок из бумаги. Создание разнообразных фигурок – настоящее искусство. Оригами распространилось по всему свету. Древнее искусство пришло из Китая, откуда Япония черпала духовные богатства. «Великий квадрат не имеет предела» Квадрат выступает как оригинальный конструктор; его трансформируют бесконечно.

ТАНГРАМ И ДРУГИЕ ГОЛОВОЛОМКИ , СВЯЗАННЫЕ С КВАДРАТОМ ТАНГРАМ ПЕНТАМИНО ТЕТРАМИНО ПОЛИМИНО СТОМАХИОН

ТАНГРАМ Если разрезать квадрат, как показано на рисунке, то получится популярная китайская головоломка ТАНГРАМ, которую в Китае называют «чи чао ту», т. е. умственная головоломка из семи частей.

Задача. Постройте заданную фигуру, используя все семь танов.Щелкнув мышью вы увидите решение.

ПЕНТАМИНО Это игра была придумана в 50-х годах ХХ в. американским математиком С. Голомбом, она заключается в складывании различных фигур из заданного набора пентамино. Набор содержит 12 фигурок, каждая из которых составлена из 5 одинаковых квадратов. Используя набор пентамино сложите данные фигуры.

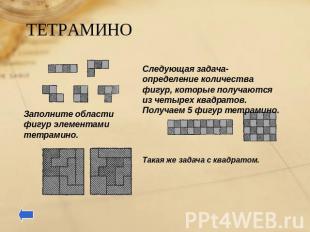
ТЕТРАМИНО Следующая задача- определение количества фигур, которые получаются из четырех квадратов. Получаем 5 фигур тетрамино. Заполните области фигур элементами тетрамино. Такая же задача с квадратом.

СТОМАХИОН Игра стомахион была известна еще до нашей эры. Создателем игры является Архимед. Сделать игру несложно, необходимо взять прямоугольник, одна сторона которого в два раза больше другой.

ПОЛИМИНО Термин "полиомино" ввёл в употребление известный математик Соломон В. Голомб. В своей статье "Шахматные доски и полиомино" Голомб определил полиомино как односвязную фигуру, составленную из квадратов. Шахматист сказал бы, добавляет Голомб, что фигуры составлены "ходом ладьи", потому что ладья могла бы обойти их за конечное число ходов.

Разрезание квадратного листа бумаги. На языке геометрии разрезание квадрата значит: найти те геометрические построения, при помощи которых разрезается квадрат, и доказать, что из полученных частей может быть составлена требуемая фигура.

Задачи на разрезания квадрата. Задача №1. Разрежьте квадрат на четыре одинаковые (по форме и размеру) части, в каждой из которых один крестик и один кружок.Разрезать нужно по клеткам. Щелкнув мышью вы увидите решение.

Задача №2. Разрежьте приведенную фигуру на 2 части и сложите из получившихся частей квадрат .Щелкнув мышью вы увидите решение задачи.

Задача №3. Как можно превратить квадрат в 8 равных квадратов? Решение: Разрезая данный квадрат ABCD по диагоналям AC и BD, которые пересекутся в точке О, получим четыре равных прямоугольных треугольника AOB, BOC, COD, DOA , из которых можно составить два квадрата. В свою очередь каждый из полученных квадратов без труда разрезается на 4 равных квадрата.

Задача №4. Разрежьте квадрат на пять прямоугольников так, чтобы у любых двух соседних прямоугольников стороны не совпадали.

Литература: 1. Квадрат // Квант. – 1989 - №5 – с. 40.2. Кордемский Б.А., Русалев Н.В. Удивительный квадрат. – М.: Столетие, 1994.3. Лоповок Л.М. Тысяча проблемных задач по математике: Книга для учащихся. – М.: Просвещение, 1995, с. 38.4. Сергеев И.Н. и др. Примени математику. – М.: Наука, 1989, с. 172.5. Волошинов А.В. Пифагор. – М.: Просвещение, 1993, с. 165.6. Ефимов О., Морозов В., Шафрин Ю. Курс компьютерной технологии. – М.: АБФ, 1998, с. 492.