Презентация на тему: Треугольник, простейший и неисчерпаемый

Треугольник, простейший и неисчерпаемый. Задачи для подготовки к ЕГЭ. Авторы творческой работы:Учащиеся 9 «Г» класса МОУ СОШ №96 г. Краснодара Головнин Александр, Коровин Илья , Воробьев Александр.Руководитель проекта учитель математики Сосна Ольга Александровна.

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.

Аннотация к работе. Цель нашей работы - помочь учащимся подготовиться к итоговой аттестации. Для успешного выполнения экзаменационных заданий необходимы твердые знания основных геометрических фактов и некоторый практический опыт . Работа может быть полезна учащимся не только 9 класса, но и 8 и 10 классов, которые в будущем будут сдавать ЕГЭ. Кроме того, надеемся , что наша презентация послужит хорошим подспорьем для учителей математики при проведении уроков по темам , связанным с треугольником.Текст на слайдах появляется по щелчку мышки, есть время подумать над задачей , проанализировать условие, потом сравнить свое решение с нашим. Презентация содержит историческую справку о треугольниках и краткий справочный материал.

Содержание . Задача №1Задача №2Задача №3 Задача №4Задача №5Задача №6Задача №7Задача №8Задача №9 Справочный материал

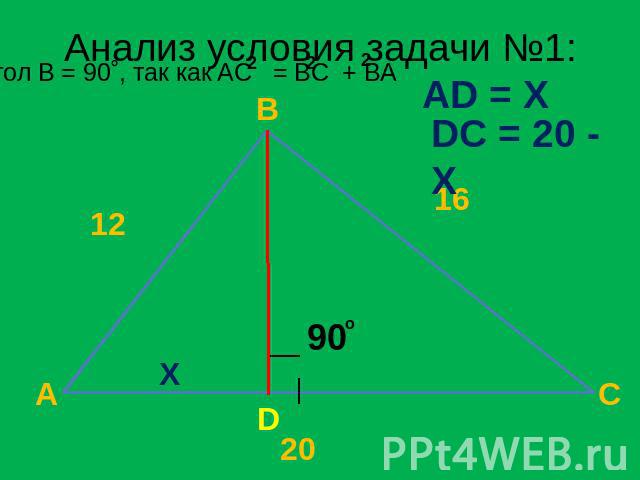
Задача №1 Стороны треугольника равны 12 м., 16 м., и 20 м.. Найдите его высоту, проведенную из вершины большего угла. Дано: ABC - треугольник AB = 12 м. AC = 20 м. BD = ? м.

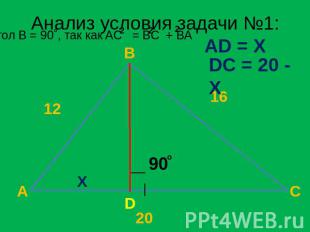
Анализ условия задачи №1: Угол B = 90˚, так как AC = BC + BA AD = X DC = 20 - X

Решение задачи №1: Рассмотрим треугольник ABD BD = 12 - X 12 – X = X(20 – X) BD = X(20 – X)

Решение задачи №1: 144 – X = 20X – X BD = 7,2(20 – 7,2) = 92,16 BD = 9,6 7,5 – X = 0 X = 7,2

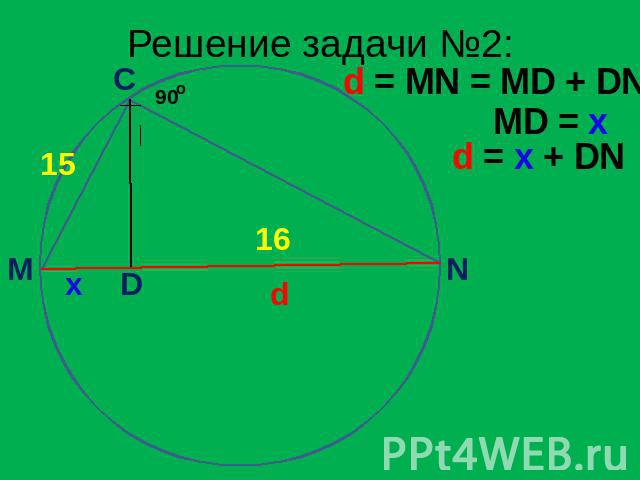
Задача №2 Один из катетов прямоугольного треугольника равен 15, проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника. Дано: MCN – вписанный треугольник DN = 16 Найти: MN

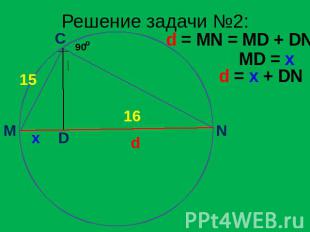
Решение задачи №2: d = MN = MD + DN MD = x d = x + DN

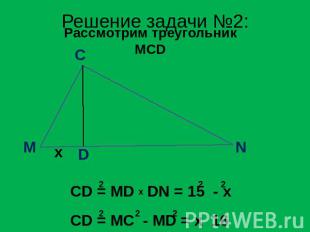
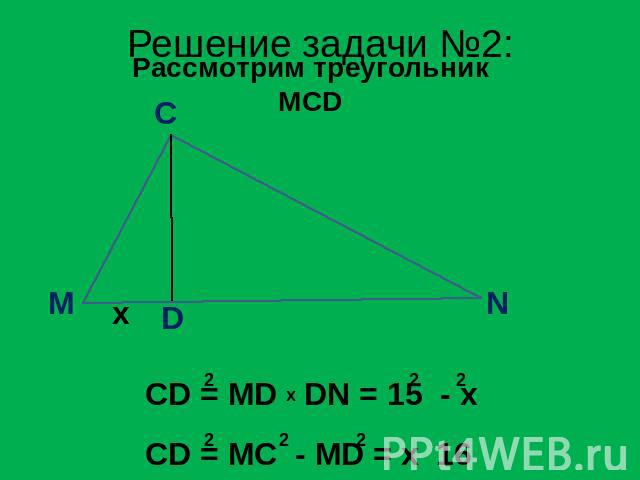
Решение задачи №2: Рассмотрим треугольник MCD CD = MD DN = 15 - x CD = MC - MD = x 16

Решение задачи №2: 15 - x = x 16 x + 16x – 255 = 0 D = 256 + 900 = 1156 d = x + DN d = 9 + 16 = 25

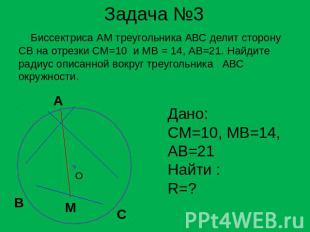
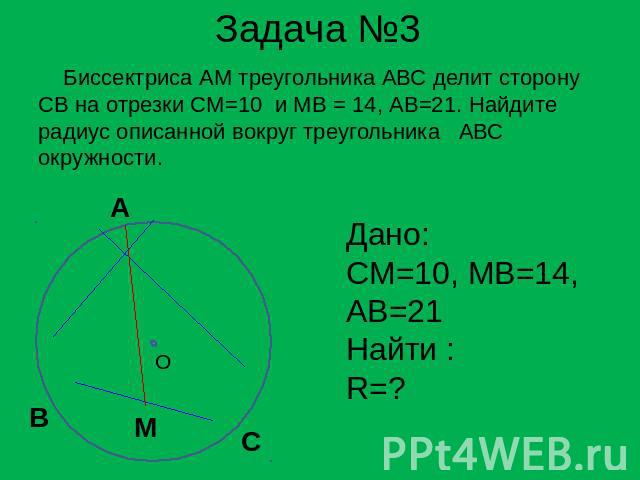
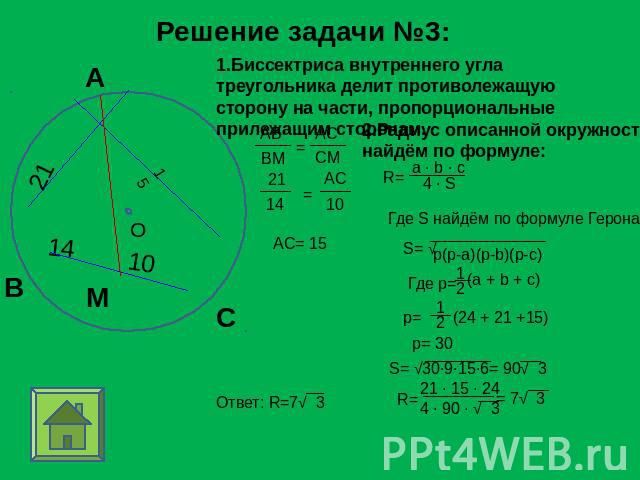
Задача №3 Биссектриса АМ треугольника АВС делит сторону СВ на отрезки СМ=10 и МВ = 14, АВ=21. Найдите радиус описанной вокруг треугольника АВС окружности. Дано:CM=10, MB=14,AB=21Найти :R=?

Решение задачи №3: 1.Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. 2.Радиус описанной окружностинайдём по формуле:

Задача №4: Найдите радиус окружности, вписанной в остроугольный треугольник ABC, если высота BH равна 12 и известно , что О – центр , вписанной окружности Найти: r

Решение задачи №4: 2. По определению синуса из ∆BHC , где BHC=90( по условию BHAC)sinA = = Ответ : r = 4

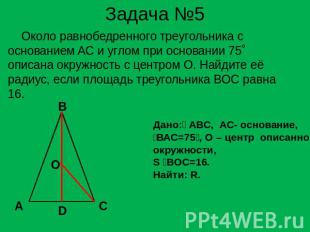
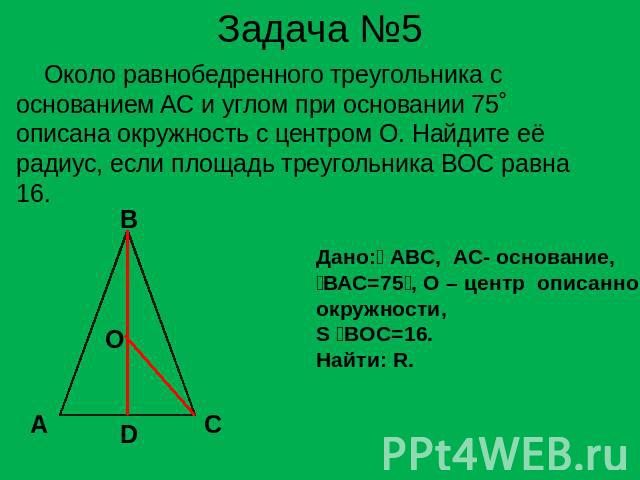
Задача №5 Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром О. Найдите её радиус, если площадь треугольника BOC равна 16. Дано: АВС, АС- основание,ВАС=75, О – центр описаннойокружности, S BОC=16.Найти: R.

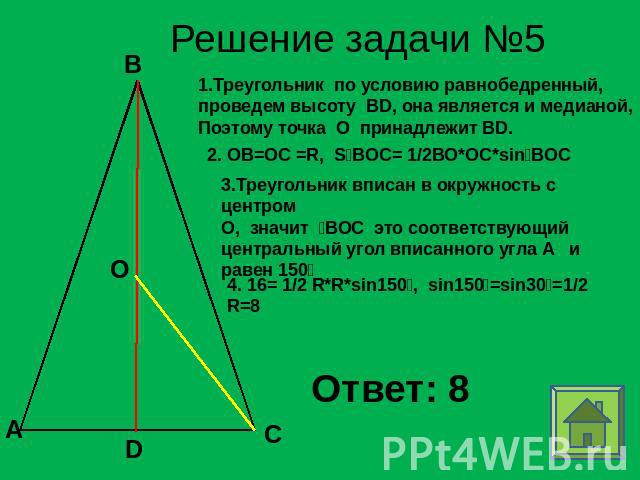
Решение задачи №5 1.Треугольник по условию равнобедренный, проведем высоту BD, она является и медианой,Поэтому точка О принадлежит BD. 2. ОВ=ОС =R, SBOC= 1/2ВО*ОС*sinBOC 3.Треугольник вписан в окружность с центромО, значит ВОС это соответствующий центральный угол вписанного угла А и равен 150 4. 16= 1/2 R*R*sin150, sin150=sin30=1/2R=8 Ответ: 8

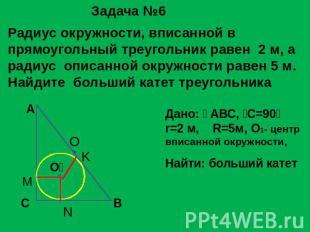
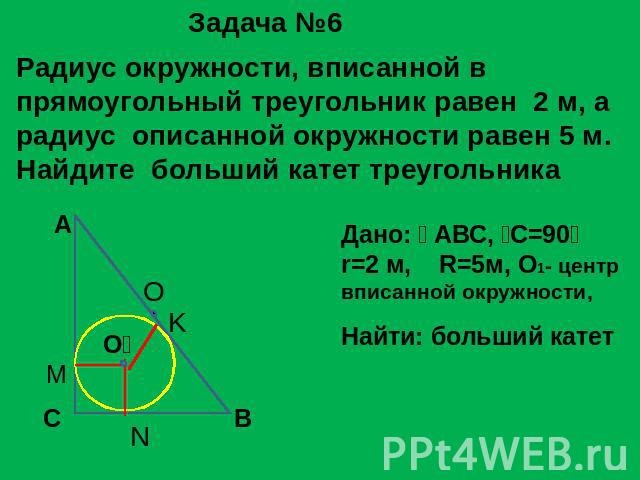
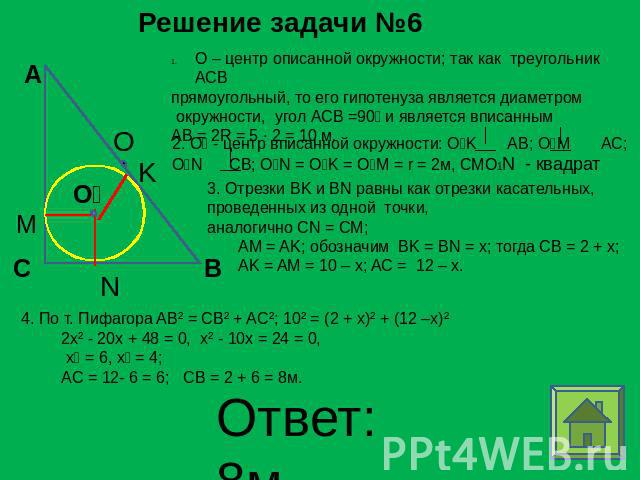
Задача №6 Радиус окружности, вписанной в прямоугольный треугольник равен 2 м, а радиус описанной окружности равен 5 м.Найдите больший катет треугольника Дано: АВС, С=90r=2 м, R=5м, О1- центрвписанной окружности, Найти: больший катет

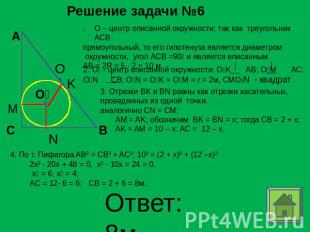
Решение задачи №6 О – центр описанной окружности; так как треугольник АСВпрямоугольный, то его гипотенуза является диаметром окружности, угол АСB =90 и является вписанным AB = 2R = 5 ∙ 2 = 10 м. 2. O₁ - центр вписанной окружности: O₁K AB; O₁M AC;O₁N CB; O₁N = O₁K = O₁M = r = 2м, СМО1N - квадрат 3. Отрезки BK и BN равны как отрезки касательных,проведенных из одной точки, аналогично CN = CM; AM = AK; обозначим BK = BN = x; тогда CB = 2 + x; AK = AM = 10 – x; AC = 12 – x.2x² - 20x + 48 = 0, x² - 10x = 24 = 0, x₁ = 6, x₂ = 4; AC = 12- 6 = 6; CB = 2 + 6 = 8м.

Задача №7 Периметр прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности - 6 м.Найдите диаметр описанной окружности. ABC – треугольникP=72 C=90⁰r = 6 мНайти d описанной окружности.

Решение задачи №7: ∆АВС – прямоугольный ; угол C = 90˚, Значит диаметр описанной окружности совпадает с гипотенузой т.е. d=AB 2. О – центр вписанной окружности, ON = ОМ = r = 6По свойству касательной ON CВ , ОМ ВС ; значит СМ=СN, как отрезки касательных к окружности с центром О, проведенных из одной точки, итак , четырехугольникCMON – квадрат со стороной ОМ = 6. 3. Обозначим отрезки BN = BK = x (OK AB)OK=r , ВN=ВК как отрезки касательных AM = MK = yP ∆АВС = AC + AB + CB, но АС = 6+у, АВ = x + у СВ = 6+х P ∆АВС = 6+у+х+у+6+х = 12+2х+2у = 72 (по условию)х + у = (72-12) : 2 , х + у = 30 , АВ=30

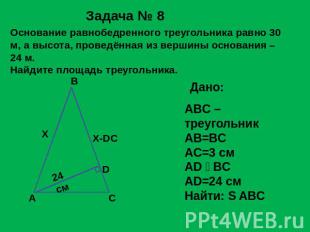
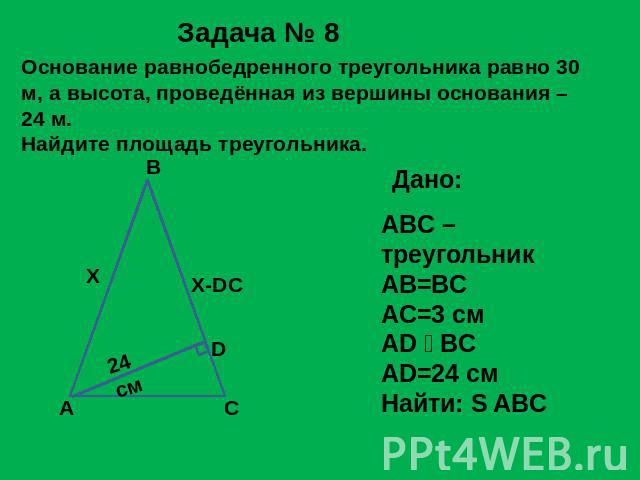
Задача № 8 Основание равнобедренного треугольника равно 30 м, а высота, проведённая из вершины основания – 24 м.Найдите площадь треугольника. ABC – треугольникAB=BCAC=3 смAD BCAD=24 смНайти: S ABC

Решение задачи №8: S ∆АВС = ½ AD ∙ BC Найдём ВС, обозначим АВ = ВС = х, тогда DB = x - DC 2. Из ∆АВС найдём DC 3. ∆ABD по т. Пифагора имеем: (x – 18) = x - 2436x = 324 + 5764x = 100X = 25 S ∆АВС = ½ 24 ∙ 25 = 300 (м )

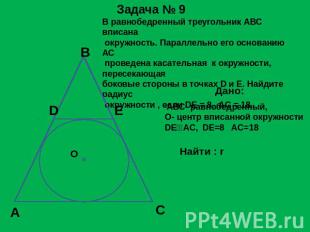
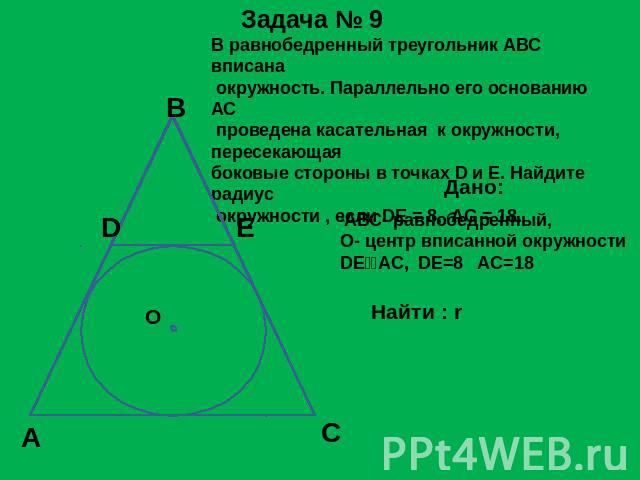
В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и E. Найдите радиус окружности , если DE = 8, AC = 18. АВС- равнобедренный,О- центр вписанной окружностиDEAC, DE=8 AC=18

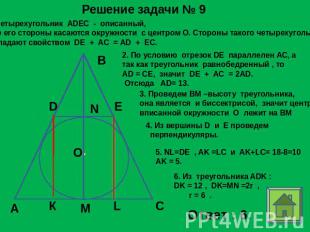
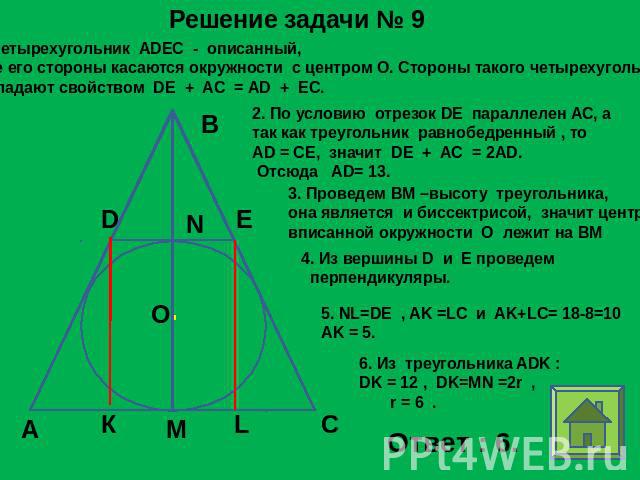
Решение задачи № 9 1.Четырехугольник ADEC - описанный, все его стороны касаются окружности с центром О. Стороны такого четырехугольникаобладают свойством DE + AC = AD + EC. 2. По условию отрезок DE параллелен АС, а так как треугольник равнобедренный , то AD = CE, значит DE + AC = 2AD. Отсюда AD= 13. 3. Проведем ВМ –высоту треугольника, она является и биссектрисой, значит центрвписанной окружности О лежит на ВМ 4. Из вершины D и Е проведем перпендикуляры. 5. NL=DE , AK =LC и AK+LC= 18-8=10AK = 5.

Исторические сведения. Треугольник - самая простая замкнутая прямолинейная фигура; одна из первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. В древней Греции учение о треугольниках развивалось в ионийской школе, основанной в VII в. до н. э. Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге «Начал» Евклида. Понятие о треугольнике исторически развивалось, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.

Справочный материал Проекция катета на гипотенузу- отрезок (часть гипотенузы) , соединяющий основание перпендикуляра , опущенного из прямого угла и конец катета, общий с гипотенузой. Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью Биссектрисой треугольника, проведенной из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая совпадает с центром описанной окружности. В равнобедренном треугольнике биссектриса, медиана и высота, проведенные к основанию, совпадают.

СПАСИБО ЗА ВНИМАНИЕ!