Презентация на тему: Треугольник простейший и неисчерпаемый

ТРЕУГОЛЬНИК простейший и неисчерпаемый Учитель информатики Юркова Т.Я.

Немного истории Древнегреческий историк Геродот оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – «землемерие» (от греч. «гео» - «земля» и «метрео» - «измеряю»). Древние землемеры выполняли геометрические построения, измеряли длины и площади; астрологи рассчитывали расположение небесных светил – все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике. Знакомый всем треугольник по праву считается простейшей из фигур: любая плоская, т. е. простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником. Так же называют и заключенную внутри образовавшегося контура часть плоскости. МЕНЮ

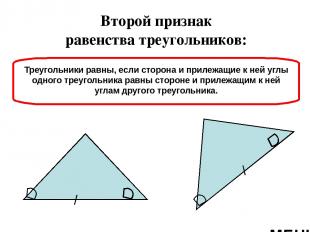
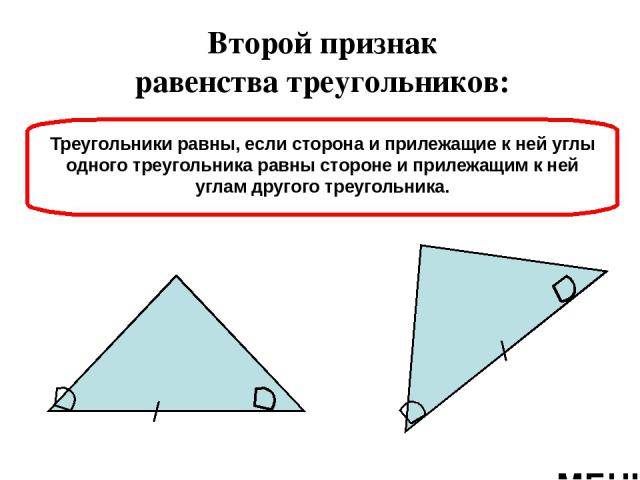
1 С 1 В 1 А С В А Второй признак равенства треугольников: Треугольники равны, если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника. МЕНЮ

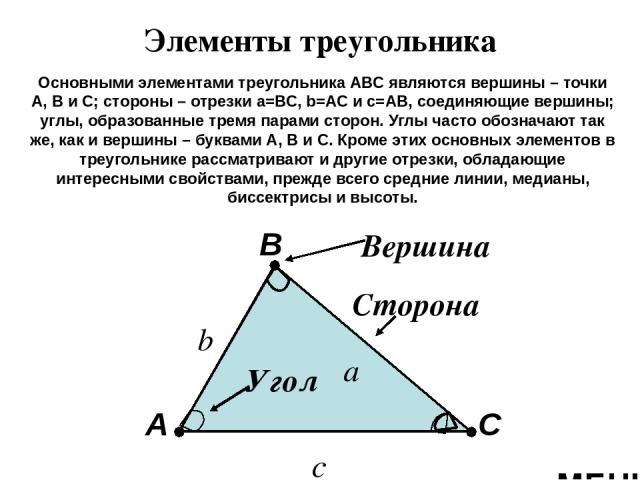
Элементы треугольника А В С Вершина Сторона Угол a b c Основными элементами треугольника АВС являются вершины – точки А, В и С; стороны – отрезки a=ВС, b=АС и c=АВ, соединяющие вершины; углы, образованные тремя парами сторон. Углы часто обозначают так же, как и вершины – буквами А, В и С. Кроме этих основных элементов в треугольнике рассматривают и другие отрезки, обладающие интересными свойствами, прежде всего средние линии, медианы, биссектрисы и высоты. МЕНЮ

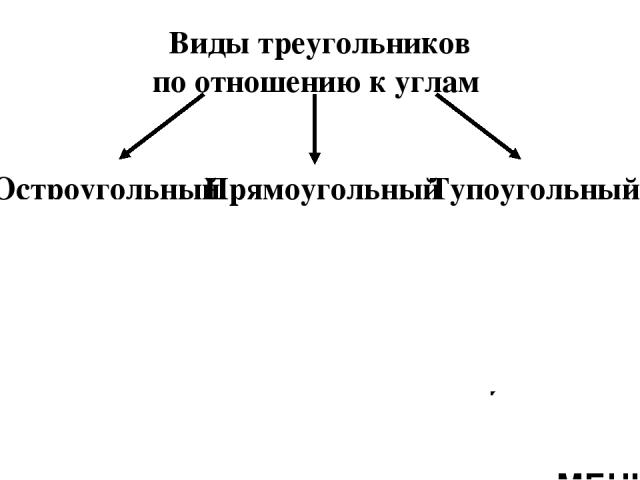
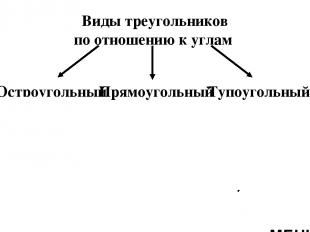
Виды треугольников по отношению к углам Остроугольный Прямоугольный Тупоугольный >90° 90° МЕНЮ

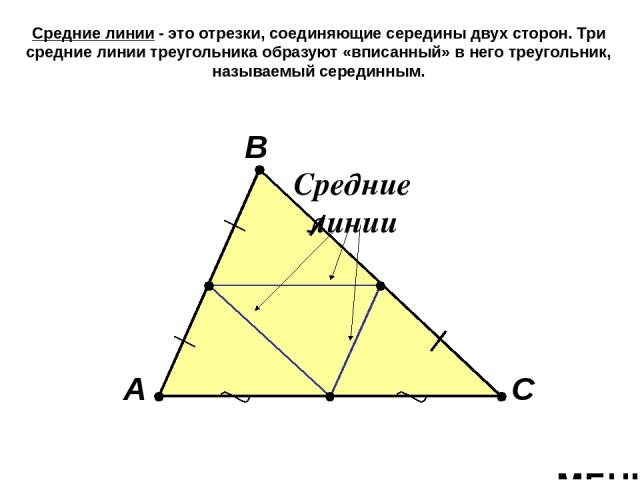
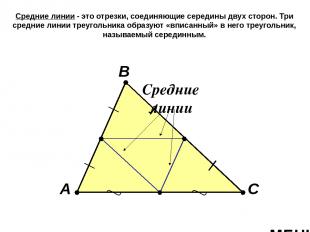
Средние линии - это отрезки, соединяющие середины двух сторон. Три средние линии треугольника образуют «вписанный» в него треугольник, называемый серединным. А В С Средние линии МЕНЮ

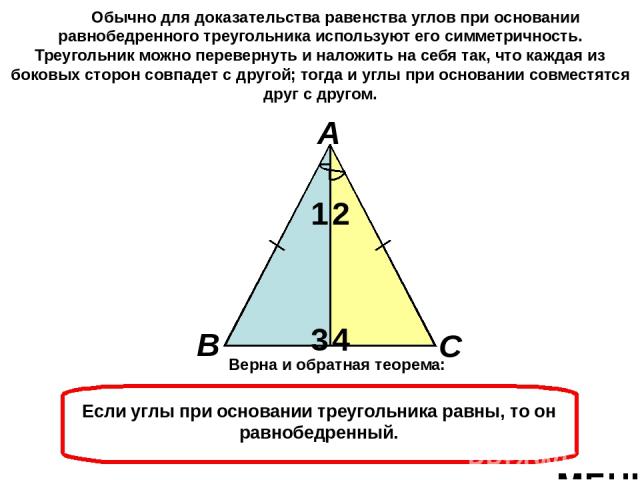
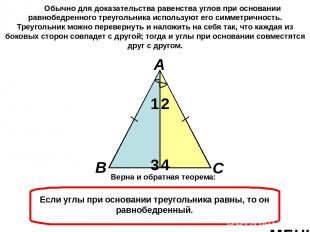
В одной из первых теорем «Начал» Евклида сформулировано основное свойство равнобедренного треугольника: углы при его основании равны. Доказательство этой теоремы приписывают Фалесу Милетскому, жившему за два века до Евклида. Впоследствии теорема получила название Pons asinorum, что на латыни означает «мост ослов». Объясняют такое название, с одной стороны, тем, что чертеж, использованный Евклидом для ее доказательства, напоминает мостик, а с другой – мнением, будто только ослы не могут этот мостик перейти. (Впрочем, в современном английском языке латинское выражение «pons asinorum» употребляется в несколько ином смысле – как «суровое испытание способностей неопытного человека».) Равнобедренный треугольник МЕНЮ

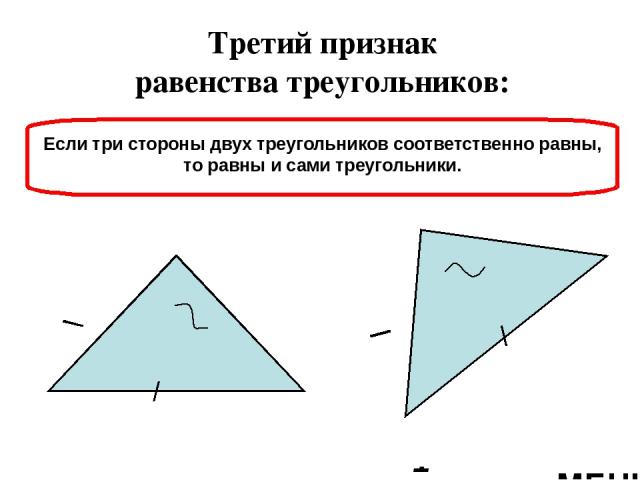
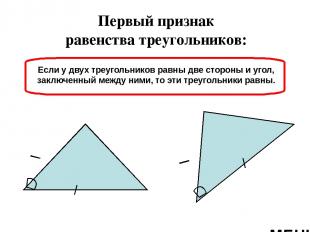
Признаки равенства треугольников: Первый признак равенства треугольников Второй признак равенства треугольников Третий признак равенства треугольников МЕНЮ

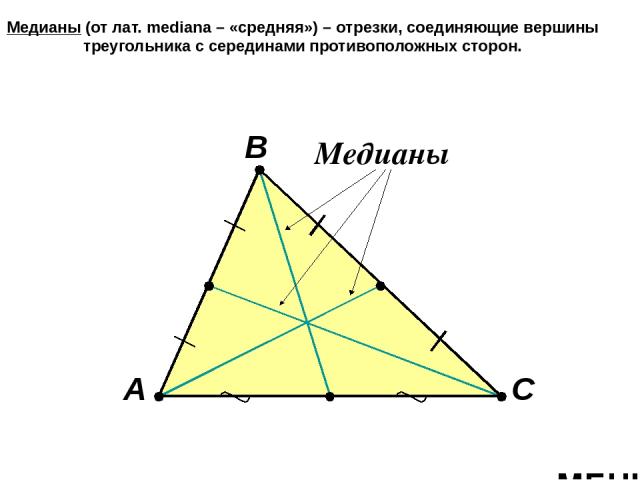
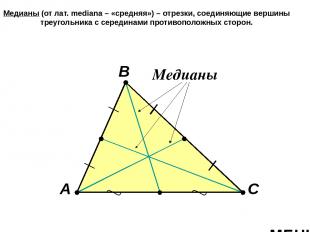
Медианы (от лат. mediana – «средняя») – отрезки, соединяющие вершины треугольника с серединами противоположных сторон. А В С Медианы МЕНЮ

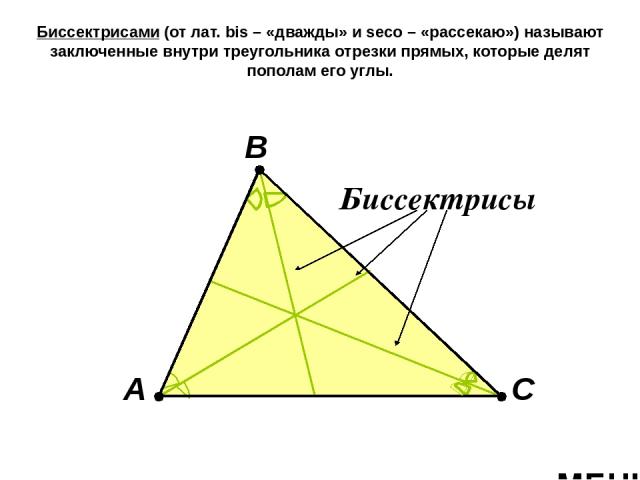
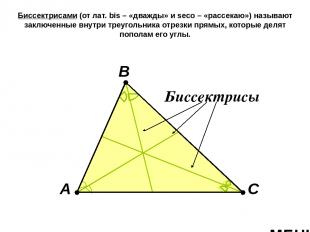
Биссектрисами (от лат. bis – «дважды» и seco – «рассекаю») называют заключенные внутри треугольника отрезки прямых, которые делят пополам его углы. А В С Биссектрисы МЕНЮ

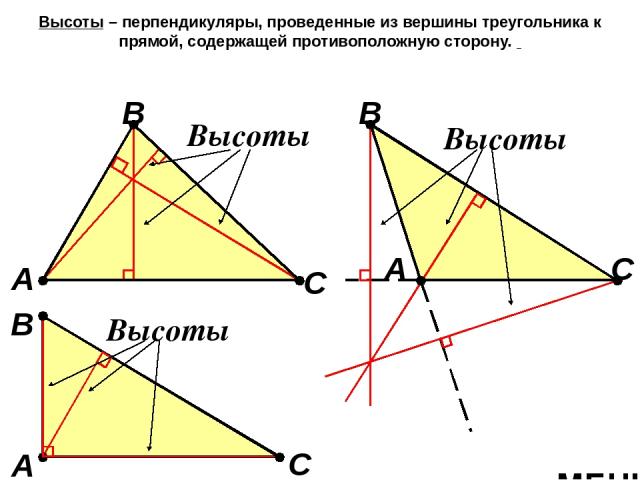
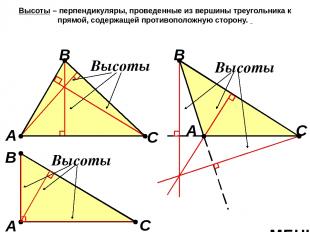
Высоты – перпендикуляры, проведенные из вершины треугольника к прямой, содержащей противоположную сторону. А В С Высоты А В С Высоты МЕНЮ А В С Высоты

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Справедливо и утверждение, обратное теореме Пифагора: Если стороны треугольника удовлетворяют равенству a² + b² = c², то этот треугольник прямоугольный. Теорема Пифагора b c a МЕНЮ

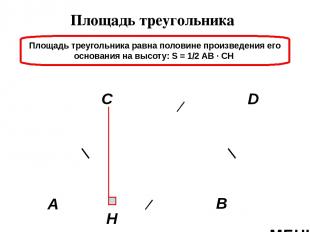
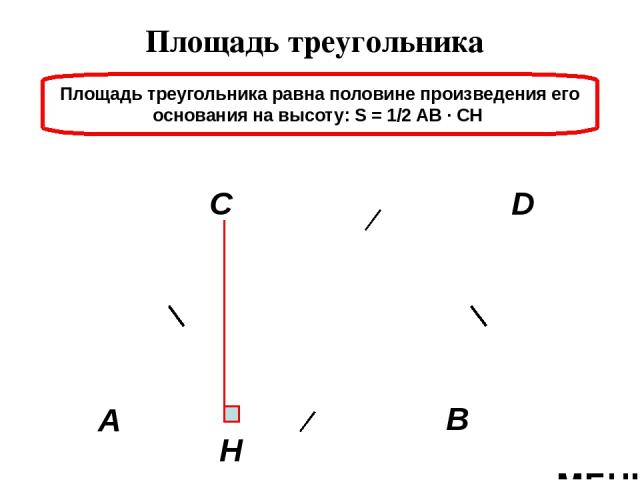
Площадь треугольника Площадь треугольника равна половине произведения его основания на высоту: S = 1/2 AB ∙ CH А В С Н D МЕНЮ

ПРОВЕРЬ СЕБЯ !!! ТЕСТ №1 МЕНЮ