Презентация на тему: Трансцендентные кривые

Федеральное государственное образовательное учреждение среднего профессионального образования «Димитровградский технический колледж»Проектпо теме: «Трансцендентные кривые»Выполнил: Семенов АлексейРуководитель: Кузьмина В.В.

Содержание Класс трансцендентных кривых Определение трансцендентной кривой Квадратриса Трактриса Цепная линия Циклоида Архимедова спираль Гиперболическая спираль Логарифмическая спираль Спираль Корню, клотоидаТрохоидаГипоциклоида Эпициклоида

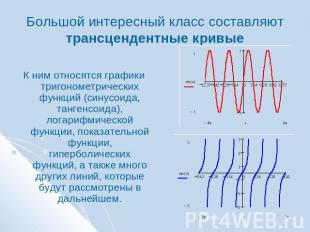
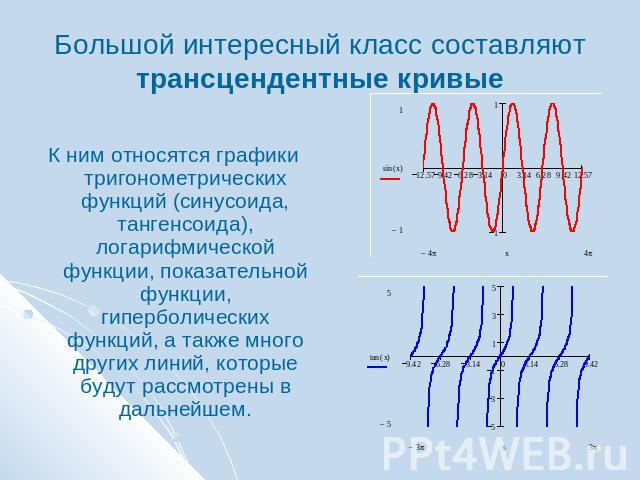
Большой интересный класс составляют трансцендентные кривые К ним относятся графики тригонометрических функций (синусоида, тангенсоида), логарифмической функции, показательной функции, гиперболических функций, а также много других линий, которые будут рассмотрены в дальнейшем.

Трансцендентная кривая Логарифмическая спираль Логарифмическая спираль Трансцендентная кривая - это кривая, уравнение которой в декартовой системе координат не является алгебраическим( в других системах координат может быть алгебраическим.)

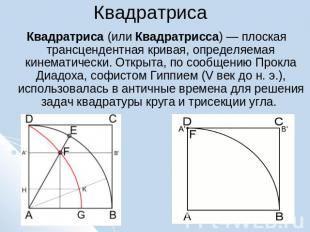
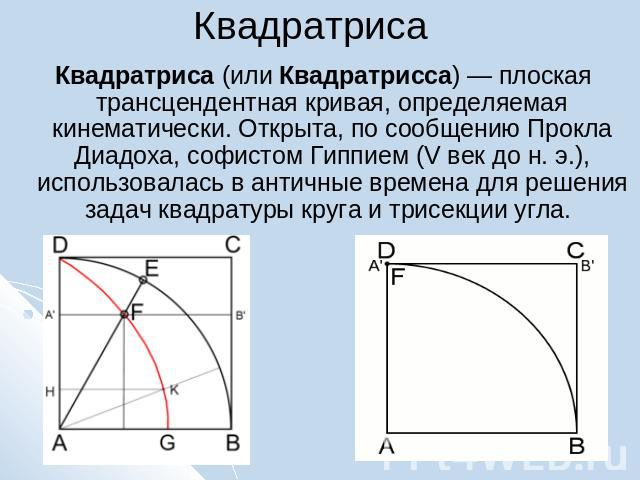
Квадратриса Квадратриса (или Квадратрисса) — плоская трансцендентная кривая, определяемая кинематически. Открыта, по сообщению Прокла Диадоха, софистом Гиппием (V век до н. э.), использовалась в античные времена для решения задач квадратуры круга и трисекции угла.

Уравнения В прямоугольных координатах можно записать уравнение квадратрисы в следующем виде:

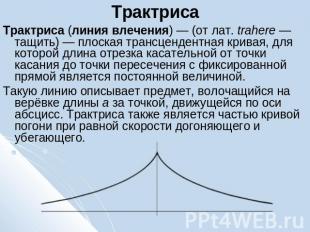
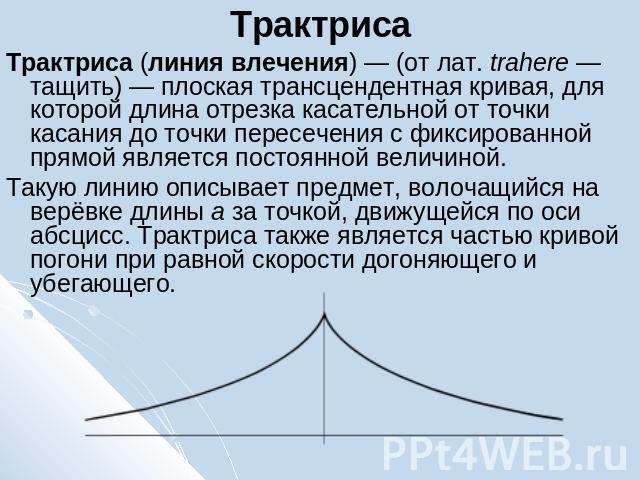
Трактриса Трактриса (линия влечения) — (от лат. trahere — тащить) — плоская трансцендентная кривая, для которой длина отрезка касательной от точки касания до точки пересечения с фиксированной прямой является постоянной величиной.Такую линию описывает предмет, волочащийся на верёвке длины a за точкой, движущейся по оси абсцисс. Трактриса также является частью кривой погони при равной скорости догоняющего и убегающего.

УравненияПараметрическое описание: Уравнение в декартовых координатах:

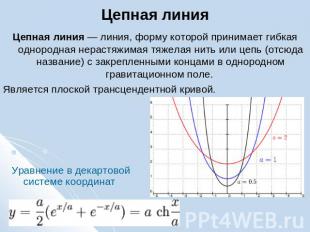
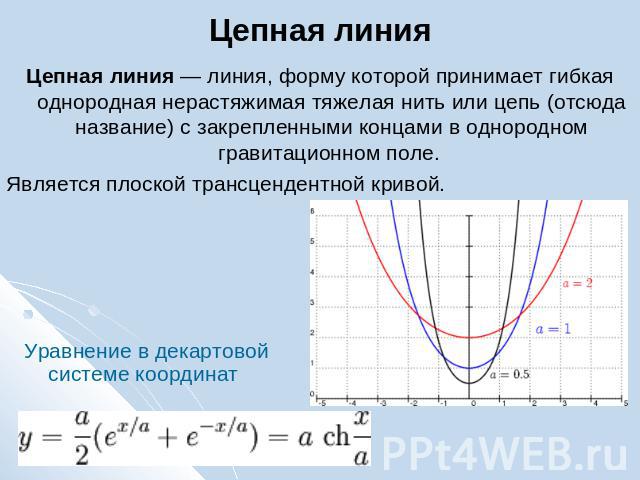
Цепная линия Цепная линия — линия, форму которой принимает гибкая однородная нерастяжимая тяжелая нить или цепь (отсюда название) с закрепленными концами в однородном гравитационном поле. Является плоской трансцендентной кривой. Уравнение в декартовой системе координат

Краткая историческая справка Поверхность, образованная вращением дуги цепной линии вокруг оси Оx, называется катеноидом.Цепные линии используются в расчетах, связанных с провисанием проводов, тросов и т.п. Форму кривой провисания впервые рассматривал Г. Галилей (1638), который считал ее параболой. Истинная форма кривой найдена Г. Лейбницем, Я. и И. Бернулли, Х. Гюйгенсом.Х. Гюйгенс предложил термин «Цепная линия»

Применение АркиПеревёрнутая цепная линия — идеальная форма для арок. Однородная арка в форме перевёрнутой цепной линии испытывает только деформации сжатия, но не излома.МостыГорбатый мост имеет форму, близкую к цепной линии.Стоит заметить, что цепь подвесного моста имеет форму параболы, а не цепной линии. Это связано с тем, что пролёт моста намного тяжелее цепи.

ЦИКЛОИДА Циклоида (от греч.— круглый) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся без скольжения по прямой.

Уравнения Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r. Циклоида описывается параметрическими уравнениями: Уравнение в декартовых координатах: Циклоида может быть получена как решение дифференциального уравнения:

У циклоиды масса любопытнейших свойств. Оказывается, например, что циклоида является кривой наибыстрейшего спуска. Иначе говоря, скатываясь по снежной горке, профиль которой выполнен в виде циклоиды, мы окажемся у основания горки быстрее, чем в случае другой формы горки. Траектория конца маятника, как и ограничивающие его боковые "щеки", представляют из себя циклоиду

Архимедова спираль Архимедова спираль — плоская кривая, траектория точки M (см Рис. 1), которая равномерно движется вдоль луча OV с началом в O, в то время как сам луч OV равномерно вращается вокруг O. Другими словами, расстояние ρ = OM пропорционально углу поворота φ луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.

Вычисление длины дуги Архимедовой спирали Бесконечно малый отрезок дуги dl равен (см. Рис.): ,где dρ — приращение радиуса ρ, при приращении угла φ на dφ. Для бесконечно малого приращения угла dφ, справедливо: .Поэтому: так как ρ = kφ иdρ = kdφили .Длина дуги L равна интегралу от dl по dφ в пределах от 0 до φ: .

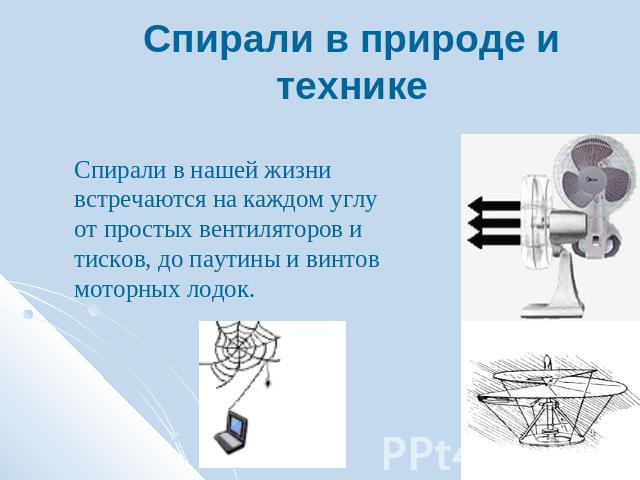
Спирали в природе и технике Спирали в нашей жизни встречаются на каждом углу от простых вентиляторов и тисков, до паутины и винтов моторных лодок.

Спирали в природе и технике

Спирали в природе и технике

Спиральные галактики

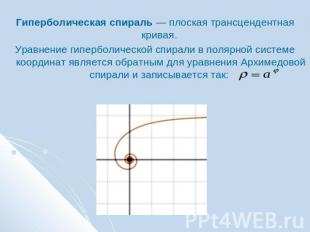
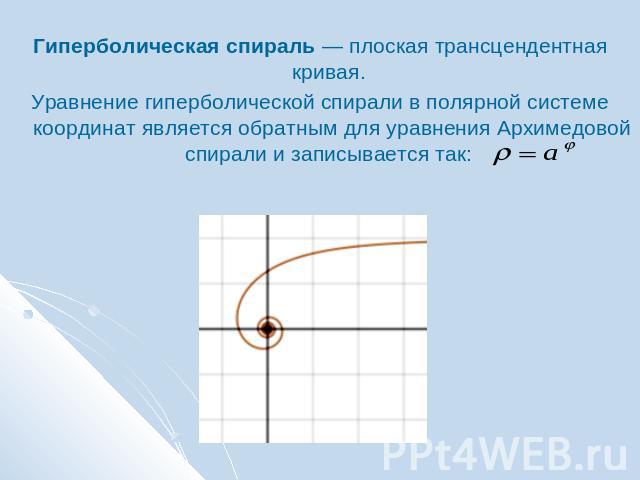
Гиперболическая спираль — плоская трансцендентная кривая. Уравнение гиперболической спирали в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так:

Уравнение гиперболической спирали в декартовых координатах:Параметрическая запись уравнения: Спираль имеет асимптоту y = a: при t стремящемся к нулю ордината стремится к a, а абсцисса уходит в бесконечность:

ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ - плоская трансцендентная кривая, пересекающая все радиусы-векторы под одним и тем же углом (рис.1). Уравнение в полярных координатах:При a > 1 и логарифмическаяспираль развертывается против хода часовой стрелки, при спираль закручивается по ходу часовой стрелки, стремясь к своей асимптотической точке O. Если a < 1, логарифмическая спираль закручивается против хода часовой стрелки.

Логарифмическая спираль относится к псевдоспиралям. Логарифмическая спираль переходит в себя при линейных преобразованиях плоскости: её Эволюта, подера – также логарифмическая спираль. При стереографической проекции плоскости на сферу логарифмическая спираль переходит в локсодромию. Логарифмическая спираль широко используется в технике:

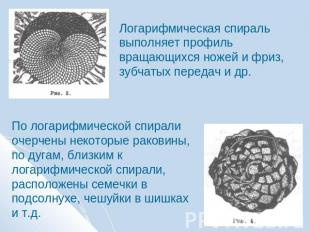
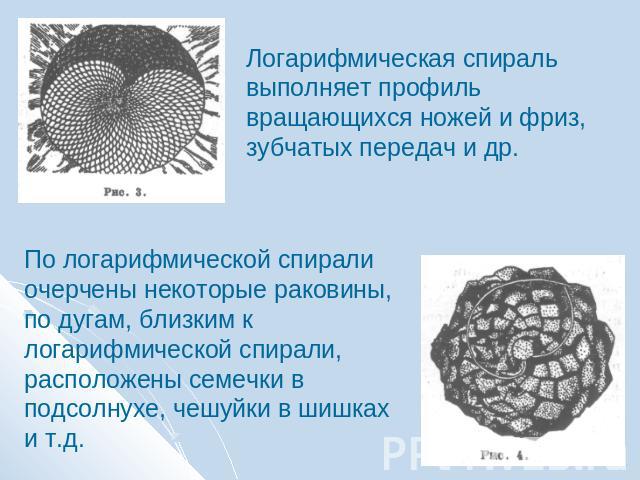
Логарифмическая спираль выполняет профиль вращающихся ножей и фриз, зубчатых передач и др. По логарифмической спирали очерчены некоторые раковины, по дугам, близким к логарифмической спирали, расположены семечки в подсолнухе, чешуйки в шишках и т.д.

Клотоида или Спираль Корню — кривая, у которой кривизна изменяется линейно как функция длины дуги. Она используется как переходная дуга в дорожном строительстве. Когда участок дороги имеет форму клотоиды, руль поворачивается равномерно. Такая форма дороги позволяет преодолевать поворот без существенного снижения скорости. Клотоида применялась Корню для облегчения расчёта дифракции в прикладных задачах.

Описывается параметрическими уравнениями где , где R — радиус неподвижной окружности, r — радиус катящейся окружности.Модуль величины k определяет форму гипоциклоиды. При k = 2 гипоциклоида представляет собой диаметр неподвижной окружности, при k = 4 является астроидой.

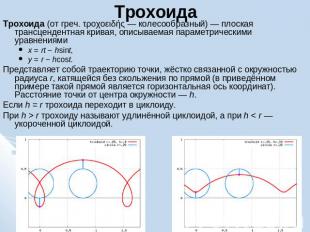
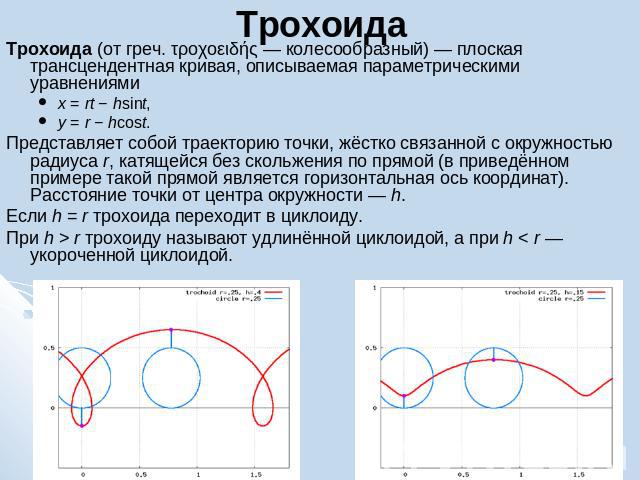
Трохоида Трохоида (от греч. τροχοειδής — колесообразный) — плоская трансцендентная кривая, описываемая параметрическими уравнениямиx = rt − hsint,y = r − hcost.Представляет собой траекторию точки, жёстко связанной с окружностью радиуса r, катящейся без скольжения по прямой (в приведённом примере такой прямой является горизонтальная ось координат). Расстояние точки от центра окружности — h.Если h = r трохоида переходит в циклоиду.При h > r трохоиду называют удлинённой циклоидой, а при h < r — укороченной циклоидой.

Гипоциклоида Гипоциклоида (от греческих слов ὑπό — под, внизу и κύκλος — круг, окружность) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.

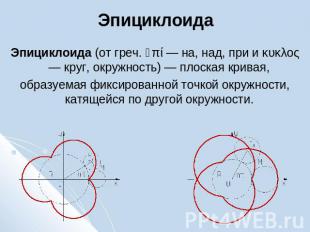
Эпициклоида Эпициклоида (от греч. ὲπί — на, над, при и κυκλος — круг, окружность) — плоская кривая, образуемая фиксированной точкой окружности, катящейся по другой окружности.

Уравнения Если центр неподвижной окружности находится в начале координат, её радиус равен R, радиус катящейся по ней окружности равен r, то эпициклоида описывается параметрическими уравнениями относительно : где α — угол поворота эпициклоиды относительно центра неподвижной окружности, — параметр, но фактически это угол наклона отрезка между центрами к оси OX. Можно ввести величину , тогда уравнения предстанут в виде

Применение Последнее уравнение выражает такое кинематическое свойство эпициклоиды: если дуга обычной эпициклоиды перекатывается без скольжения по прямой, то центр кривизны точки касания двигается по эллипсу; центр эллипса лежит в той точке прямой, через которую перекатывается вершина эпициклоиды.

Информационные источники Литература1. Большой энциклопедический словарь «Математика»,Гл. редактор Ю.В. Прохоров, Научное изд-во «Большая Российская Энциклопедия», М.: 19982. Д.В. Клетеник Сборник задач по аналитической геометрии под ред. проф. Н.В.Ефимова, Государственное изд-во физико-математической литературы, М.: 19603. Математическая энциклопедия. Главный редактор И.М. Виноградов, т.3 – М.: «Советская энциклопедия», 1982Интернет ресурсы: www.college.ru www.gee.ru