Презентация на тему: Основные фигуры в пространстве

Основные фигуры в пространстве

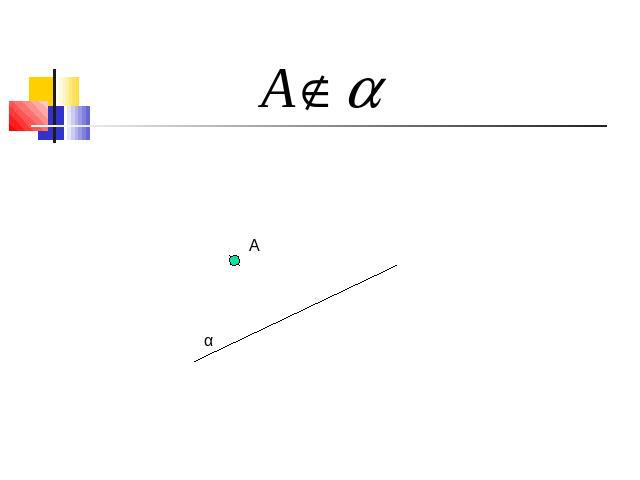
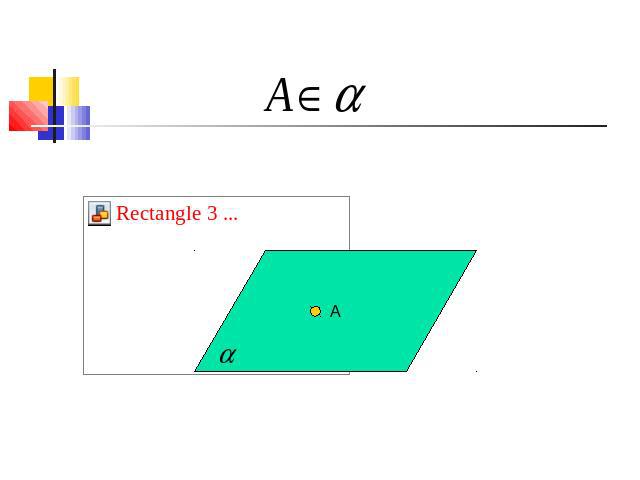
Точка Прописные латинские буквы A, B, C, D, E, K, …

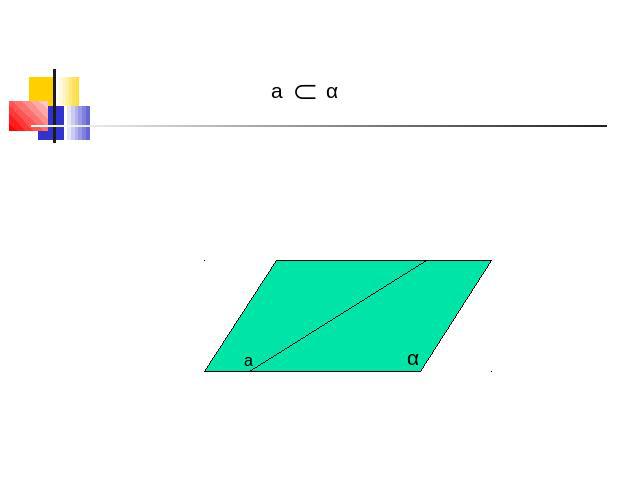
Прямая Строчные латинские буквы a, b, c, d, e, k, …

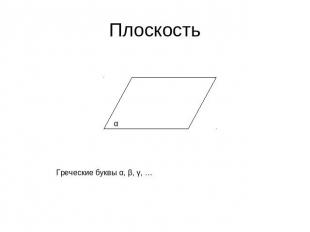
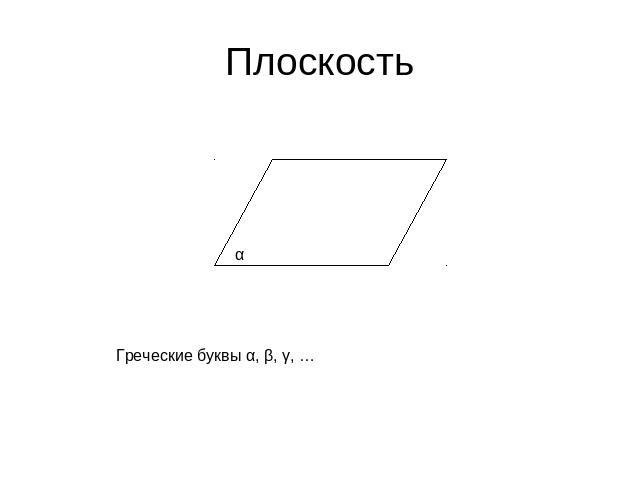
Плоскость Греческие буквы α, β, γ, …

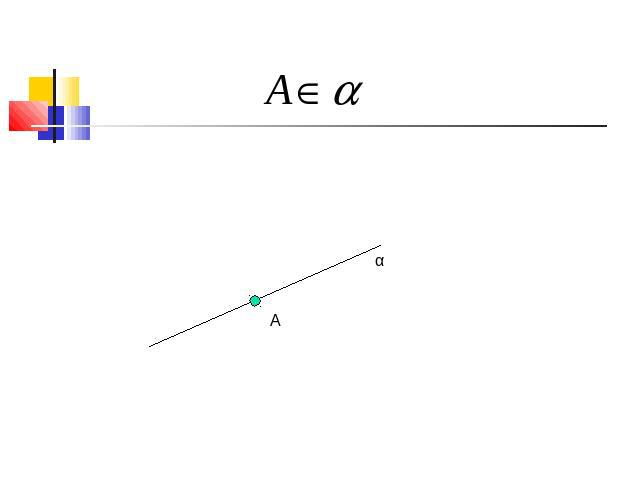
Взаимное расположение точек, прямых, плоскостей в пространстве.

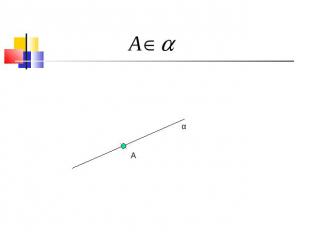
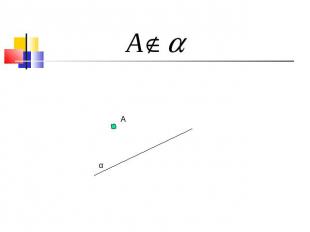
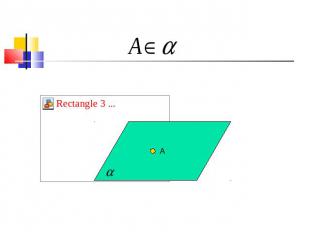
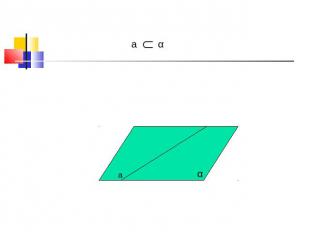
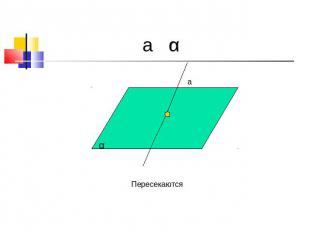
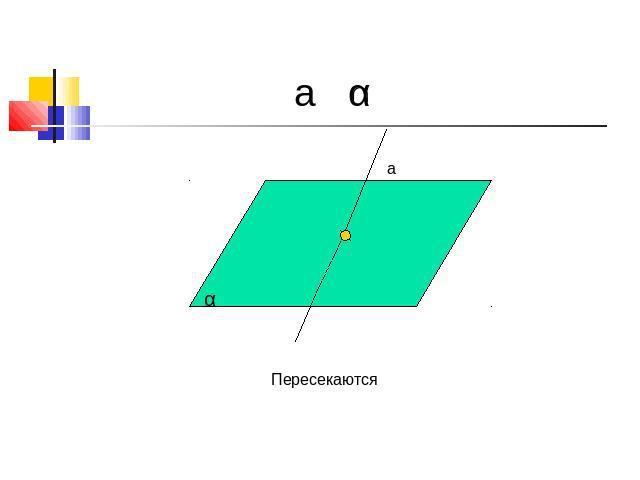
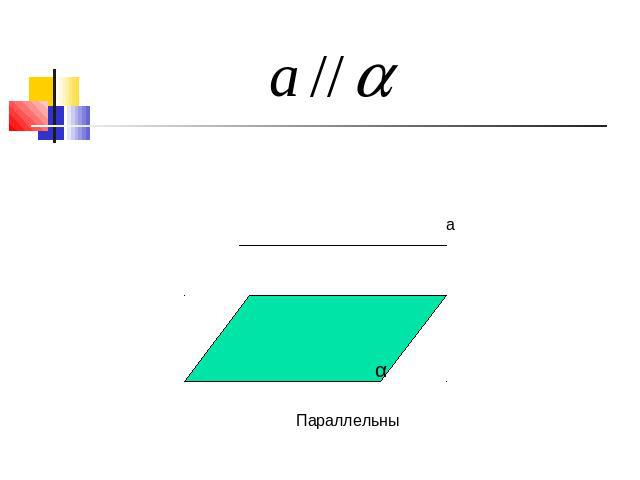
a α

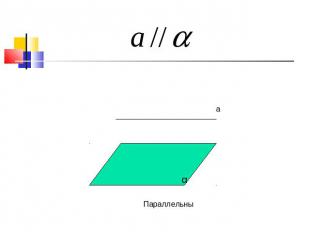
Параллельны

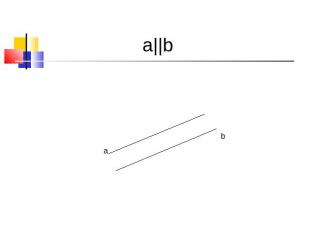
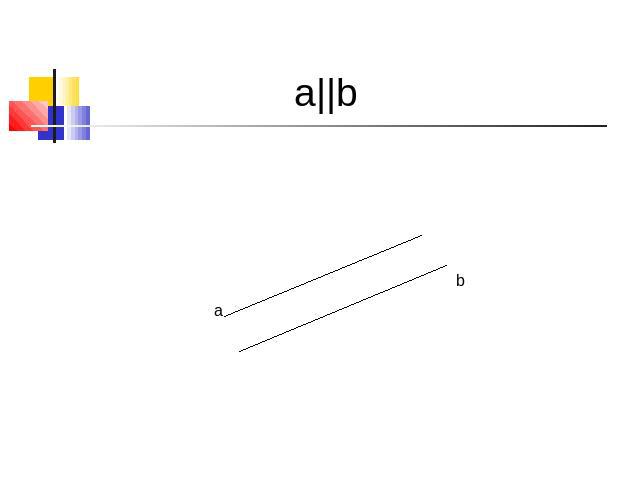
a||b

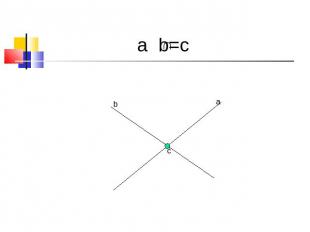
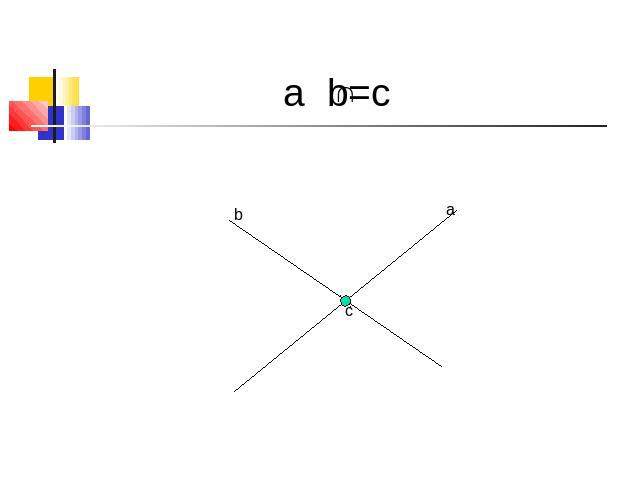
a b=c

Параллельны

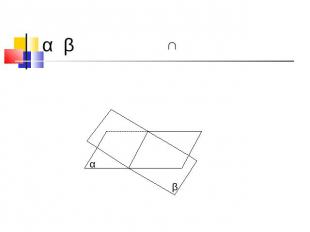
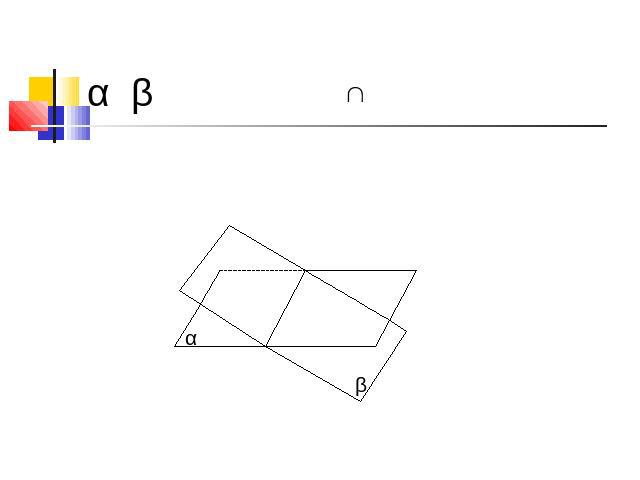
α β

Аксиомы стереометрии

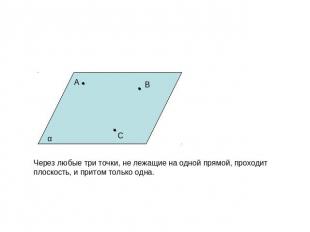
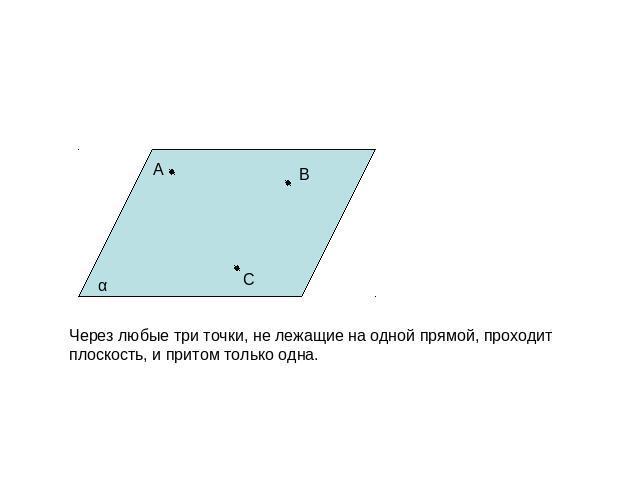
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

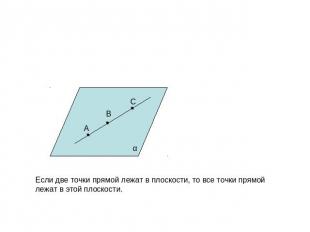
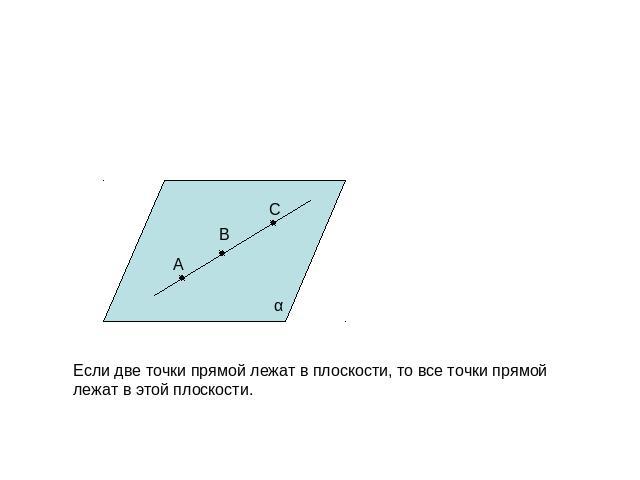
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

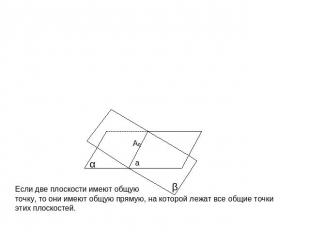
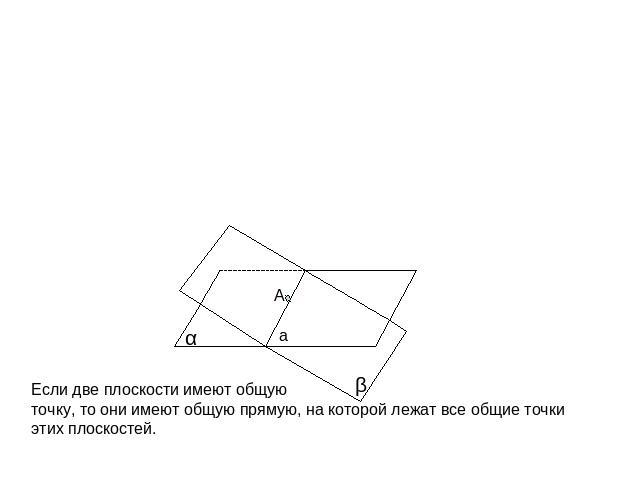
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точкиэтих плоскостей.

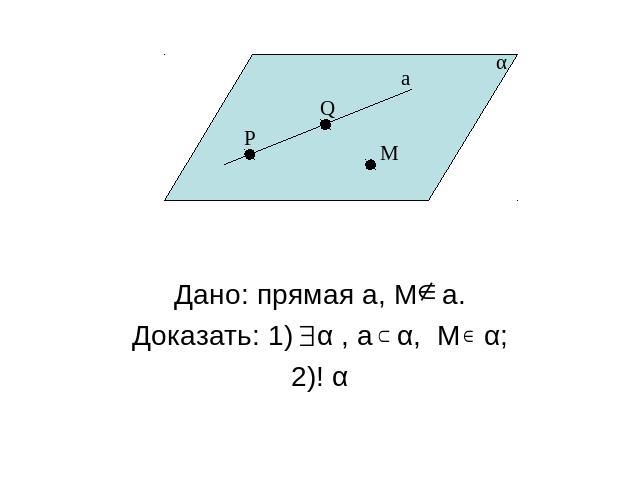
Следствия из аксиом стереометрии. Теорема 1.Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

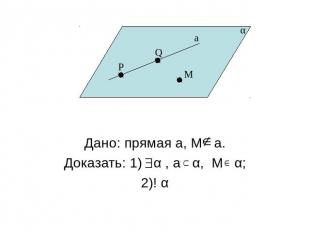
Дано: прямая а, М a.Доказать: 1) α , а α, М α;2)! α

Доказательство. Возьмем точки Р a, Q a.По А1 α, Р α,Q α, М α. Так как Р α и Q α, то по А2 а α. Любая плоскость, проходящая через прямую а и точку М, проходит через точки М, P, Q. Следовательно, она совпадает с α, так как по А1 через точки M, P,Q проходит только одна плоскость.

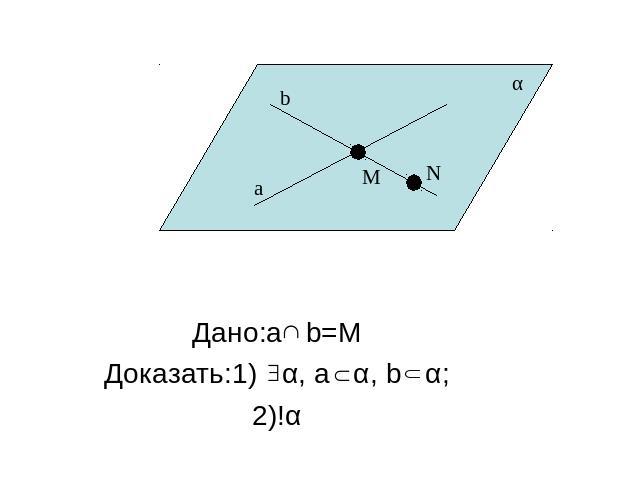
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

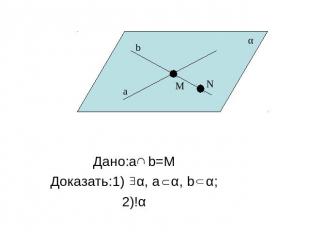
Дано:a b=MДоказать:1) α, а α, b α;2)!α

Доказательство Возьмем точку N b. По Т1 α, а α,N α. Так как N b,M b и N α, М α,то по А2 b α. Итак, a α и b α. Любая плоскость, проходящая через a и b, проходит через N. Следовательно, она совпадает с α, так как по T1 через N и a проходит только одна плоскость.

Способы задания плоскости в пространстве

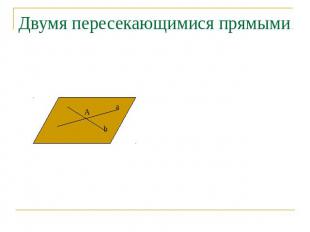
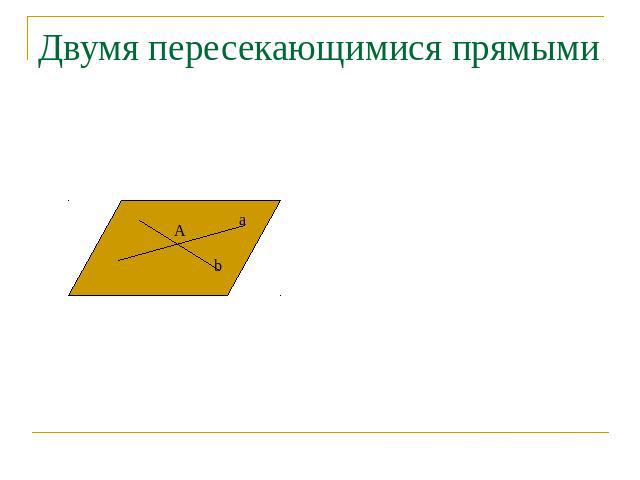
Двумя пересекающимися прямыми

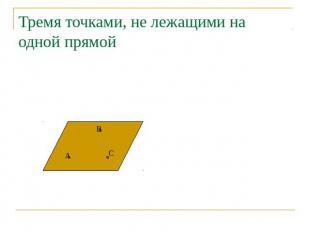
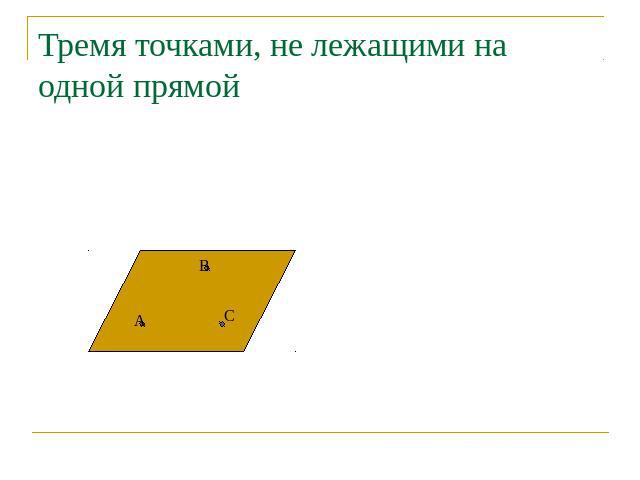
Тремя точками, не лежащими на одной прямой

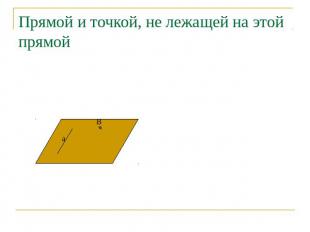
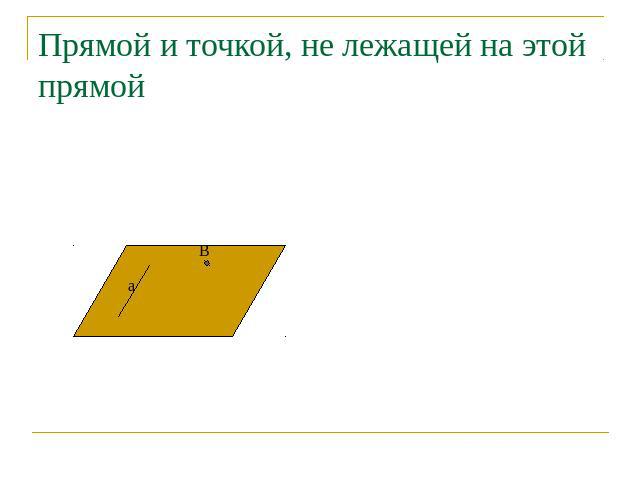
Прямой и точкой, не лежащей на этой прямой

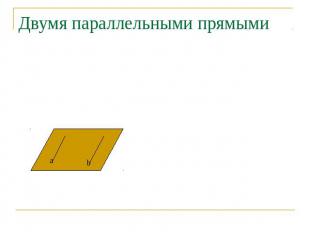
Двумя параллельными прямыми

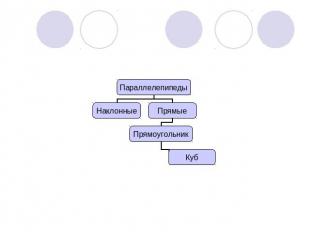
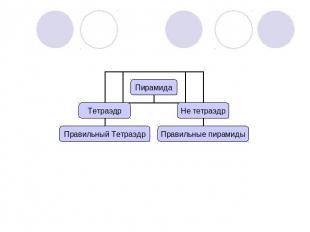
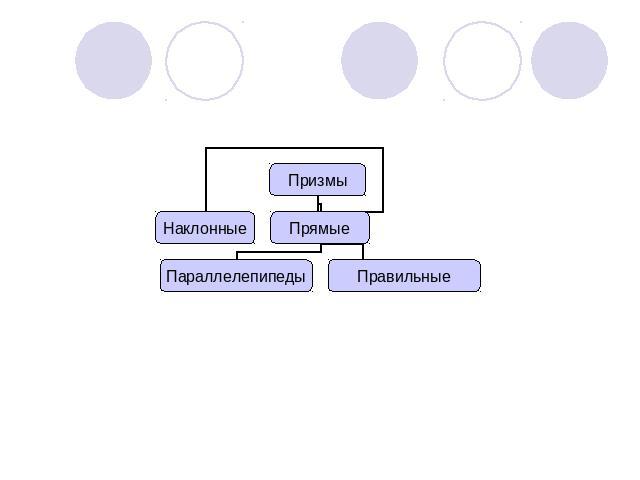
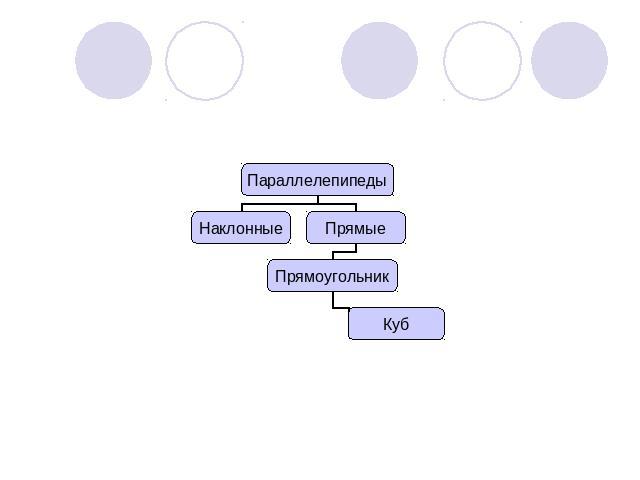
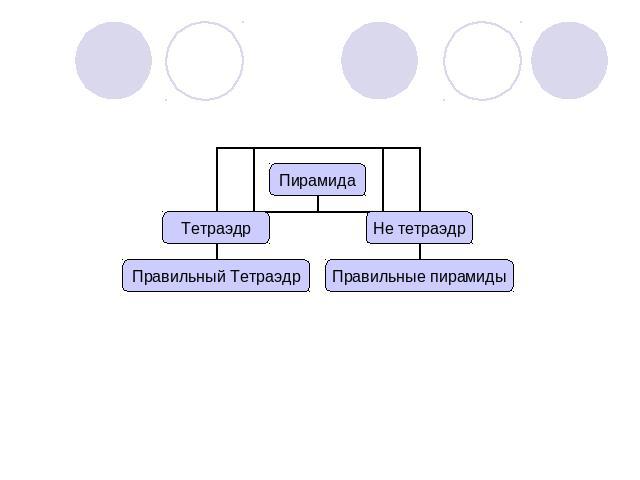
Многогранники. Тела вращения.