Презентация на тему: Теорема Фалеса

Теорема ФАЛЕСА Геометрия 8
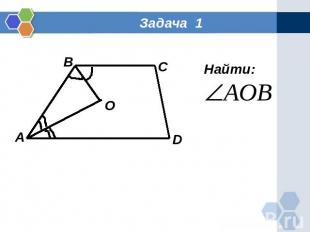
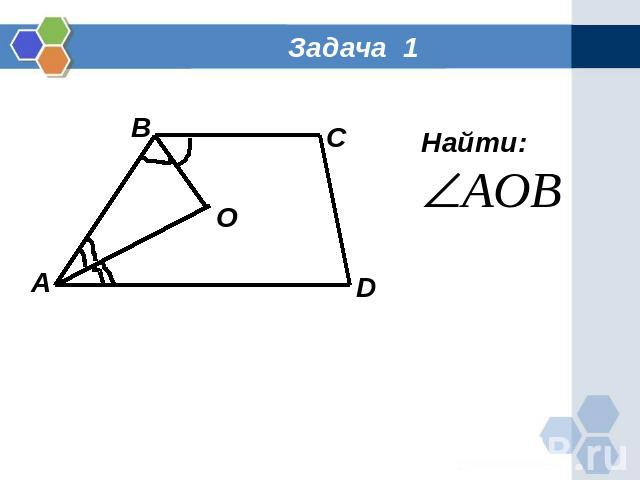
Задача 1 Найти:
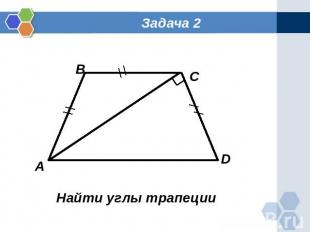
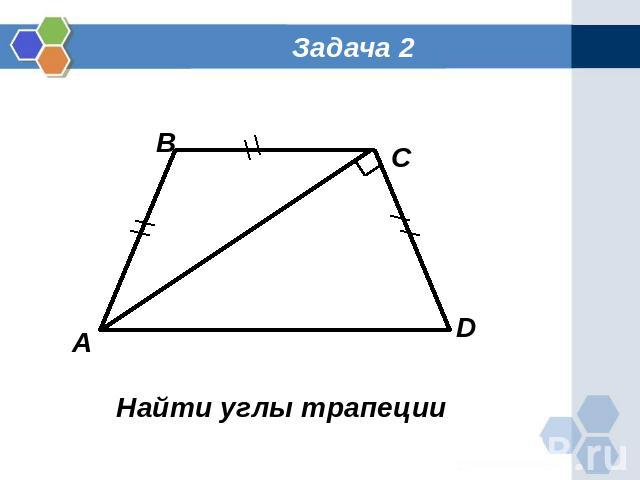
Задача 2 Найти углы трапеции
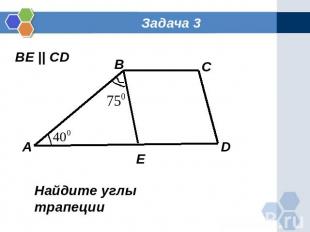
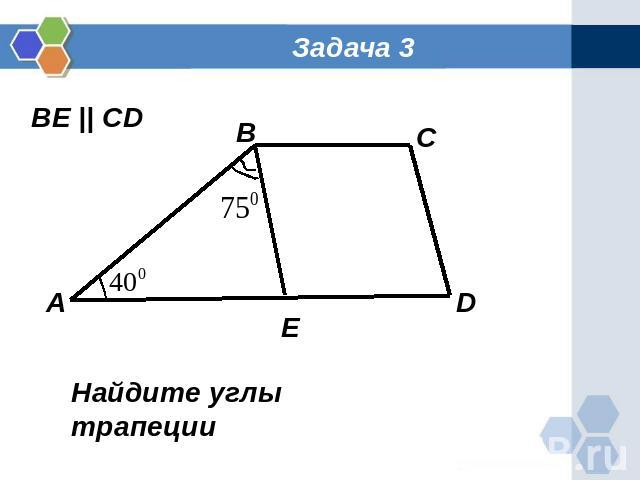
Задача 3 Найдите углы трапеции
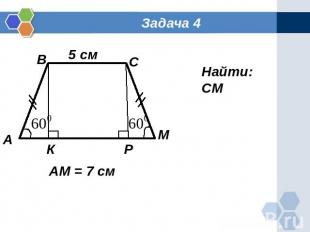
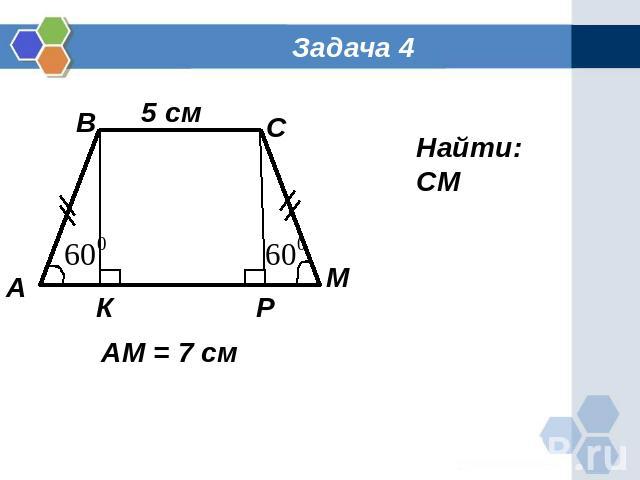
Задача 4 Найти: СМ
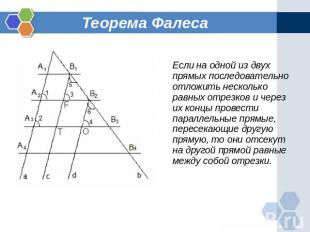
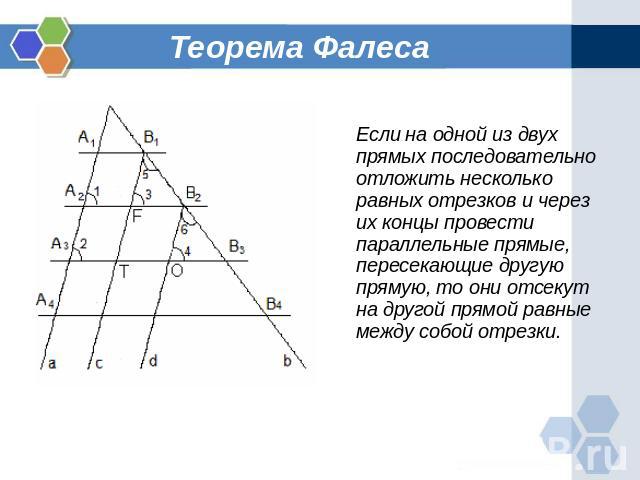
Теорема Фалеса Если на одной из двух прямых последовательно отложить несколько равных отрезков и через их концы провести параллельные прямые, пересекающие другую прямую, то они отсекут на другой прямой равные между собой отрезки.
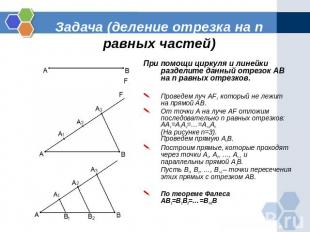
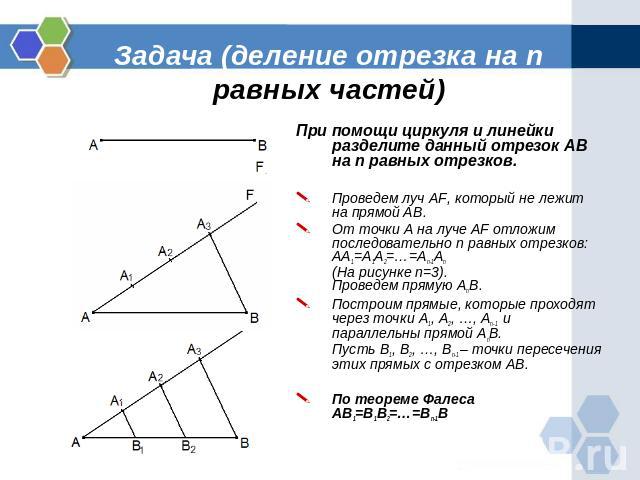
Задача (деление отрезка на n равных частей) При помощи циркуля и линейки разделите данный отрезок AB на n равных отрезков.Проведем луч AF, который не лежит на прямой AB.От точки A на луче AF отложим последовательно n равных отрезков: AA1=A1A2=…=An-1An (На рисунке n=3). Проведем прямую AnB.Построим прямые, которые проходят через точки A1, A2, …, An-1 и параллельны прямой AnВ.Пусть B1, B2, …, Bn-1 – точки пересечения этих прямых с отрезком AB.По теореме Фалеса AB1=B1B2=…=Bn-1B
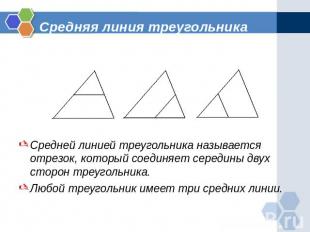
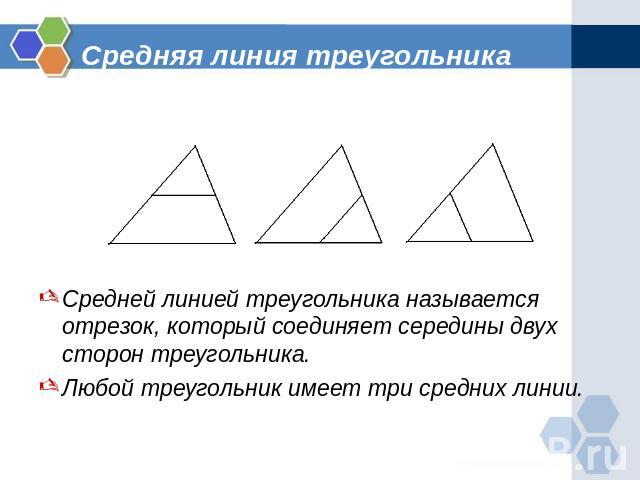
Средняя линия треугольника Средней линией треугольника называется отрезок, который соединяет середины двух сторон треугольника.Любой треугольник имеет три средних линии.

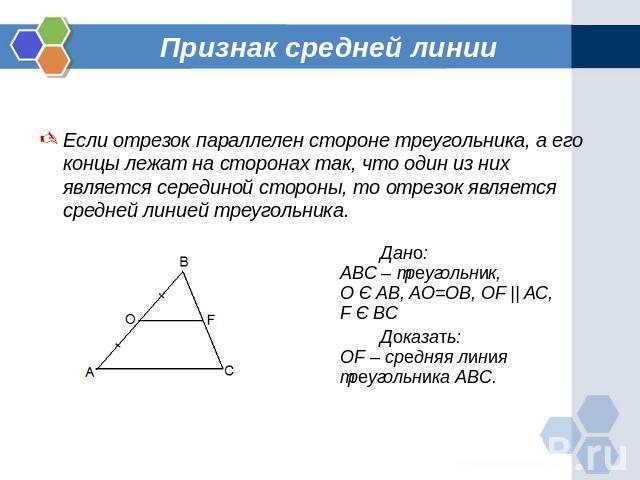
Признак средней линии Если отрезок параллелен стороне треугольника, а его концы лежат на сторонах так, что один из них является серединой стороны, то отрезок является средней линией треугольника.Дано:ABC – треугольник,О Є AB, AO=OB, OF || AC,F Є BCДоказать:OF – средняя линия треугольника ABC.
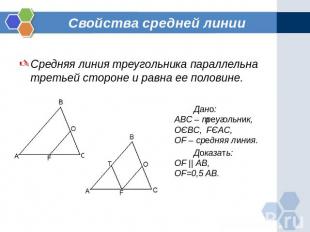
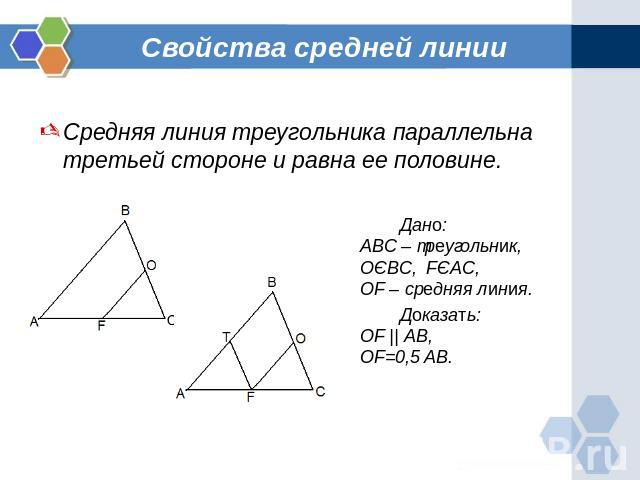
Свойства средней линии Средняя линия треугольника параллельна третьей стороне и равна ее половине.Дано:ABC – треугольник,ОЄBC, FЄAC,OF – средняя линия.Доказать:OF || AB,OF=0,5 AB.

Домашняя работа № 391, 392№ 385 выучить как теоремуПринести циркуль.