Презентация на тему: Пирамида

ПирамидаПодготовили : Асадова Ламия, Шимонаев Павел, Волкова Екатерина, Балыбин Артем, Олзоев Тимур

ОпределениеЭлементы пирамидыСвойства пирамидыПравильная пирамидаСвойства правильной пирамидыПрямоугольная пирамидаПоверхность пирамидыФормулы, связанные с пирамидой
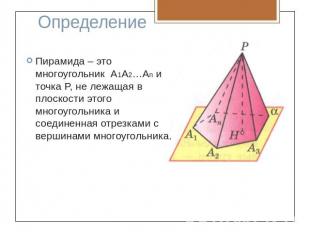
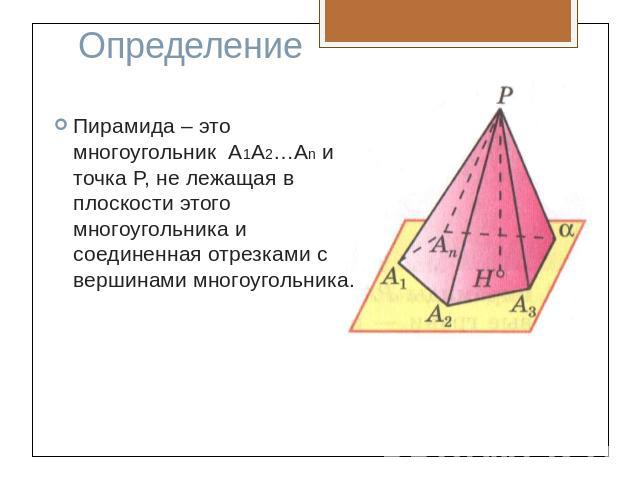
ОпределениеПирамида – это многоугольник А1А2…Аn и точка P, не лежащая в плоскости этого многоугольника и соединенная отрезками с вершинами многоугольника.
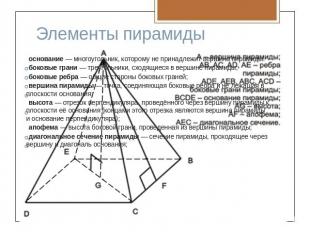
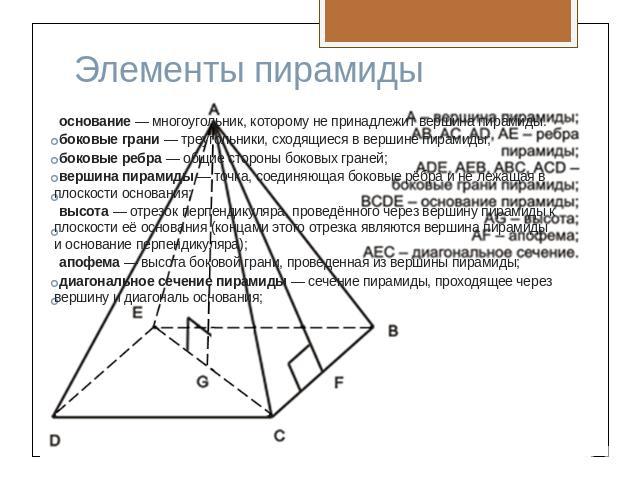
Элементы пирамиды основание — многоугольник, которому не принадлежит вершина пирамиды.боковые грани — треугольники, сходящиеся в вершине пирамиды;боковые ребра — общие стороны боковых граней;вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);апофема — высота боковой грани, проведенная из вершины пирамиды;диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;

Свойства пирамидыЕсли боковые грани наклонены к плоскости основания под одним углом, то : в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в ее центр;высоты боковых граней равны;

Свойства пирамиды Если все боковые ребра равны, то:около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;боковые ребра образуют с плоскостью основания равные углы.также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
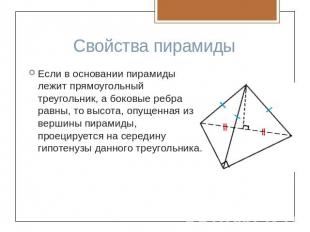
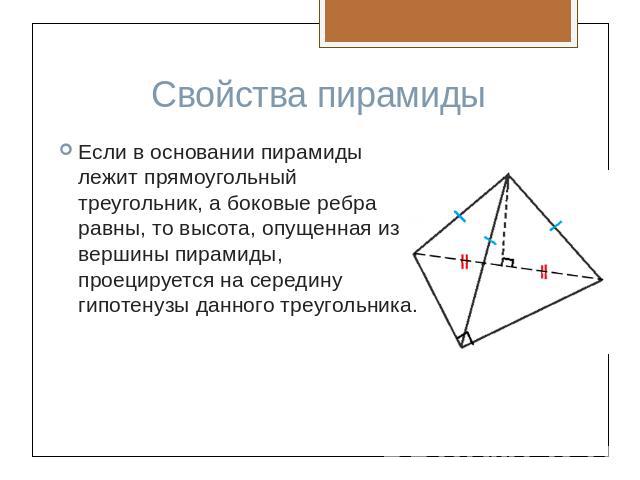
Свойства пирамидыЕсли в основании пирамиды лежит прямоугольный треугольник, а боковые ребра равны, то высота, опущенная из вершины пирамиды, проецируется на середину гипотенузы данного треугольника.

Правильная пирамидаПирамида называется правильной, если ее основанием является правильный многоугольник, а вершина проецируется в центр основания.
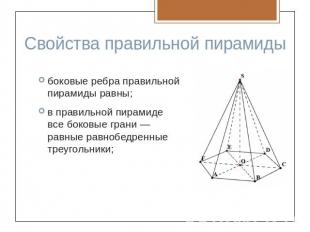
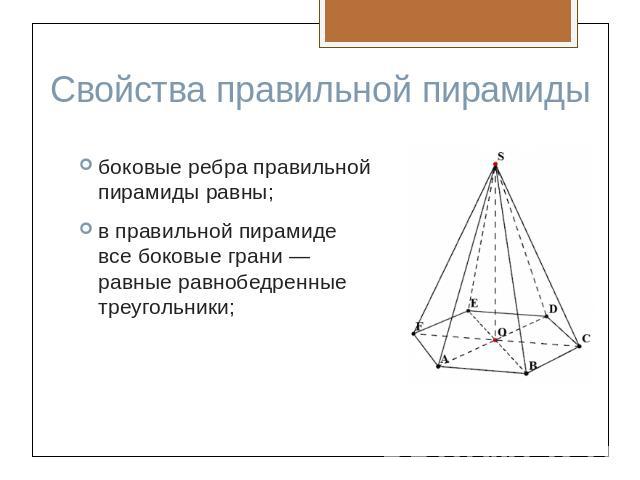
Свойства правильной пирамидыбоковые ребра правильной пирамиды равны;в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

Прямоугольная пирамидаПирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Поверхность пирамидыПлощадью полной поверхности пирамиды называется сумма площадей всех ее граней (т.е. основания и боковых граней).Площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.

Формулы, связанные с пирамидойЧтобы определить площадь боковой поверхности пирамиды, надо найти сумму площадей всех её боковых граней:

Формулы, связанные с пирамидой
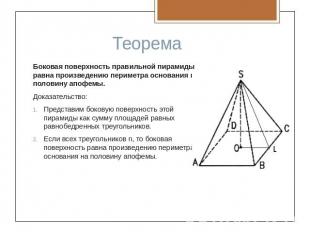
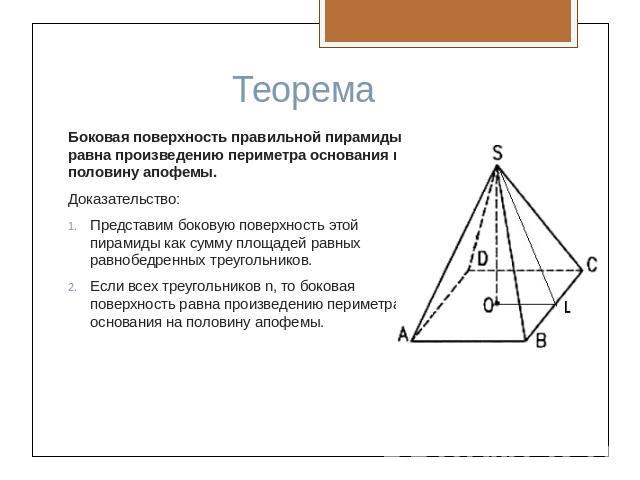
Боковая поверхность правильной пирамиды равна произведению периметра основания на половину апофемы.Доказательство:Представим боковую поверхность этой пирамиды как сумму площадей равных равнобедренных треугольников.Если всех треугольников n, то боковая поверхность равна произведению периметра основания на половину апофемы.

Формулы, связанные с пирамидой