Презентация на тему: Паркеты. Правильные, полуправильные

Паркеты. Правильные, полуправильные

Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.

Из каких правильных многоугольников можно составить паркет?

попытка №1 ура! получился!

попытка №2 , из пятиугольников увы. ничего не вышло...

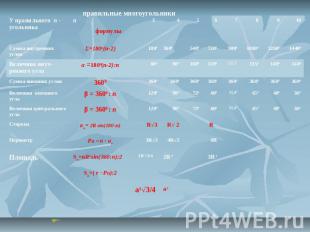
ПРАВИЛЬНЫЕ ПАРКЕТЫ

Необходимое усло-вие для построения паркета. в узле 360 градусов

теорема №1 Возле любого правильного многоугольника можно описать окружность . теорема№2 В окружность можно вписать правильный многоугольник.

m=3600:α 2.при n=4 ,то m=3600/900=4 четырёхугольника в узле 1. при n=3, то m=3600/600=6 треугольников в узле При п>7 внутренние углы правильных п-угольников больше 1200. Кроме того внутренние углы правильного многоугольника всегда меньше1800 .1200<α<1800 Из двух дробей с одинаковыми числителями та дробь больше, у которой знаменатель меньше. Поэтому, 3600/1200 > 3600/α > 3600/1800 , 2 < 3600/α <3, 2<т<3, Отсюда следует, что т =2,…. т.е. число не натуральное. Итак, для п >7 не существует правильных многоугольников для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников построить нельзя!

например: Из правильных пятиугольников нельзя сложить паркет.

вывод: Только из этих правильных многоугольников можно построить правильный паркет.

паркет из правильных шестиугольников

ПОЛУПРАВИЛЬНЫЕ ПАРКЕТЫ

Необходимое условие для построения паркета. В УЗЛЕ 360 ГРАДУСОВ

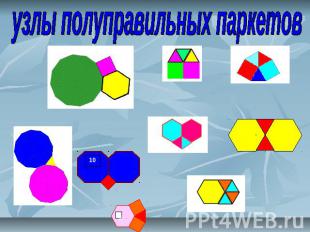
узлы полуправильных паркетов

полуправильный паркет вывод: полуправильных паркетов получается видов

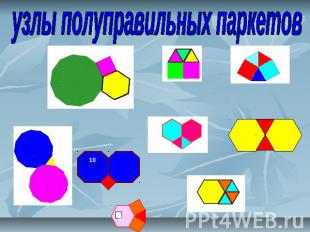
узлы полуправильных паркетов

конец