Презентация на тему: Геометрические паркеты (9 класс)

«Геометрические паркеты» Автор: Сметанина Карина учащаяся 9 «Б» класса МОУ «СОШ № 76», г. Лесной. Руководитель: Королева Наталия Анатольевна, учитель математики I квалификационной категории.

Цель:подробно изучить паркеты.

Задачи: 1. Изучить литературу о паркетах. 2. Найти исторический материал. 3. Научиться решать задачи.

Гипотеза: количество правильных паркетов бесчисленное множество.

Что такое паркет? Паркет - это такое покрытие плоскости многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек.

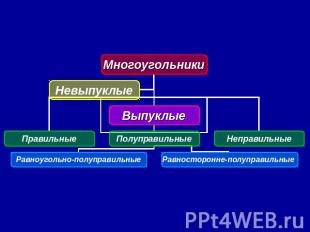
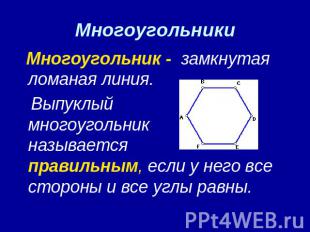
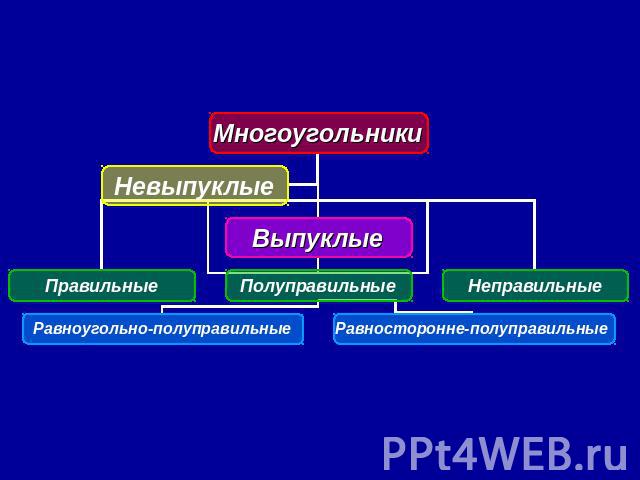
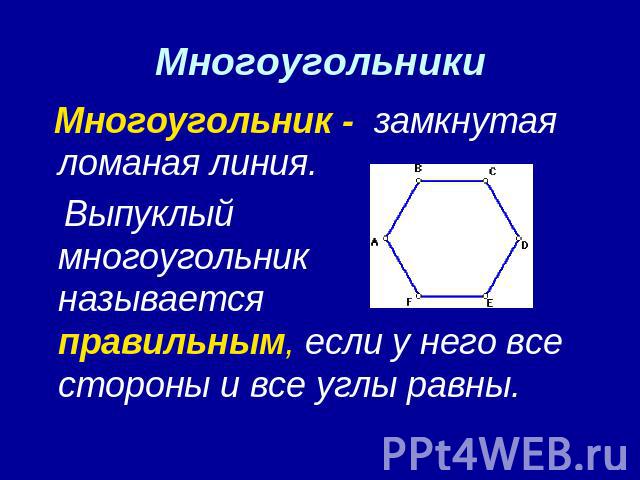
Многоугольники Многоугольник - замкнутая ломаная линия. Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.

Полуправильные многоугольники I) Выпуклый многоугольник с четным числом вершин называется равноугольно-полуправильным, если его стороны, взятые через одну, равны и все его углы равны. II) Выпуклый многоугольник с четным числом вершин называется равносторонне-полуправильным, если его углы, взятые через один, равны и все его стороны равны.

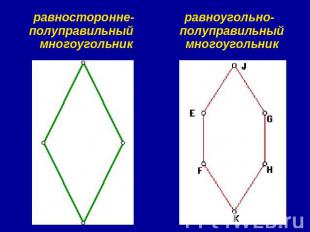
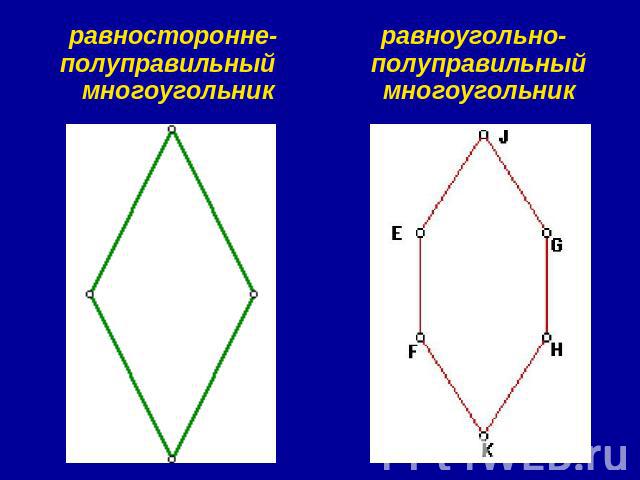
равносторонне-полуправильный многоугольник равноугольно-полуправильный многоугольник

Правильные паркеты Паркет называется правильным, если он составлен из правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом.

Правильные паркеты

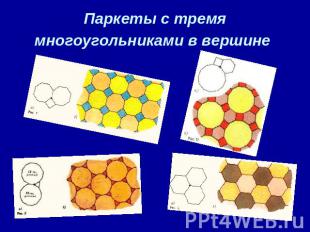
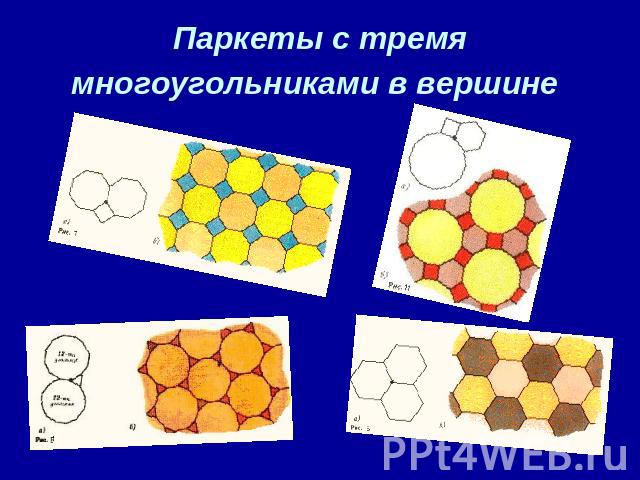
Паркеты с тремя многоугольниками в вершине

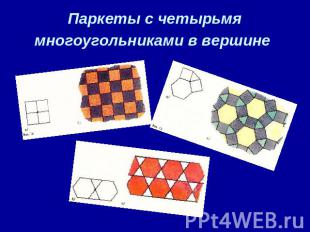
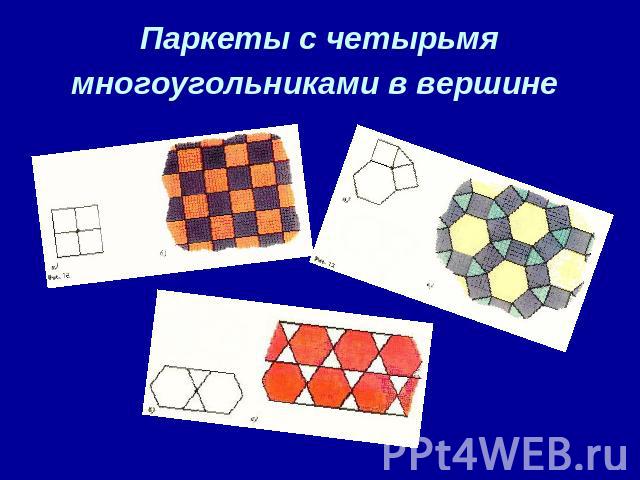
Паркеты с четырьмя многоугольниками в вершине

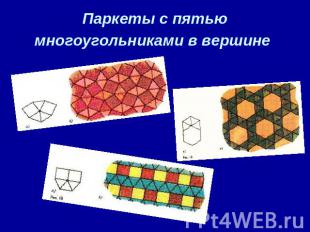
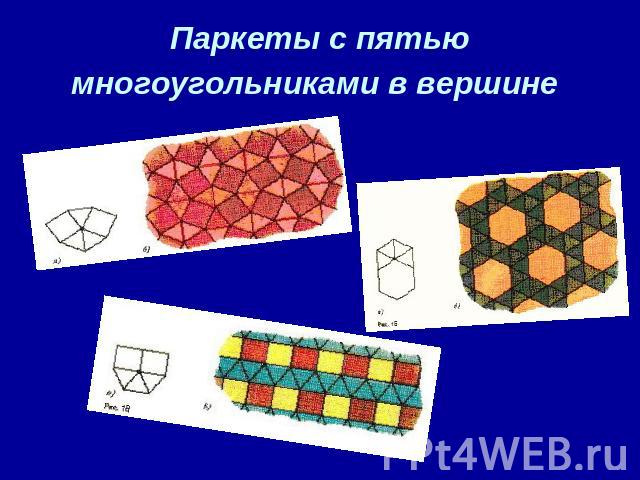
Паркеты с пятью многоугольниками в вершине

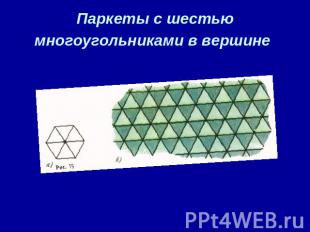
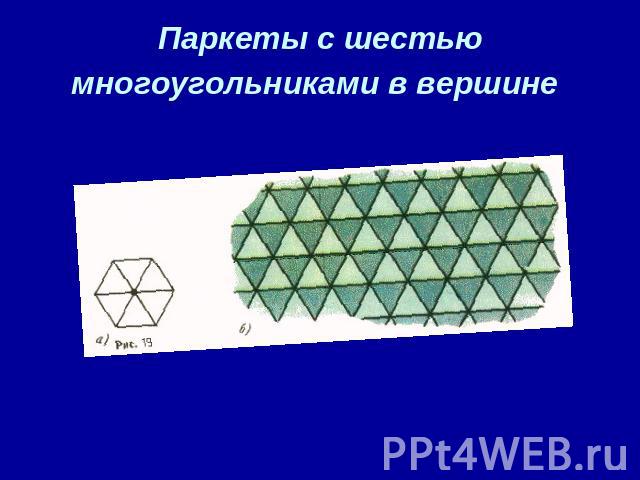
Паркеты с шестью многоугольниками в вершине

Паркеты из неправильных многоугольников Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:

Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма. Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами.

Паркеты из произвольных фигур

Задачи Докажите, что для любого четырехугольника существует паркет, состоящий из четырехугольников равных исходному. Иначе говоря, четырехугольником произвольной формы можно заполнить всю плоскость.

Я считаю, что цель моей работы достигнута. Выдвинутая мною гипотеза о бесконечном множестве правильных паркетов оказалась неверна: в ходе работы я выяснила, что правильных паркетов только 11.

1. Васильев Н.Б. и др. Математические соревнования. Геометрия. - М.: Наука, 1974, с. 15 /Библиотечка физико-математической школы, выпуск 4.2. Доморяд А.П. Математические игры и развлечения. - М.; 1961.3. Журнал //Квант. 1979. - № 2. - С.9; 1980. - № 2. - С.25; 1986 - № 8 - С 3* 1987. - № 6. - С.27; 1987. - № 11. - С.21; 1989. - № 11. - С.57.4. Журнал //Математика в школе. 1967. – № 3. – С.75; 1986. № 1. – С.59;5. Заславский А. Паркеты и разрезания //Квант. - 1999. - № 2. - С.32.6. Кокстер Г.С.М. Введение в геометрию. - М.- Наука, 1966, с. 100.7. Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995.8. Смирнова И.М., Смирнов В.А. Паркеты и их иллюстрации в графическом редакторе "Paint" //Математика в школе. - 2000. - № 8. - С.54.

Спасибо за внимание