Презентация на тему: От натурального числа до мнимой единицы

От натурального числа до мнимой единицы Региональном конкурс ученических творческих работ по математике«Математика в моей жизни – 2009» Выполнил ученик 11 «Б» класса Духанов Данил.Образовательное учреждение:МОУ СОШ №2 г. ПугачёваРуководитель:учитель высшей категорииГорина Т. Е.

«Если бы не число и его природа, ничтосуществующее нельзя было бы постичь имсамо по себе, ни в его отношениях к другимвещам. Мощь чисел проявляется во всехдеяниях и помыслах людей, во всех ремеслах и в музыке» Пифагореец Филолай, 5 в. до н. э. Понятие числа является основным стержнем всего школьного курса математики, пронизывающим этот курс от первого до последнего класса. И, конечно, только в старших классах уместен достаточно полный, систематизирующий взгляд на общую картину завершившегося эволюционного процесса. Я решил написать свою работу учителям математики в поддержку уроков, а также же для расширения кругозора учеников, особо интересующихся математикой.

Цель моей работы: рассказать об истории возникновении большинства существующих видов чисел, отдельно рассмотреть комплексные числа, выяснить насколько они полезны и найти их практическое применение.

Задачи: 1. Собрать материал по своей теме, «провести» слушателей по всей истории возникновения чисел.2. Подробно рассказать о комплексных числах.3. Выяснить, а нужны ли вообще комплексные числа в современном мире? 4. Найти применение комплексных чисел в различных отраслях науки.

Давным - давно… Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел. Самым первым инструментом счета у древнего пещерного человека, безусловно, были пальцы рук. Сама природа предоставила человеку сей универсальный счетный инструмент. У многих народов пальцы (или их суставы) при любых торговых операциях выполняли роль первого счетного устройства. Для большинства бытовых потребностей людей их помощи вполне хватало. К счету по пальцам рук восходят многие системы счисления, например пятеричная (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног), сорокаричная (суммарное число пальцев рук и ног у покупателя и продавца). У многих народов пальцы рук долгое время оставались инструментом счета и на наиболее высоких ступенях развития.

Развитие числа Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа , чтобы

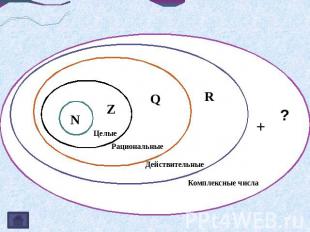
Развитие числа Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений нужно только действовать над такими выражениями по правилам обычной алгебры и считать, что Кардано называл такие величины “чисто отрицательными”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Итак, в настоящем времени существует семь общепринятых уровней обобщения чисел: натуральные, рациональные, действительные, комплексные, векторные, матричные и трансфинитные (последние я упомянул лишь для ознакомления, они изучаются только на последних курсах высшей математики).

Исторические фактыВпервые мнимые величины появились в работе Дж. Кардано «Великое искусство, или об алгебраических правилах» в 1545 году.Пользу мнимых чисел при решении кубических уравнений впервые оценил итальянский ученый Р. Бомбелли (1572).Символ i (imaginaire) предложил российский ученый Л. Эйлер (1794).Задача о выражении степени n из комплексного числа была в основном решена в работах английских ученых А. Муавра (1707, 1724) и Р. Котеса (1722).Термин «комплексное число» ввел французский ученый Л. Карно (1803).В употребление термин вошел после работ К. Гаусса (1831).Полное геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе датского ученого К. Весселя (1799).Геометрическое представление комплексных чисел называют иногда «диаграммой Аргана» в честь швейцарского ученого Ж. Аргана. 

Общий вид комплексного числа: z = a + bi,где a и b – действительные числа, а i = . a называют действительной частью числа и обозначают Re, b – мнимой, обозначают Im.

Сопряжённые числа Если z = a + biz = a – bi,то произведением и суммой сопряжённых чисел являются действительные числа:

Действия с комплексными числами Сумма: (a + bi) + (c + di) = (a + c) + (b + d)i Вычитание: (a + bi) – (c + di) = (a – c) + (b – d)i.Произведение: (a + bi) ∙ (c + di) = (ac – bd) + (ad + bc) i. Деление:

Примеры: Найти разность и частное комплексных чисел

Решение квадратных уравнений с помощью комплексных чисел Квадратные уравнения можно решать с помощью комплексных чисел (Если D < 0, то Например, уравнение:z2 - 3z + 8,5 = 0, D = -25, z1, 2 =

Модуль комплексного числа Модулем комплексного числа называют длину вектора, соответствующего числу. Численно он равен корню из произведения двух сопряженных чисел:r = |z| = |a + bi| =

Тригонометрическая форма записи комплексных чисел В прямоугольном треугольнике OMN длины катетов ON и OM равны соответственно a и b, а длина гипотенузы OM равна |z|. Из тригонометрии известно, что отношение длины катета к длине гипотенузы равняется косинусу прилежащего угла и синусу противолежащего. Следовательно:a = Re z = | z | ∙ cos φ,b = Im z = | z | ∙ sin φ, где φ – аргумент комплексного числа z.Радиус-вектор OM соответствует комплексному числу z = a + bi

Тригонометрическая форма записи комплексных чисел Таким образом:z = a + bi = |z| ∙ cos φ + |z| ∙ sin φ ∙ i = |z| ∙ (cos φ + i sin φ). Произведение двух комплексных чисел будет равно:z1 ∙ z2 = |z1| ∙ |z2| (cos (φ1 + φ2) + i sin (φ1 + φ2)).При умножении комплексных чисел их модули необходимо перемножить, а аргументы – сложить.При делении необходимо произвести обратные операции: поделить модули и вычесть аргументы.

Формы записи комплексных чисел Алгебраическая z =a + biТригонометрическаяz = r (cos φ + i sin φ)Показательнаяz = r e iφ , e iφ = (cos φ + i sin φ) – формула Эйлера

Применение комплексных чисел в планиметрии Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, что |MA|2+|MC|2=|MB|2+|MD|2, то ABCD - прямоугольник. Решение. Если за начальную точку принять центр параллелограмма ABCD, то при принятых ранее обозначениях с = -a, d= -b, и поэтому данное в условии равенство будет эквивалентно равенству , которое означает, что диагонали параллелограммаравны, т. е. он прямоугольник.

Формула Муавра Формулой Муавра называют выражение, получаемое при возведение комплексного числа в степень n:zn = rn (cos nφ + i sin nφ). Для любого Z= r (cos φ+ i sin φ)≠0 и любого натурального числа n Абрамах Муавр (Moivre) (1667 – 1754)

Карл Фридрих Гаусс (Gauss)(1777 – 1855) Карл Фридрих Гаусс – немецкий математик. Работы Гаусса оказали большое влияние на развитие теории чисел.

Леонард Эйлер (Eular)(1707 – 1783) Леонард Эйлер - математик, академик Петербургской академии наук. В его трудах многие математические формулы и символика впервые получают современный вид (ему принадлежат обозначения для e, , i).

Василий Сергеевич Владимиров(1923 – ) Василий Сергеевич - советский и российский математик, академик, Герой Социалистического Труда (1983), лауреат Сталинской премии (1953) и Государственной премии СССР (1987), доктор физико-математических наук.Основные труды по вычислительной математике, квантовой теории поля, теории аналитических функций многих комплексных переменных, уравнениям математической физики.

Применение комплексных чисел Сегодня сложно представить себе ряд наук без применения комплексных чисел. Теория электротехники, электромеханики, радиотехники, самолетостроения и других наук невозможна без применения моделей в виде комплексных чисел. Экономика, более сложная наука, до сих пор не знала применения комплексных чисел.

Комплексные числа в экономике Товар является носителем двух составляющих: потребительских свойств, объективно присущих товару, и цены - денежной оценки потребительских свойств товара конкретным потребителем. С учетом того, что и потребительские свойства товара и его цена являются необходимыми показателями свойств товара, возникает потребность разработки и использования комплексного показателя, характеризующего эти две стороны одного объекта. Именно таким показателем может стать комплексное число, состоящее из действительной и мнимой частей.

Комплексные числа в экономике Представив какую-либо оценку потребительских свойств товара П как действительную часть комплексного числа, а его цену Ц - как мнимую часть, получим: Т = П + iЦ

Применение комплексных чисел Большой вклад в развитие теории функций комплексной переменной внесли советские ученые: Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля. Развитие учения о комплексных числах находит себе важнейшие применения в теории электротехники, электромеханики, радиотехники, самолётостроении и других наук. Действия над комплексными числами связаны с важными действиями геометрического характера и имеют значительные и обширные приложения. Также с их помощью можно иногда с большей простотой получить такие результаты, относящиеся к действительным числам, которые без комплексных чисел получаются с большим трудом.Введение комплексных чисел, помимо своего чисто математического значения, представляет собой едва ли не самую яркую на протяжении школьного курса иллюстрацию диалектического развития математических понятий. Совокупность комбинаций вещественного и чисто мнимого чисел образует единое стройное целое – мир комплексных чисел, находящий себе наглядную иллюстрацию в цельном и законченном образе комплексной плоскости. Вряд ли можно подыскать другой пример, который с такой яркостью, наглядностью, логической простотой и вместе с такой исчерпывающей полнотой мог бы иллюстрировать диалектические законы развития математических понятий. Применение комплексных чисел в различных отраслях науки означает, что комплексные числа всё-таки придуманы не зря и нужны для дальнейшего изучения.

Результаты проведения элективного курса в 11 классе

«Мнимые числа – это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием». Г.Лейбниц Итак, в своей работе я представил вам историю возникновения чисел.Подводя итоги, можно сделать вывод: метод комплексных чисел в применении к решению задач по элементарной геометрии можно изучать старшим школьникам на факультативных занятиях, так как этот метод использует аппарат комплексных чисел, что, безусловно, должно заинтересовать увлекающихся математикой учеников. Спасибо за внимание!

Использованная литература А.Г Мордкович, П.В. Семёнов: «Алгебра и начала анализа» 10 класс. Москва: Мнемозина 2007;А.П.Савин: «Энциклопедический словарь юного математика»;Интернет-ресурсы.