Презентация на тему: Парабола

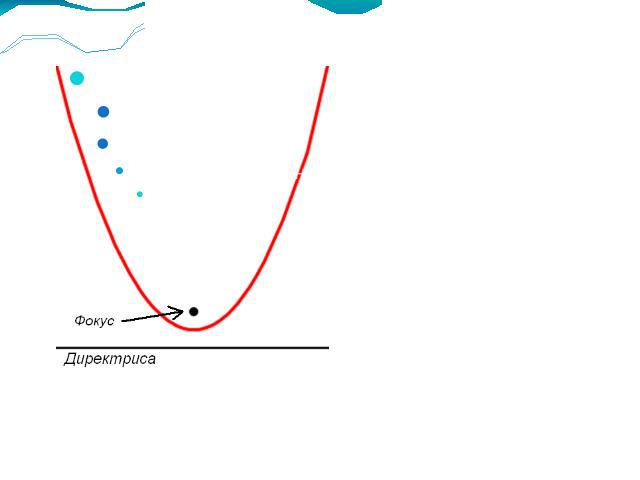
Парабола Понятие Параболой называется множество таких точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку.

ПонятиеПараболой называется множество таких точек плоскости, для которых расстояние до фиксированной точки равно расстоянию до фиксированной прямой, не проходящей через эту точку.

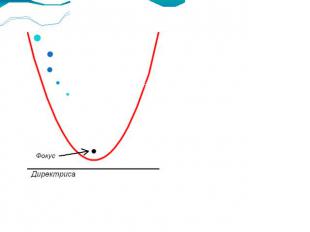
Парабола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

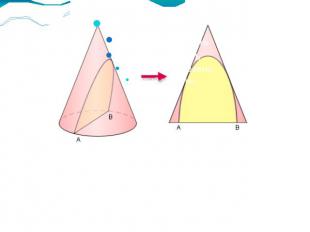
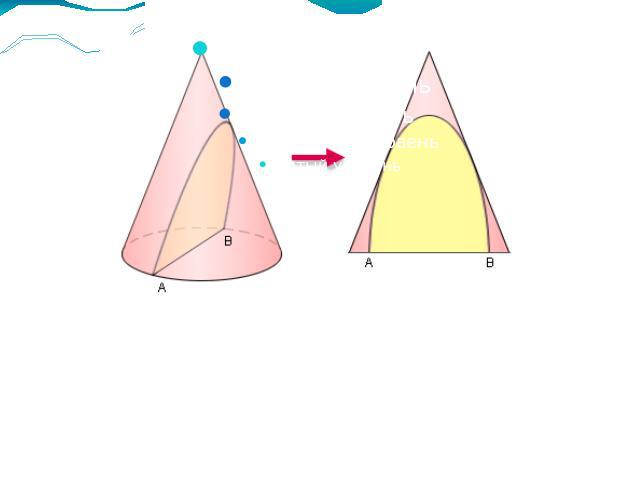
Наряду с эллипсом и гиперболой, парабола является сечением конуса. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Уравнения Каноническое уравнение параболы в прямоугольной системе координат: y2=2px или x2=2py (если поменять оси местами)

Квадратное уравнение y = ax2 + bx + c при a=0 также представляет собой параболу и графически изображается той же параболой, что и y = ax2, но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

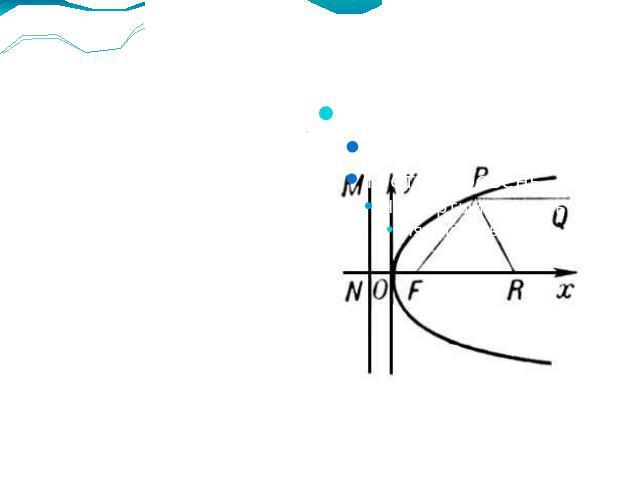
Построение Параболу можно построить «по точкам» с помощью циркуля и линейки, не зная уравнения и имея в наличии только фокус и директрису. Вершина является серединой отрезка между фокусом и директрисой. На директрисе задаётся произвольная система отсчёта с нужным единичным отрезком. Каждая последующая точка является пересечением серединного перпендикуляра отрезка между фокусом и точкой директрисы, находящейся на кратном единичному отрезку расстоянии от начала отсчёта, и прямой, проходящей через эту точку и параллельной оси параболы.

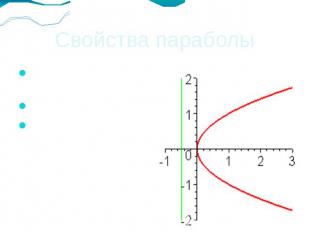
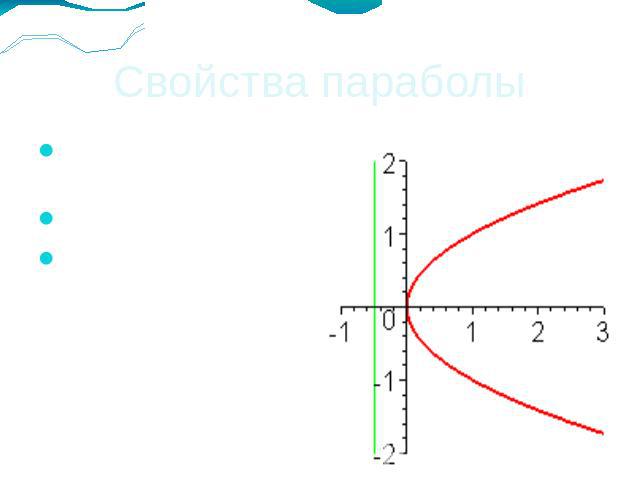
Свойства параболыПарабола имеет 1 ось симметрии.Функция монотонна Неограниченно возрастает

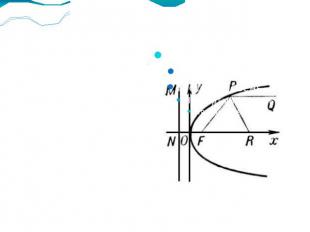
Парабола целиком лежит в полуплоскости (x> 0), граница которой перпендикулярна к оси параболы.

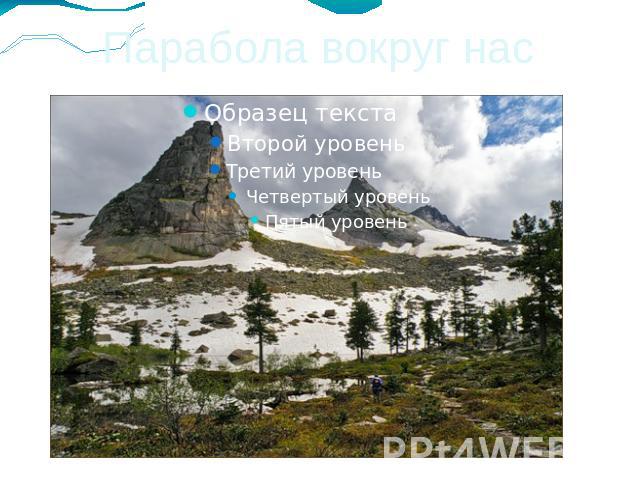
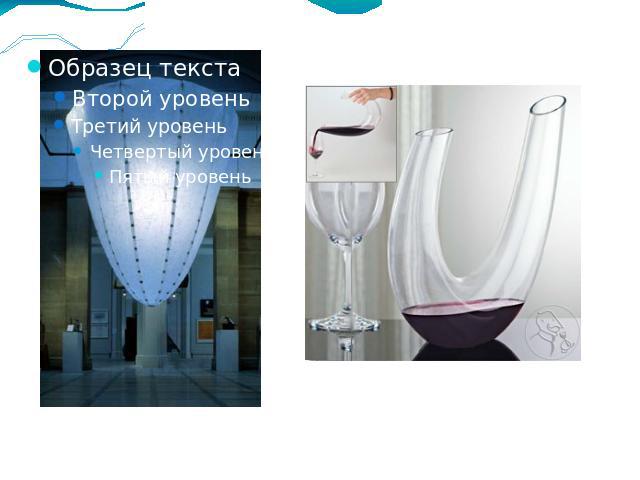
Парабола вокруг нас

Презентацию выполнила ученица 11 а класса Довлекаева Эльвира.