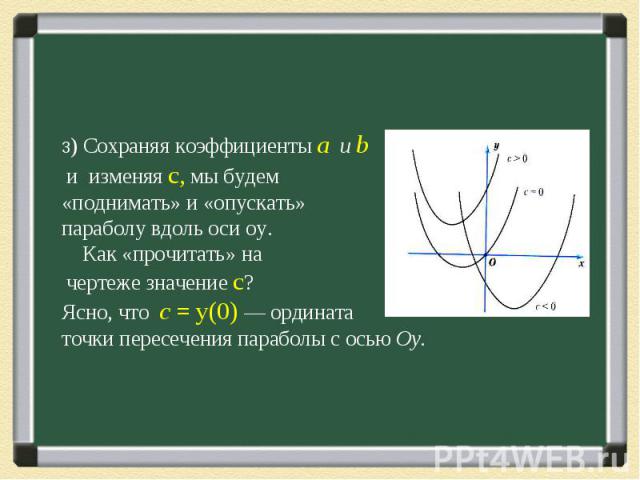
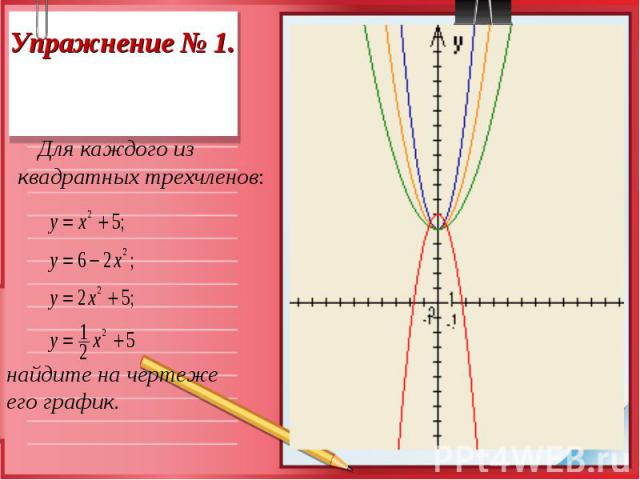
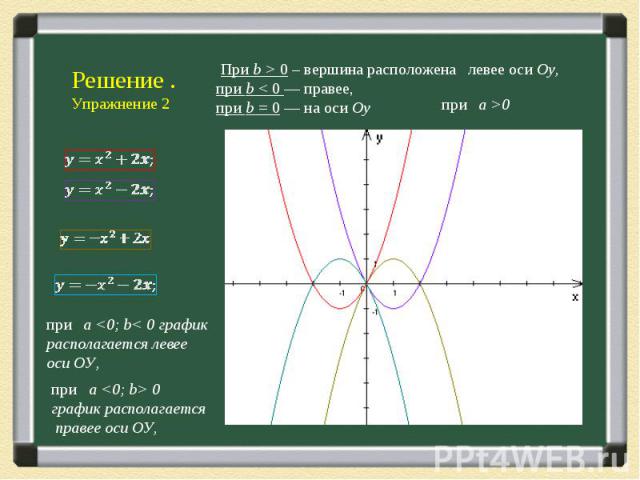
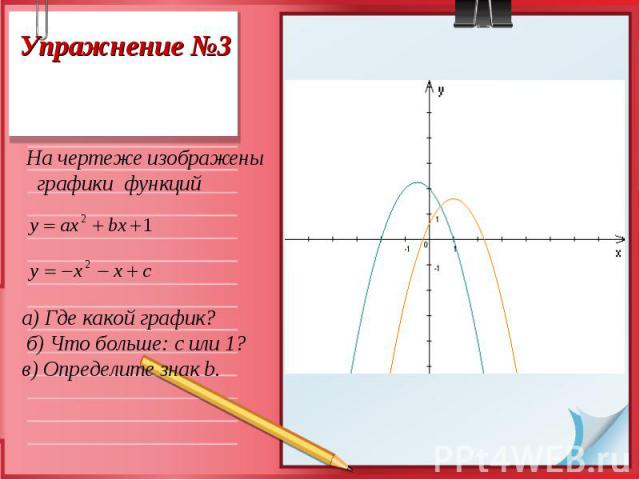
Презентация на тему: Эта замечательная парабола..

Аполлоний Пергский (Ἀπολλώνιος ὁ Περγαῖος, Перге, 262 до н. э. — 190 до н. э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э. Аполлоний Пергский (Ἀπολλώνιος ὁ Περγαῖος, Перге, 262 до н. э. — 190 до н. э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э. Аполлоний прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата «Парабола» означает приложение или притча. Долгое время так называли линию среза конуса, пока не появилась квадратичная функция.

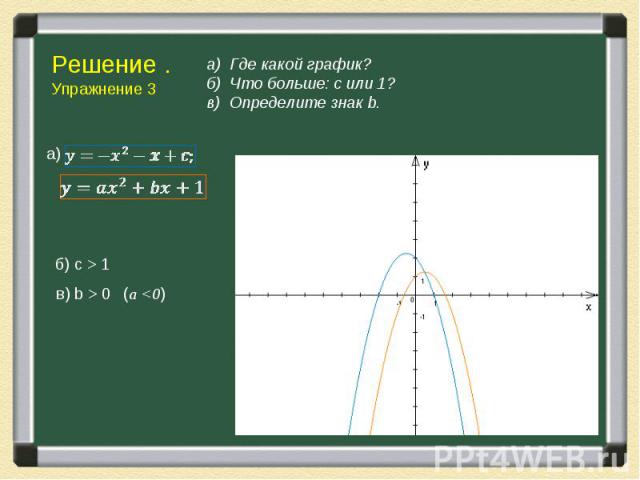
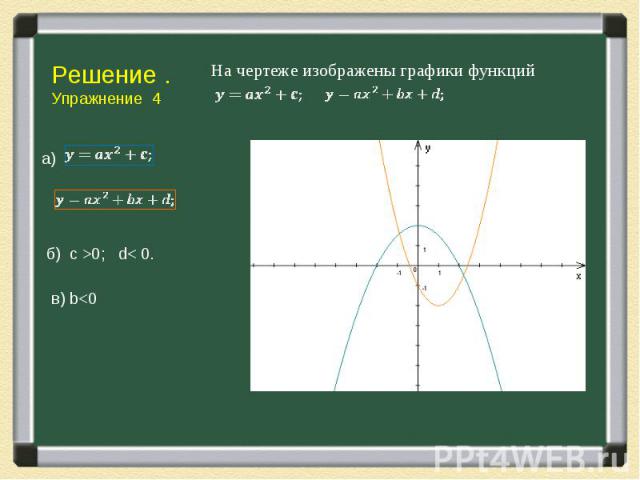
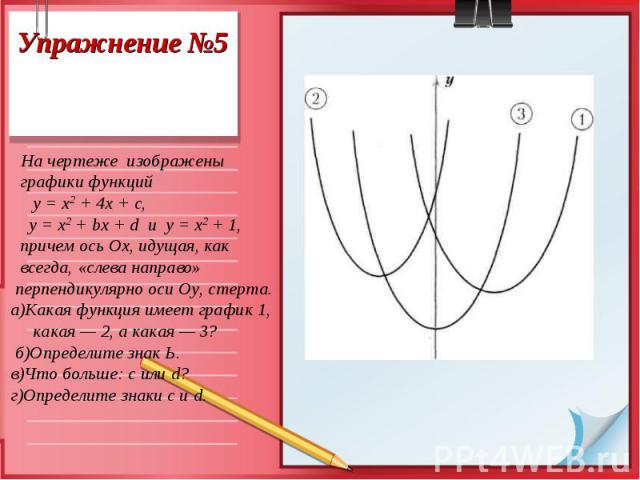
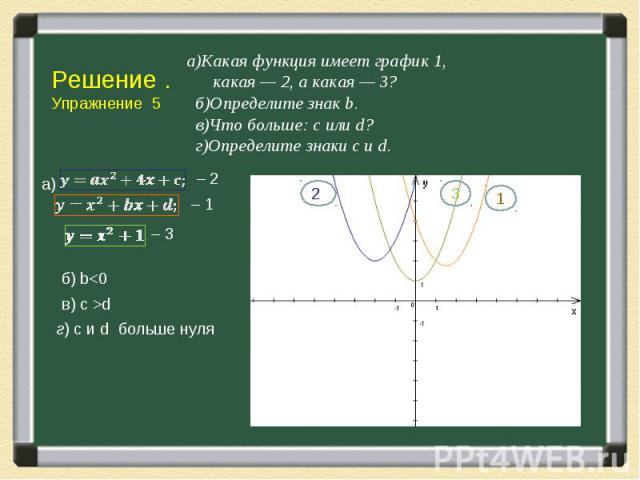
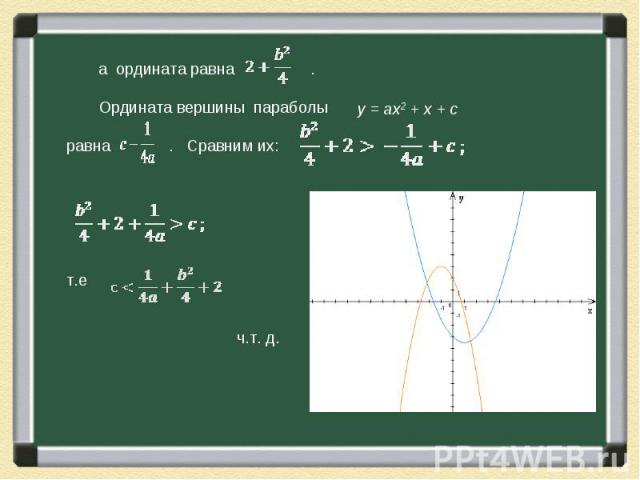
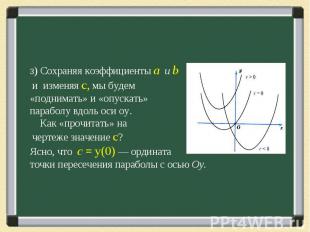
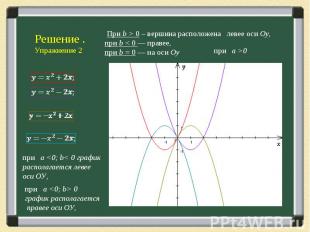
Подумаем, как можно получить массу информации о коэффициентах квадратного трехчлена у =ах2 + bх + с, рассматривая его график — параболу. Сначала напомним хорошо известные факты. 1) Знак коэффициента а (при х2) показывает направление ветвей параболы: а > 0 — ветви вверх; а < 0 — ветви вниз. Модуль коэффициента а отвечает за «крутизну» параболы: чем больше |a|, тем «круче» парабола.

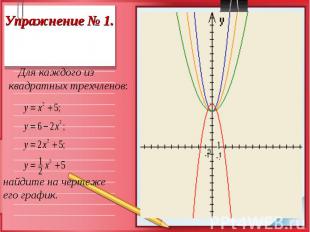
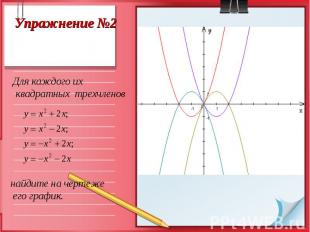
А теперь, когда мы вспомнили как влияют коэффициенты на построение графика параболы выполним следующие упражнения: А теперь, когда мы вспомнили как влияют коэффициенты на построение графика параболы выполним следующие упражнения:

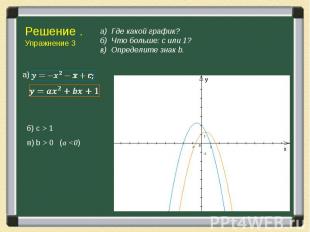
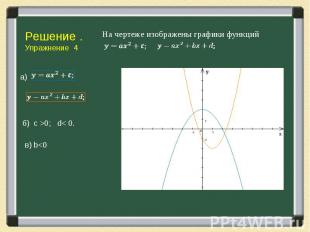
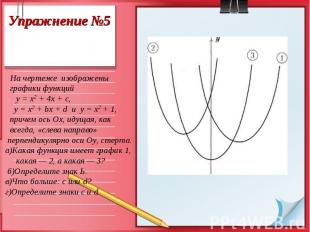
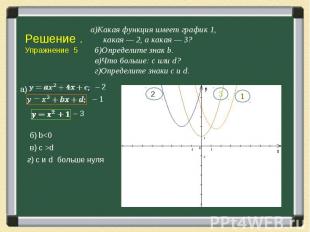
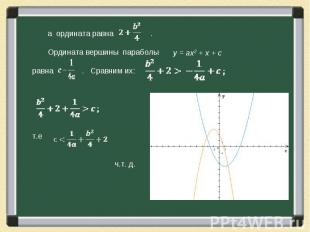
Решение упражнений основывается на тех фактах, которые мы знаем о коэффициентах квадратного трехчлена. Решение упражнений основывается на тех фактах, которые мы знаем о коэффициентах квадратного трехчлена. Свойства параболы чрезвычайно богаты и разнообразны, используя их решите следующую задачу.  

Известно, что парабола, являющаяся графиком квадратного трехчлена у = ах2 + 10х + с, не имеет точек в третьей четверти. Какое из следующих утверждений может быть неверным? Известно, что парабола, являющаяся графиком квадратного трехчлена у = ах2 + 10х + с, не имеет точек в третьей четверти. Какое из следующих утверждений может быть неверным? (A) а>0 (B) Вершина параболы лежит во второй четверти. (C) с ≥ 0 (D) c > 0,1 (Е) 1ОО – 4 ас ≤ 0.

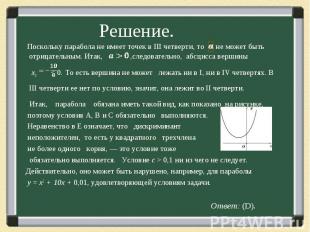
Поскольку парабола не имеет точек в III четверти, то не может быть отрицательным. Итак, ,следовательно, абсцисса вершины Поскольку парабола не имеет точек в III четверти, то не может быть отрицательным. Итак, ,следовательно, абсцисса вершины х0 < 0. То есть вершина не может лежать ни в I, ни в IV четвертях. В III четверти ее нет по условию, значит, она лежит во II четверти. Итак, парабола обязана иметь такой вид, как показано на рисунке, поэтому условия А, В и С обязательно выполняются. Неравенство в Е означает, что дискриминант неположителен, то есть у квадратного трехчлена не более одного корня, — это условие тоже обязательно выполняется. Условие с > 0,1 ни из чего не следует. Действительно, оно может быть нарушено, например, для параболы у = х2 + 10х + 0,01, удовлетворяющей условиям задачи. Ответ: (D).

Самые близкие родственники параболы – это Самые близкие родственники параболы – это окружность, гипербола и эллипс.