Презентация на тему: Правильные многогранники

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ. Многогранники вокруг нас или мы внутри многогранника?Бурцева Елена Васильевна МОУ СОШ №19 пос. Пироговский Мытищинского района

Цель: Познакомить учащихся с многогранным миром геометрии.

ЗАДАЧИ: Познакомить учащихся с историей изучения многогранниковДать представление о геометрическом строении многогранников, их свойствахРазвить у учащихся способность видеть связь между математической теорией и реальным миром, различными сферами жизни и деятельности человека, общества.

Определение: многогранник называется правильным, если все его грани правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число рёбер.Существует 5 видов правильных многогранников. ТЕТРАЭДРГЕКСАЭДРОКТАЭДРИКОСАЭДРДОДЕКАЭДР

Названия многогранников пришли из Древней Греции и в них указывается число граней: «эдра» - грань«тетра» - 4«гекса» - 6«окта» - 8«икоса» - 20«дедека» - 12

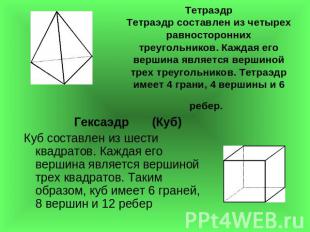
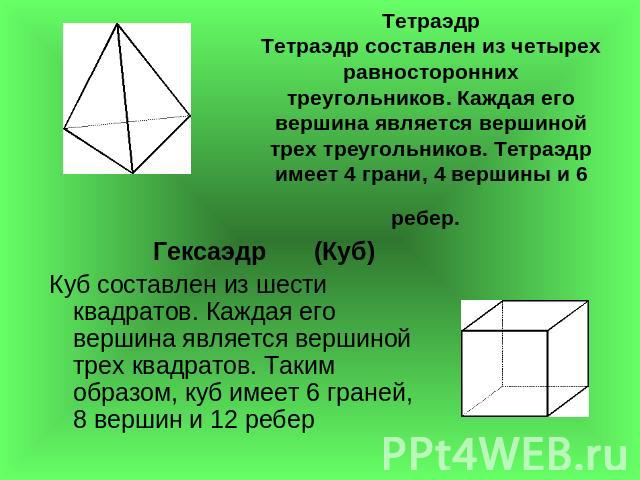
ТетраэдрТетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Тетраэдр имеет 4 грани, 4 вершины и 6ребер. Гексаэдр (Куб)Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер

ОктаэдрОктаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. ИкосаэдрИкосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Икосаэдр имеет 20 граней, 12 вершин и 30 ребер

ДодекаэдрДодекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2. Г+В=Р+2

«Правильные многогранники в философской картине мира Платона» Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

«Кубок Кеплера» Иоганн Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.

"Тайнaя вечеря" С. Дали Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра. Учёным достаточно хорошо изучены правильные выпуклые многогранники, доказано, что существует всего пять видов таких многогранников, но сам ли человек их придумал? Скорее всего – нет, он «подсмотрел» их у природы.

«Правильные многогранники и природа»Скелет одноклеточного организма феодарии по форме напоминает икосаэдр . Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли ( NaCl ) имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами , монокристалл которых имеет форму правильного октаэдра

Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана ( FeS ). Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

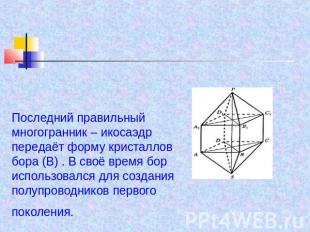
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В) . В своё время бор использовался для создания полупроводников первого поколения.

Вывод: благодаря правильным многогранникам открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

Используемые материалы: www. samara.edu.ru.www. rspu.ruwww.edu.hmao.ruwww. tspu.ruwww.nvp.region.ru