Презентация на тему: Правильные многогранники

Правильные многогранники

СИММЕТРИЯ В ПРОСТРАНСТВЕ “Симметрия является той идеей, посредством которой человек пытался постичь и создать порядок, красоту и совершенство” (Г.Вейль) «Витрувианский человек» Ленардо Да Винчи (1490,Венеция) Симметрия («соразмерность») — соответствие, неизменность (инвариантность), проявляемая при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы, сохраняя одну точку на месте.

СИММЕТРИЯ В ПРОСТРАНСТВЕ Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.

СИММЕТРИЯ В ПРОСТРАНСТВЕ Точки А и А1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе.

СИММЕТРИЯ В ПРОСТРАНСТВЕ Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе

СИММЕТРИЯ В ПРОСТРАНСТВЕ Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией
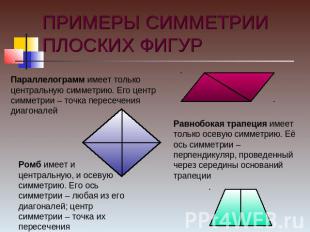
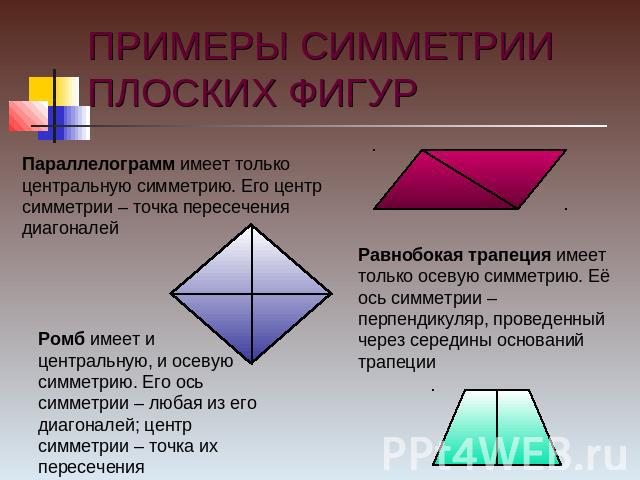
ПРИМЕРЫ СИММЕТРИИ ПЛОСКИХ ФИГУР Параллелограмм имеет только центральную симметрию. Его центр симметрии – точка пересечения диагоналей Ромб имеет и центральную, и осевую симметрию. Его ось симметрии – любая из его диагоналей; центр симметрии – точка их пересечения Равнобокая трапеция имеет только осевую симметрию. Её ось симметрии – перпендикуляр, проведенный через середины оснований трапеции

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ - 5 ПЛАТОНОВЫХ ТЕЛ Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.Также все ребра правильного многоугольника равны, как и все двугранные углы, содержащие две грани с общим ребром.Правильного многогранника, гранями которого являются n-угольники при n > или = 6, не существует! Обитатели даже самой отдаленной галактики не могут играть в кости, имеющие форму неизвестного нам правильного выпуклого многогранника. М. Гарднер

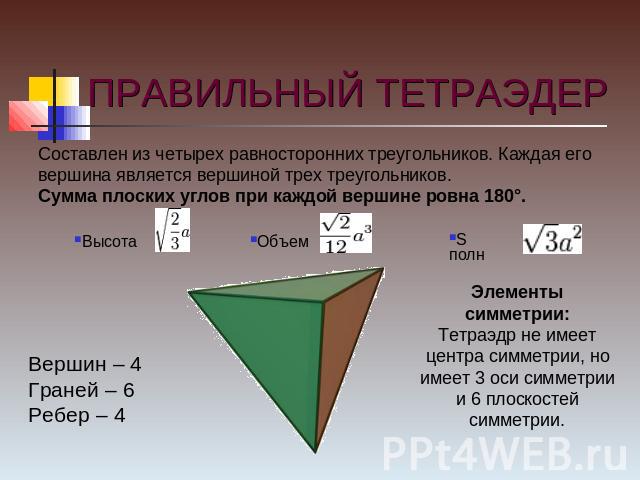
ПРАВИЛЬНЫЙ ТЕТРАЭДЕР Составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников.Сумма плоских углов при каждой вершине ровна 180°. Вершин – 4Граней – 6Ребер – 4 Элементы симметрии:Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
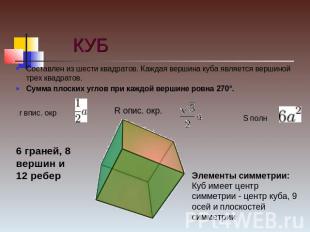
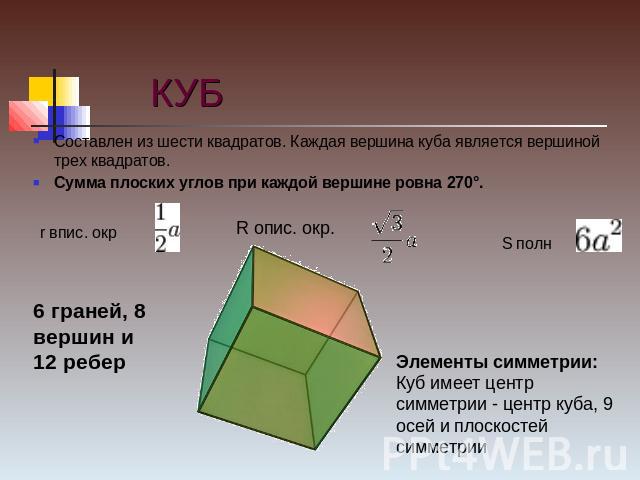
КУБ Составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов.Сумма плоских углов при каждой вершине ровна 270°. 6 граней, 8 вершин и 12 ребер Элементы симметрии: Куб имеет центр симметрии - центр куба, 9 осей и плоскостей симметрии

ПРАВИЛЬНЫЙ ОКТАЭДР Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников.Сумма плоских углов при каждой вершине равна 240°. 8 граней 6 вершин 12 ребер Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии

ПРАВИЛЬНЫЙ ИКОСАЭДР Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольниковСумма плоских углов при каждой вершине равна 300°20 граней, 12 вершин и 30 ребер Элементы симметрии: Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии

ПРАВИЛЬНЫЙ ДОДЕКАЭДР Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.Сумма плоских углов при каждой вершине ровна 324°12 граней, 20 вершин и 30 ребер Элементы симметрии: Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

СПАСИБО ЗА ВНИМАНИЕ!