Презентация на тему: Построение графиков функций, содержащих переменную под знаком модуля

Построение графиков функций, содержащих переменную под знаком модуля

1. Построение графиков функций вида y=|f(x)|. По определению модуля, выражение y=|f(x)| равносильно системе f(x), если f(х)0, Y= -f(x), если f(x)<0. Значит, для того чтобы построить график функции y=|f(x)|, нужно построить сначала график функции y=f(x), ту часть графика, которая расположена выше оси Х, оставить без изменений, а расположенную ниже - отобразить симметрично относительно оси Х.

Пример 1. Построить график функции у=|х-3|. Решение. Сначала построим график функции у=х-3:При х=о у=-3,при х=3 у=0(рис.1а).Часть графика, расположенную ниже оси абсцисс, отобразим симметрично относительно оси Х, а другую - оставим без изменений. Полученный график -искомый(рис.1б).

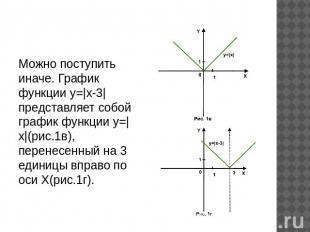
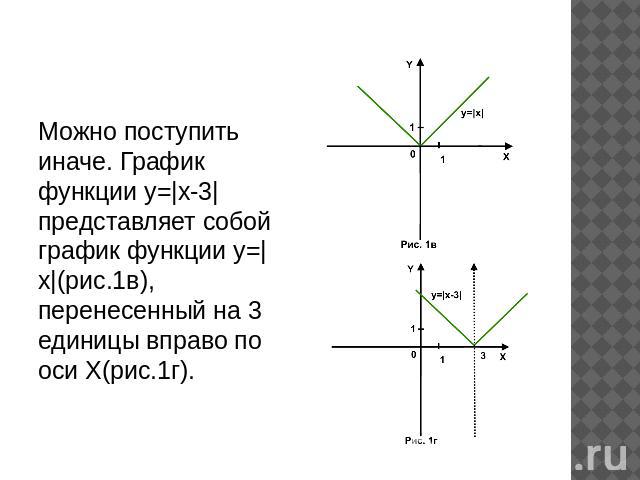
Можно поступить иначе. График функции у=|х-3| представляет собой график функции у=|x|(рис.1в), перенесенный на 3 единицы вправо по оси Х(рис.1г).

Вообще, графики функций вида у=|x+a|+b можно получить из графика функции у=|х| переносом его на а единиц по оси Х вправо, если a<0, или влево, если а>0, и на b единиц по оси У вверх, если b>0, или вниз, если b<0

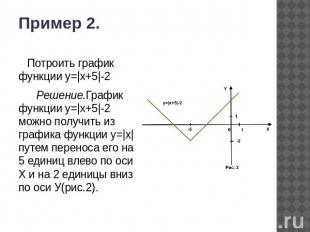
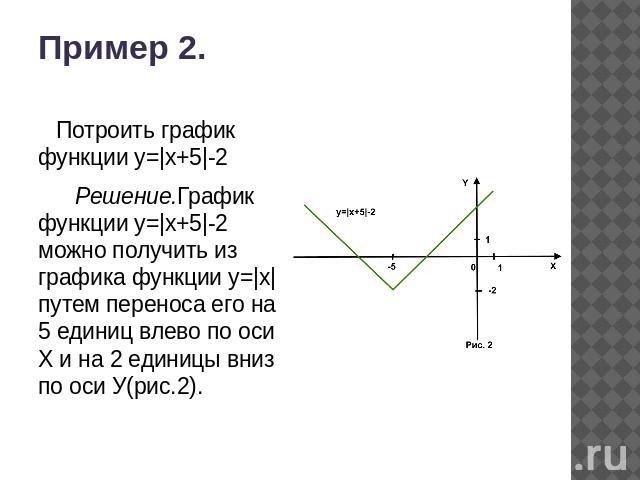
Пример 2. Потроить график функции у=|х+5|-2 Решение.График функции у=|х+5|-2 можно получить из графика функции у=|х| путем переноса его на 5 единиц влево по оси Х и на 2 единицы вниз по оси У(рис.2).

2. Построение графика функции вида y=f(|x|). По определению модуля, выражение y=f(|x|) равносильно системе f(x), если х≥0,у= f(-x), если х<0. Значит, чтобы построить график функции y=f(|x|), нужно сначала построить график функции y=f(|x|), часть графика, расположенную в правой полуплоскости (правее оси абсцисс) оставить без изменений и отобразить её симметрично оси У, отбросив часть графика, расположенную в левой полуплоскости.

Пример 3. Построить график функции у=х2-2|х|-3. Решение. По свойству модуля, х2=|х|2, значит у=х2-2|х|-3 можно представить в виде у=|х|2-2|х|-3. Тогда для того чтобы построить график у=х2-2|х|-3 нужно построить график функции у=х2-2х-3:х0=-b/2a=-(-2)/2=1, y0=y(1)=1-2-3=-4,ось параболы х=1, её вершина имеет координаты (1;-4),при у=0 х=3 или х=-1,при х=0 у=-3(рис.3а). Теперь оставим без изменений часть графика, расположенную в правой полуплоскости, и отобразим её симметрично относительно оси У(другую часть графика отбросим)(рис.3б).

3. Построение графика функции вида Y=|f(X)|+|G(x)|. Для построения графика функций такого вида нужно найти нули каждой функции под знаком модуля и нанести их на координатную прямую. На каждом из полученных промежутков необходимо раскрыть модули по определению, т.е. в зависимости от знака функции под модулем на данном промежутке. Затем нужно построить каждую из полученных функций у на их области определения; полученный график - искомый.

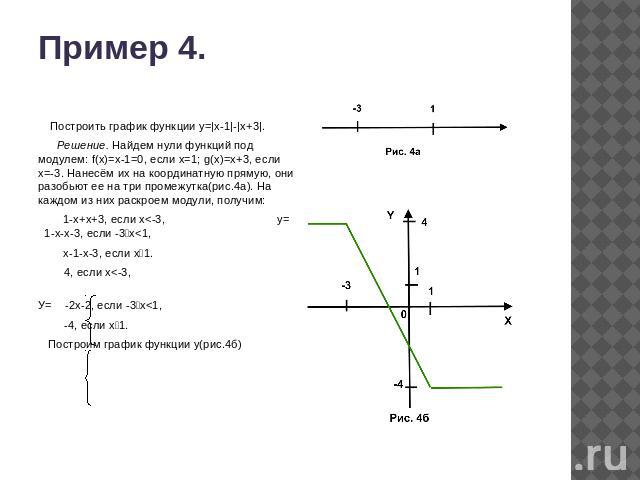
Пример 4. Построить график функции y=|x-1|-|х+3|. Решение. Найдем нули функций под модулем: f(x)=x-1=0, если х=1; g(x)=х+3, если х=-3. Нанесём их на координатную прямую, они разобьют ее на три промежутка(рис.4а). На каждом из них раскроем модули, получим: 1-х+х+3, если х<-3, у= 1-х-х-3, если -3х<1, х-1-x-3, если х1. 4, если х<-3, У= -2х-2, если -3х<1, -4, если х1. Построим график функции у(рис.4б)

4.Построение графика функции вида Y=|||f(x)|+a|+b|. Для построения графика такой функции необходимо сначала построить график функции внутреннего модуля(у=|f(x)|), потом преобразовать его в график у=||f(x)|+a|, затем - в график у=|||f(x)|+a|+b|, т.е. последовательно раскрывать модули, начиная с внутреннего.

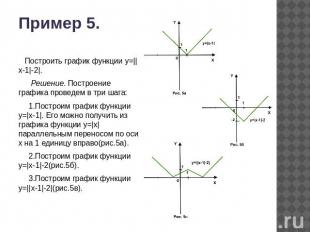
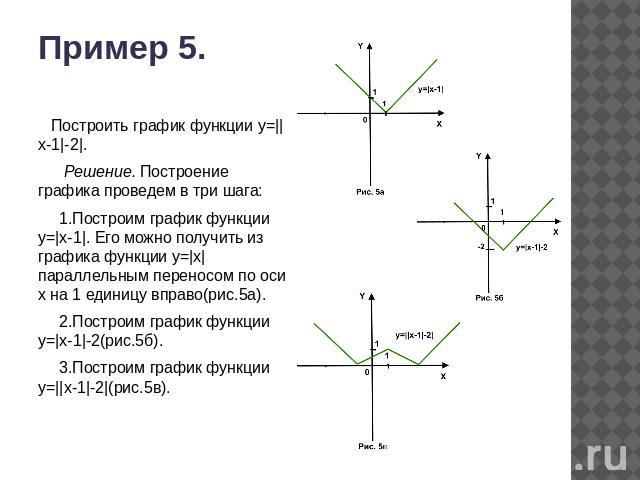
Пример 5. Построить график функции у=||x-1|-2|. Решение. Построение графика проведем в три шага: 1.Построим график функции у=|x-1|. Его можно получить из графика функции у=|x| параллельным переносом по оси х на 1 единицу вправо(рис.5а). 2.Построим график функции у=|x-1|-2(рис.5б). 3.Построим график функции у=||x-1|-2|(рис.5в).

5. Построение графика функции вида y=g(X)|f(x)|. 5.1.Если g(X)=a, то у=а|f(x)|. Тогда график функции у=а|f(x)| можно получить из графика функции у=|f(x)|его сжатием в а раз к оси у, если а>1;его растяжением в 1/а раз к оси у, если 1<a<0;симметрией относительно оси х, если а<0.

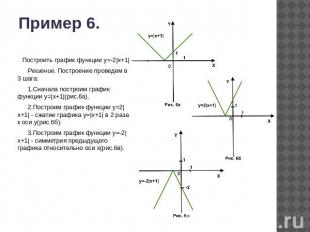
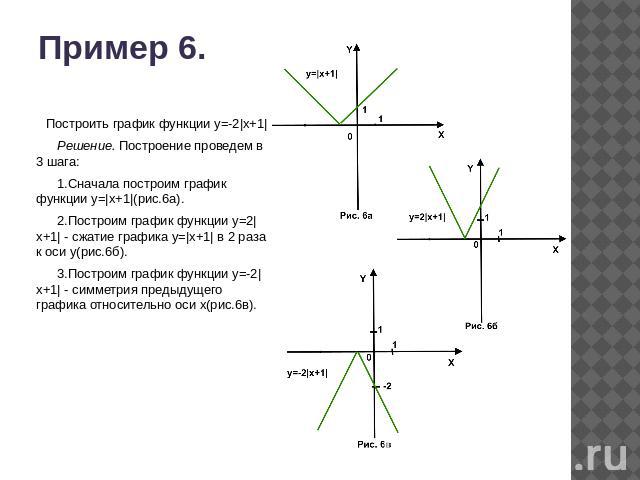
Пример 6.Построить график функции у=-2|x+1| Решение. Построение проведем в 3 шага: 1.Сначала построим график функции у=|x+1|(рис.6а). 2.Построим график функции у=2|x+1| - сжатие графика у=|x+1| в 2 раза к оси у(рис.6б). 3.Построим график функции у=-2|x+1| - симметрия предыдущего графика относительно оси х(рис.6в).

5.2.Если g(x)a, то находим нули функции под модулем и наносим их на координатную прямую. Раскрываем модуль на получившихся промежутках по определению и перемножаем функции.

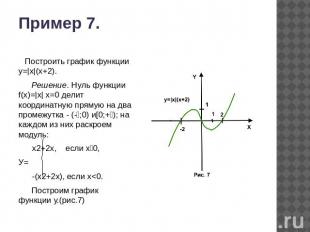
Пример 7. Построить график функции у=|х|(х+2). Решение. Нуль функции f(x)=|х| х=0 делит координатную прямую на два промежутка - (-;0) и[0;+); на каждом из них раскроем модуль: х2+2x, если х0,У= -(х2+2х), если х<0. Построим график функции у.(рис.7)

6. Построение графика функции вида |y|=f(x). По определению модуля, выражение |у|=f(x) равносильно системе y, если y0,f(x)= -y, если у<0. Значит, чтобы построить график функции |у|=f(x), необходимо сначала построить график функции у=f(x), его часть, расположенную выше оси Х, оставить без изменений и , отбросив часть, расположенную ниже оси Х, отобразить симметрично относительно оси Х.

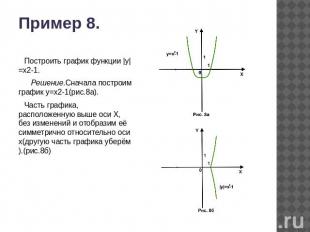
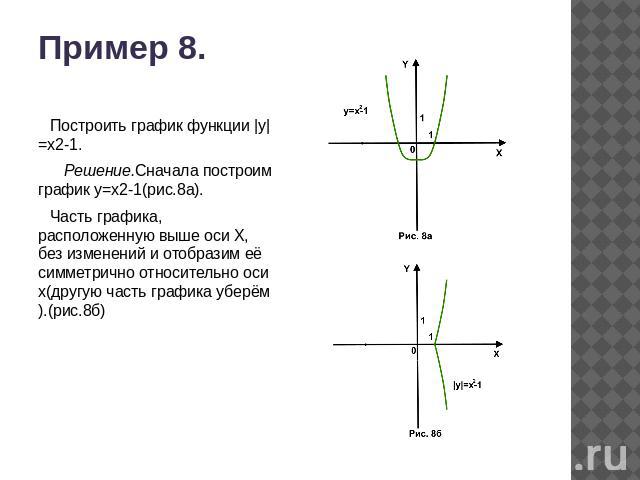
Пример 8.Построить график функции |у|=х2-1. Решение.Сначала построим график у=х2-1(рис.8а).Часть графика, расположенную выше оси Х, без изменений и отобразим её симметрично относительно оси х(другую часть графика уберём).(рис.8б)

7. Построение графиков функций вида |y|=f(|x|) и |y|=|f(x)|. Для построения графиков функций такого вида нужно построить график функции y=f(x) и применить операцию модуль сначала для правой части(построить графики функций у=f(|x|) или у=|f(x)| соответственно), а потом для левой (применить операцию модуль, как описано в 6 пункте.

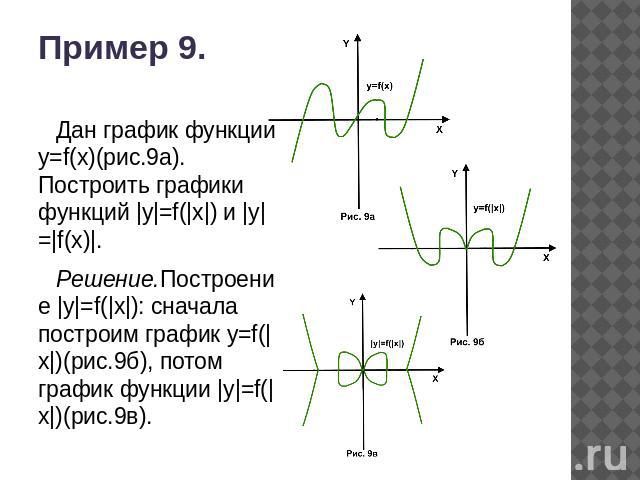
Пример 9. Дан график функции y=f(x)(рис.9а). Построить графики функций |y|=f(|x|) и |y|=|f(x)|.Решение.Построение |y|=f(|x|): сначала построим график y=f(|x|)(рис.9б), потом график функции |y|=f(|x|)(рис.9в).

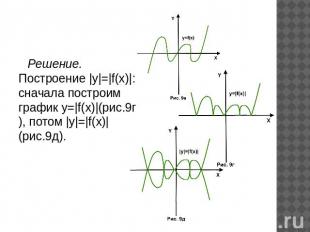
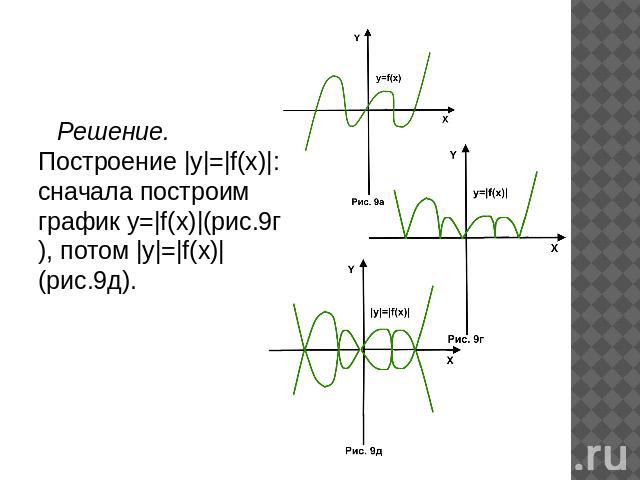
Решение. Построение |y|=|f(x)|: сначала построим график y=|f(x)|(рис.9г), потом |y|=|f(x)|(рис.9д).