Презентация на тему: Преобразование графиков функций, содержащих модуль

Преобразование графиков функций, содержащих модуль
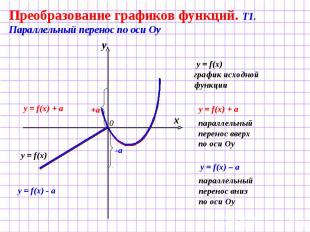
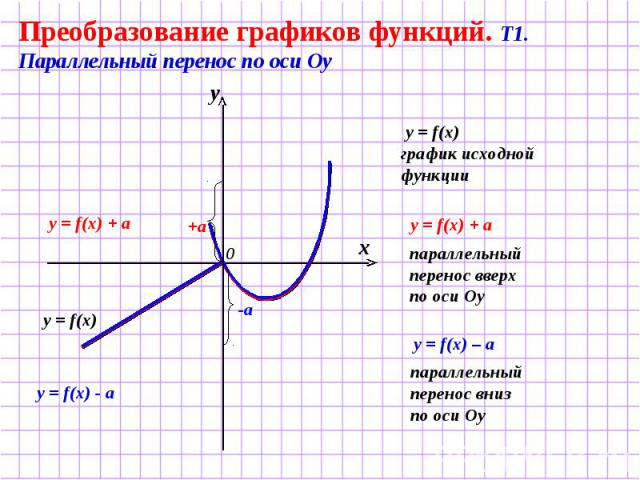
Преобразование графиков функций. Т1. Параллельный перенос по оси Оу y = f(x) график исходной функции параллельный перенос вверх по оси Оу параллельный перенос вниз по оси Оу
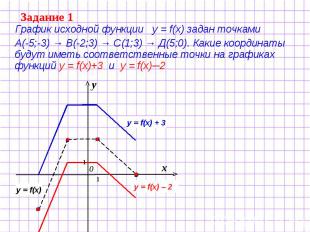
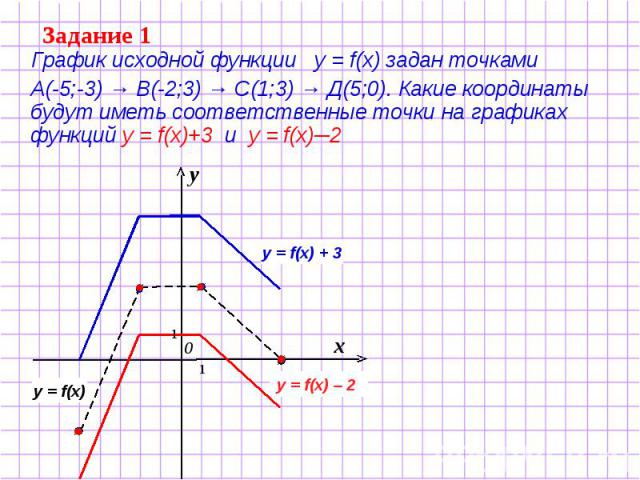
Задание 1 График исходной функции у = f(x) задан точками А(-5;-3) → В(-2;3) → С(1;3) → Д(5;0). Какие координаты будут иметь соответственные точки на графиках функций у = f(x)+3 и у = f(x)─2

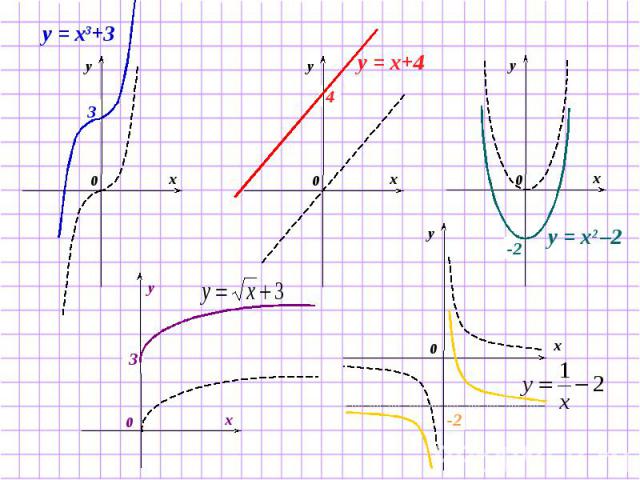
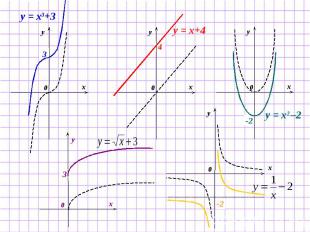
Задание 2 Назовите функции, графики которых можно построить путем параллельного переноса исходного графика вдоль оси Оу : у = (х–8)2 у = х3+3 у = х + 4 у = х2 – 2
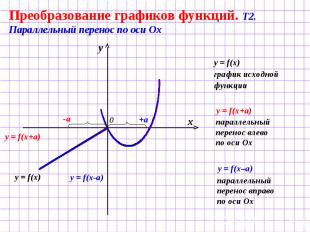
Преобразование графиков функций. Т2. Параллельный перенос по оси Ох y = f(x) график исходной функции параллельный перенос влево по оси Ох параллельный перенос вправо по оси Ох

Используя правила параллельного переноса вдоль координатных осей установите соответствие между формулой, задающей функцию и правилом преобразования ее графика. График данной функции построен путем параллельного переноса графика функции у = f(x) : - на 3 ед. вниз по оси Оу; - на 3 ед. вправо по Ох и на 3 вниз по Оу; - на 3 ед. вверх по оси Оу; - на 3 ед.влево по оси Ох и на 3 вниз по Оу; - на 3 ед. вправо по оси Ох; - на 3 ед. влево по оси Ох и на 3 вверх по Оу; - на 3 ед. вверх по оси Оу и на 3 вправо по Ох
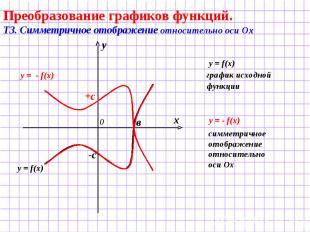
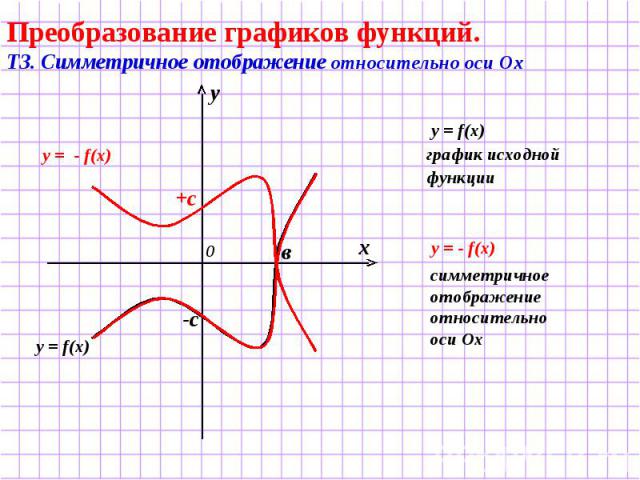
Преобразование графиков функций. Т3. Симметричное отображение относительно оси Ох y = f(x) график исходной функции симметричное отображение относительно оси Ох
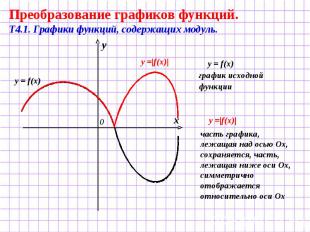
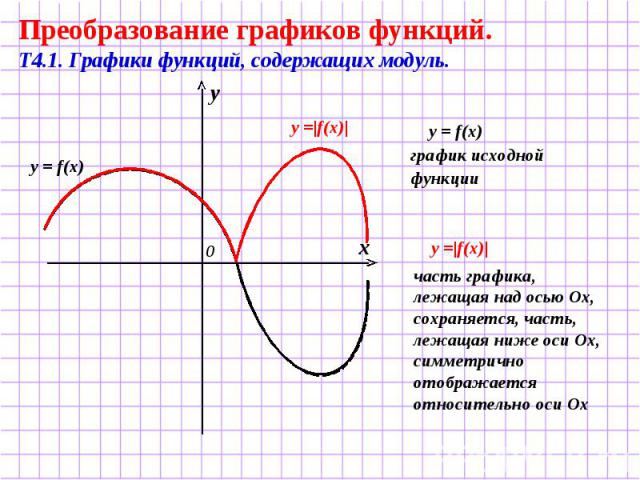
Преобразование графиков функций. Т4.1. Графики функций, содержащих модуль. y = f(x) график исходной функции часть графика, лежащая над осью Ох, сохраняется, часть, лежащая ниже оси Ох, симметрично отображается относительно оси Ох
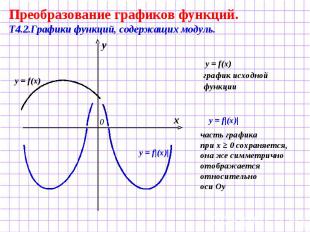
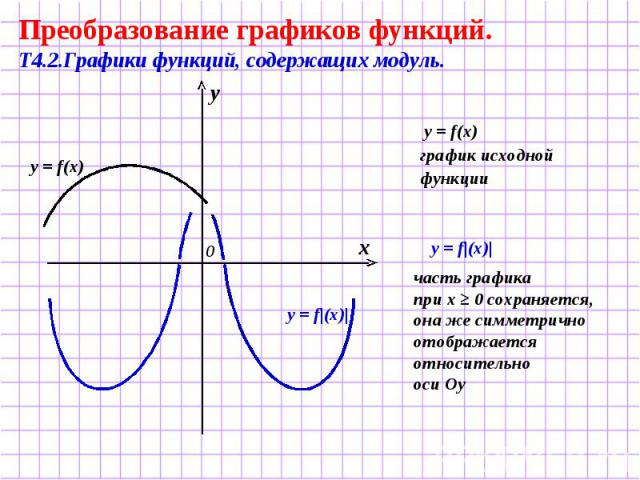
Преобразование графиков функций. Т4.2.Графики функций, содержащих модуль. y = f(x) график исходной функции часть графика при х ≥ 0 сохраняется, она же симметрично отображается относительно оси Оу
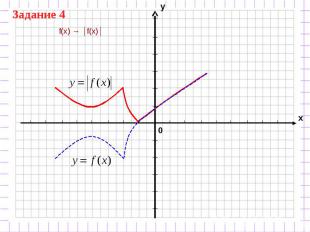
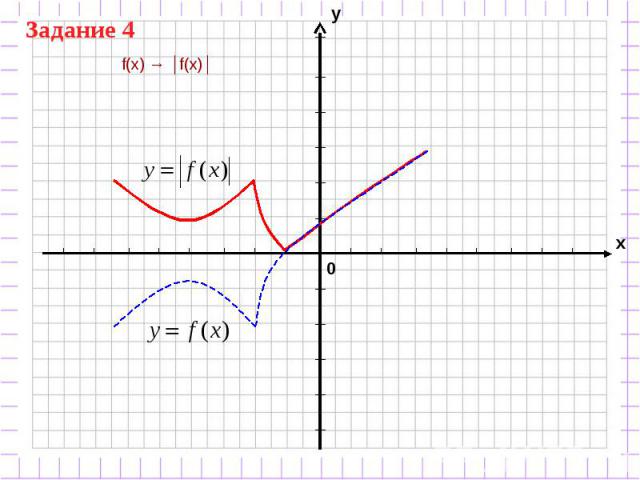
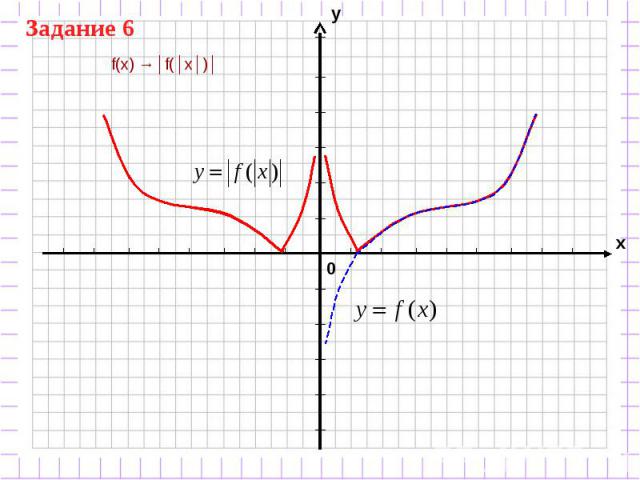
f(x) → │f(x)│
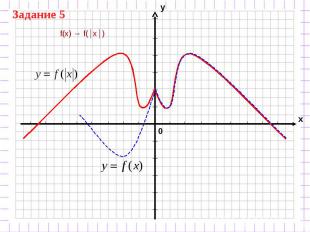
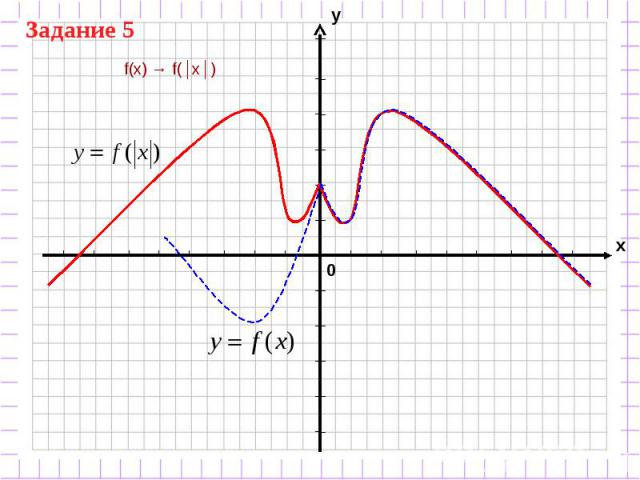
f(x) → f(│x│)
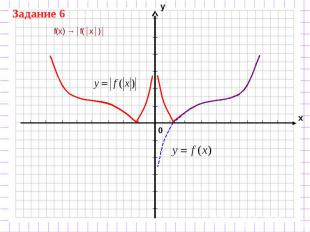
f(x) →│f(│x│)│

Домашнее задание: Используя правила преобразования графиков построить графики следующих функций: